深入理解PCM系统同步机制及其影响

1.以采用2PSK调制的PCM为例，说明三种同步在数字通信系统中的位置，并画出系统发送端和接收端的框图。

解：三种同步在数字通信系统中出现的前后顺序通常为载波同步、位同步和群同步。当数字系统采用2PSK调制、且假设载波同步和位同步均采用直接法时，发送端系统框图如图8-18所示，接收端系统框图如图8-19所示。

图8-18 PCM系统发送端框图

图8-19 PCM系统接收端框图

2.简述载波同步、位同步和群同步的应用。

解：（1）载波同步：只有相干解调才需要载波同步。因此，像AM、ASK及FSK的包络解调、2DPSK的相位比较法（差分相干解调）等非相干解调就不需要载波同步。此外，不经过调制的基带传输系统也不需要载波同步。

（2）位同步：凡是数字通信系统均需要位同步。因为，无论是数字基带系统还是数字频带系统，都需要经过取样判决才能恢复发送码元。

（3）群同步：将信息以分组形式传输的数字通信系统需要群同步。例如，PCM系统需要群同步，而△M系统则不需要群同步，因为在△M系统中，每个取样值只编一位二进制码元。

3.简述位同步脉冲信号与接收基带信号同频同相的含义。

解：当系统达到位同步时，位同步脉冲信号与接收基带信号同频同相。同频是指位同步脉冲信号的重复频率与发送码元的频率相同，这样才能做到每发送一个码元，接收端取样判决一次，恢复出一个码元，从而确保收、发码元个数相同。同相是指位定时脉冲应对准接收基带信号的最佳取样时刻。至于最佳取样时刻在何处，则取决于解调器的结构：对于低通滤波器型的解调器，最佳取样时刻在每个码元的正中间；若解调器采用匹配滤波器或相关器，则最佳取样时刻应在每个码元的结束点，因为这时的取样值幅度最大。图8-20a和图8-20b分别是低通滤波器和匹配滤波器（或相关器）时的输出基带信号及位定时脉冲信号的位置。

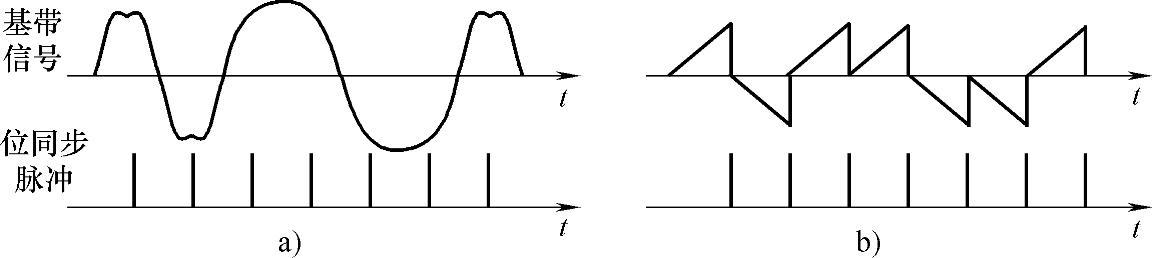
图8-20 位同步脉冲对准最佳取样时刻

4.试分析载波同步相位误差Δϕ对SSB解调性能的影响。

解：对于SSB信号，载波相位误差Δϕ不仅引起解调输出信噪比的下降，而且还会引起输出波形失真。

设单频基带信号为 m（t）=cosΩt

它对载波cosω_ct调制后的上边带信号为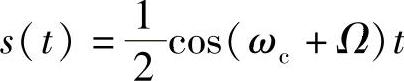

若接收端相干载波有相位误差Δϕ，则接收信号与之相乘后为

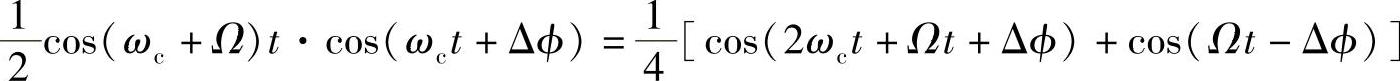
经低通滤波器后的解调输出为

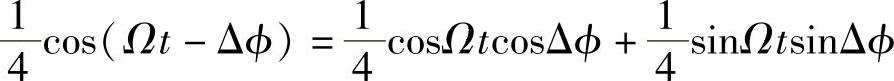
式中，第一项是原基带信号，受到因子cosΔϕ的衰减；第二项的存在使接收信号产生失真。可见，衰减和失真的程度随相位误差Δϕ的增大而增大。

5.相干解调器框图如图8-21所示。设输入为单边带信号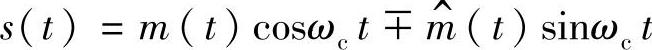，提取的相干载波为c_d（t）=cos[（ω_c+Δω）t+φ]，求解调器输出，并讨论载波同步的频差Δω和相差φ对解调性能的影响。

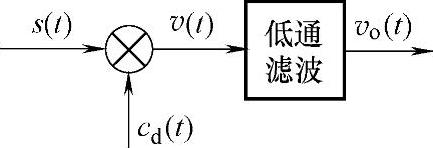
图8-21 相干解调器框图

解：由图可得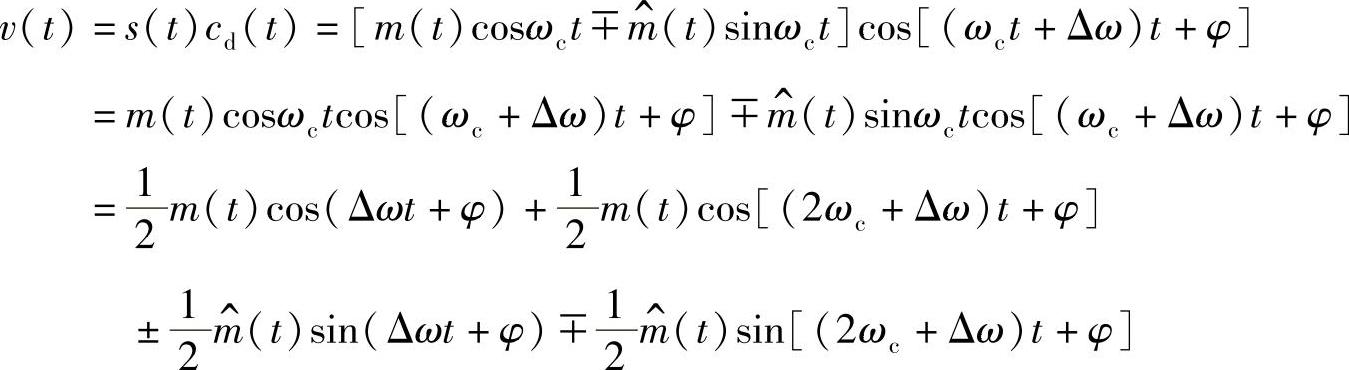

低通滤波器输出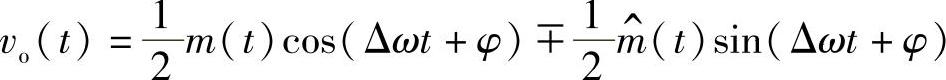

式中，第一项包含有用信号；第二项为干扰，使信号失真。

讨论：

●Δω=0、φ≠0时

①使有用信号幅度衰减cosφ倍。当φ不大时，影响不大。

②引入正交干扰项。仅当Δω=0、φ=0时，正交项不存在。

●Δω≠0、φ=0时

①对有用信号进行调制（乘以cosΔωt），引起有用信号畸变。

②引入受到调制的正交干扰项。

6.正交双边带（DSB）调制的原理框图如图8-22所示。若c（t）=cosω_ct，c_d（t）=cos（ω_ct+φ），试分析载波相位误差φ对解调输出的影响。

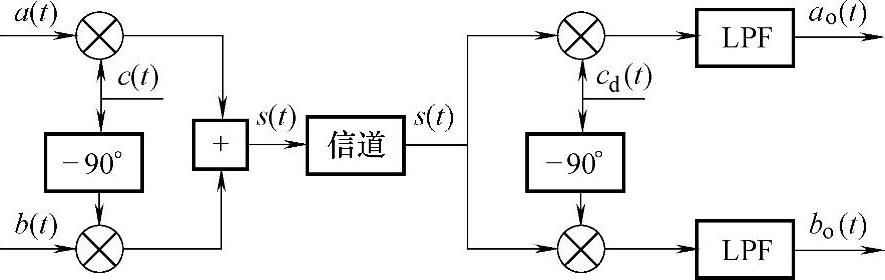
图8-22 正交DSB调制器框图

解：由图8-22可得 s（t）=a（t）cosω_ct+b（t）sinω_ct

解调时，上支路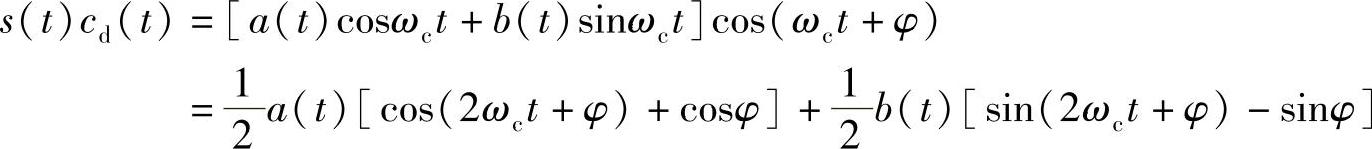

低通滤波后得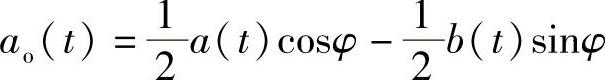

同理可得下支路的解调输出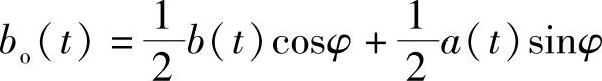

分析上支路解调输出发现，当载波相位误差φ≠0时，除了对有用信号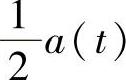衰减cosφ之外，还引入了与另一路信号b（t）有关的干扰项。

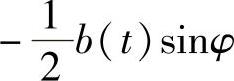下支路输出信号具有类似的结果。

归纳起来，载波相位误差φ对正交双边带信号解调的影响主要有：①使上、下两支路输出的有用信号衰减cosφ倍，即输出信噪比下降cos²φ倍。②使上、下两支路的信号互相干扰。

说明：

●正交DSB调制是利用正交载波在同一信道传输两路独立信号的技术。从前面的分析可以看出，当载波同步（即同频同相）时，两路信号在接收端可完全分离。

●若载波存在相位误差（无频差）时，会引起两路信号间的相互串扰，这与单路传输时不同。

●若载波存在频差，则输出信号的恶化将会更加严重。

7.试分析单边带信号能否用平方变换法提取相干载波。(www.xing528.com)

解：单边信号可表示为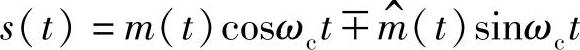

平方后为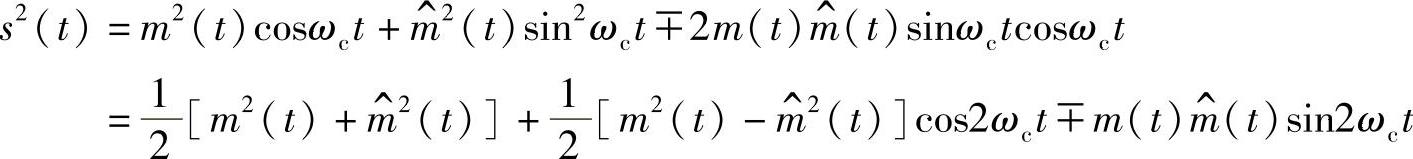

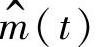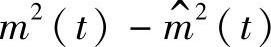由单边带信号和希尔伯特变换性质可知，m（t）、无直流，故及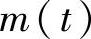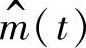项均不含有直流分量。因此，s²（t）中无2f_c分量，所以不能用平方变换法提取相干载波。

8.若给定5位巴克码组为01000，其中“1”取值+1，“0”取值-1。

（1）求出巴克码的局部自相关函数，并画出图形。

（2）若以此巴克码作为群同步码，画出相应的巴克码识别器。

解：（1）巴克码组a₁a₂a₃a₄a₅=-1+1-1-1-1，由局部自相关函数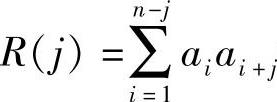得

当j=0时，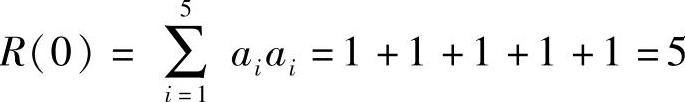

当j=1时，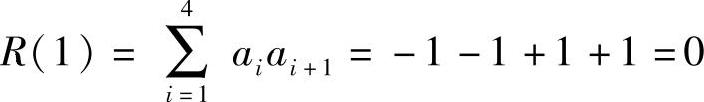

当j=2时，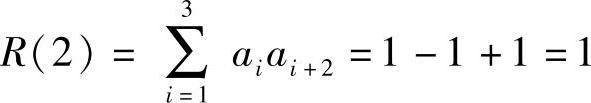

当j=3时，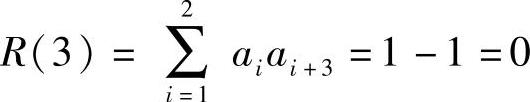

当j=4时，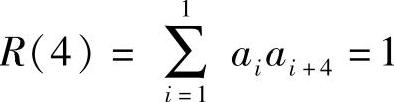

又因为自相关函数是偶函数，故局部自相关函数曲线如图8-23所示。

（2）巴克码识别器如图8-24所示。

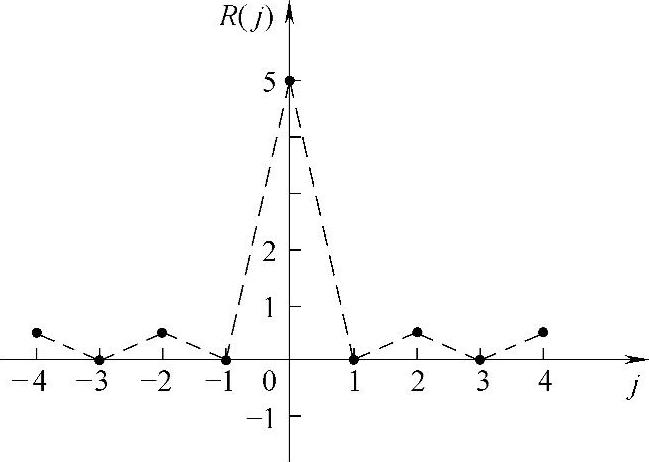
图8-23 局部自相关函数

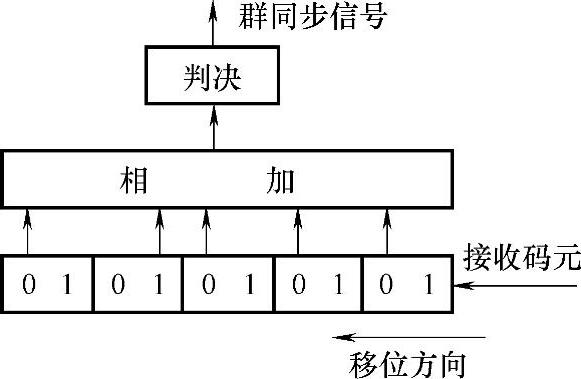
图8-24 巴克码识别器

9.A律PCM基群的偶帧同步码为0011011。

（1）画出该同步码的局部自相关函数曲线。

（2）画出此帧同步码的识别器原理图。

（3）分别求不允许错码、允许错一位码、允许错两位码时判决器的门限。

解：（1）参考题8解。该同步码的局部自相关函数曲线如图8-25所示。

（2）该帧同步码的识别器与7位巴克码识别器的画法相似，只是其中的移位寄存器的引出端与0011011相一致，如图8-26所示。

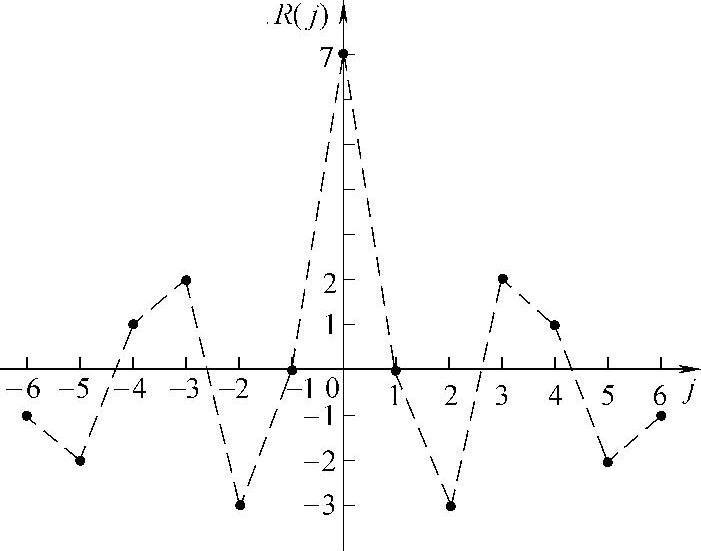
图8-25 帧同步码0011011局部自相关函数

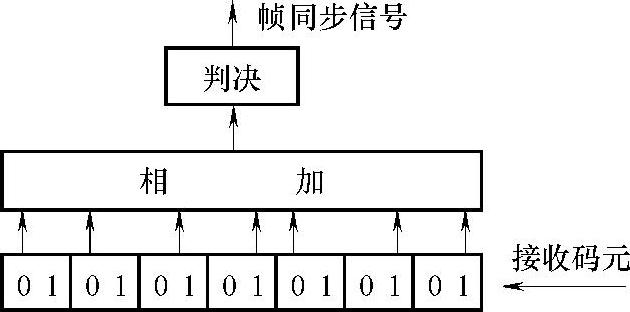
图8-26 帧同步码0011011识别器

（3）当一位都不错、错一位、错两位的同步码组通过识别器时，相加器输出分别为7、5和3。由此可见：

1）若不允许错码（m=0），判决门限可设为6。

2）若允许错一位码（m=1），判决门限可设为4。

3）若允许错两位码（m=2），判决门限可设为2。

10.设某数字通信系统中的群同步码为7位长的巴克码（1110010），采用连贯式插入法。

（1）画出群同步码识别器原理框图。

（2）若输入二进制序列为01011100111100100，画出群同步码识别器输出波形（设判决门限电平为4.5）。

（3）若码元错误概率P_e=2×10^-4，群同步码识别器判决门限电平为4.5，求识别器假同步概率。

解：（1）7位巴克码识别器原理图如图8-11所示。

（2）判决门限为4.5，表明同步码组出现一位错误时仍能检测出同步信号，因此识别器输出波形如图8-27所示。

图8-27 识别器输出波形（群同步信号）

（3）n=7，由判决门限4.5可知，m=1，故假同步概率为

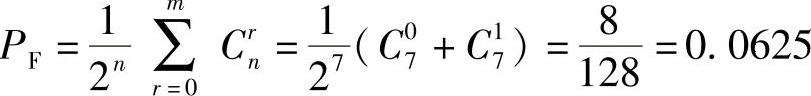
假同步概率与数字系统的误码率无关。

11.若7位巴克码的前后信息码元各有7个“1”，将它输入巴克码识别器，且识别器中各移位寄存器的初始状态均为“0”，试画出识别器的相加器输出波形和判决器输出波形。

解：若7位巴克码为“1110010”，则识别器如图8-11所示。

当“1”码元移入移位寄存器时，其“1”端输出电平为+1，“0”端输出电平为-1；反之，当“0”码移入时，其“1”端输出电平为-1，“0”端输出电平为+1。

又因为各移位寄存器的初始状态为“0”，因此，当第1个码元“1”输入时，最右边移位寄存器的输入为“1”，左边的6个移位寄存器相当于输入了“0”码，故接入到相加器的各输入端分别为（自左向右）-1-1-1+1+1-1-1，此时相加器输出为-3。依此方法，可计算出码元序列逐位经过识别器时相加器的输出。若判决器门限设置为6，则当7位巴克码全部移入时，相加器输出7，超过判决门限，则判决器输出一个脉冲。相加器输出及判决器输出的波形示意图如图8-28所示。

图8-28 识别器中相加器和判决器的输出波形