1.在△M和PCM两种数字化方法中,△M系统的取样频率比PCM系统的高得多,例如,对于语音信号的数字化,PCM的取样速率一般为8000次/s,而简单增量调制△M的取样速率至少为32000次/s。试对此给出解释。
解:△M系统的量化信噪比用分贝表示时的表达式近似为
(So/Nq)max≈(30lgfs-20lgf0-10lgfm-14)
为满足语音信号的正常通信,所需的量化信噪比需大于等于26dB,即要求
(30lgfs-20lgf0-10lgfm-14)≥26
上式是在单音(正弦波)信号时导出的,对于语音信号,可近似取f0=1000Hz,fm=3000Hz进行估算。进行简单运算后得
fs≥31.6kHz
即在△M系统中,对语音信号的取样频率需大于等于31.6kHz才能满足正常通信对量化信噪比的要求,这就是△M中对语音信号的取样频率通常为32kHz的原因。
2.已知模拟信号取样值的概率密度函数f(x)如图7-36所示。若按四电平进行均匀量化,试计算信号量化噪声功率比。
解:教材中推导均匀量化信噪比时假设信号是均匀分布的。本题给出的信号分布的概率密度函数为三角形,显然信号是非均匀分布的,故不能直接使用教材中的公式,应重新推导。
量化台阶为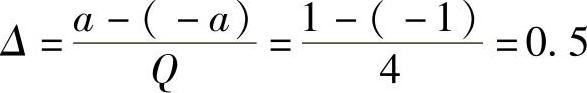
量化区间终点依次为:-1,-0.5,0,0.5,1
量化电平mi分别为:-0.75,-0.25,0.25,0.75
故量化特性如图7-37所示。
量化信号xq的功率为
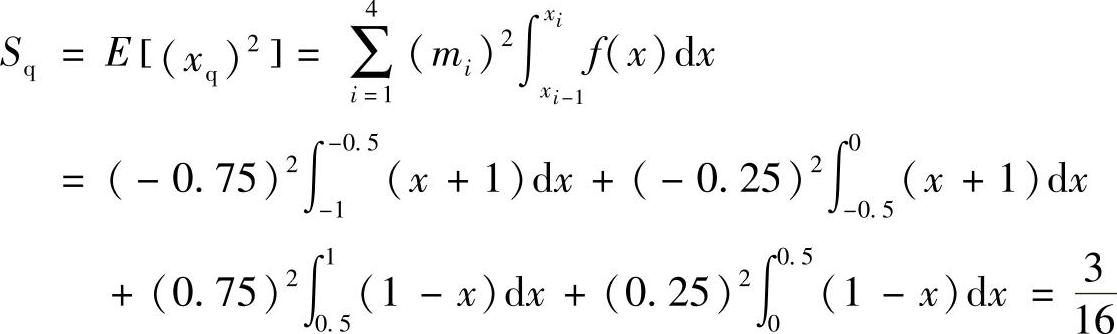
量化误差等于x-xq,其功率为
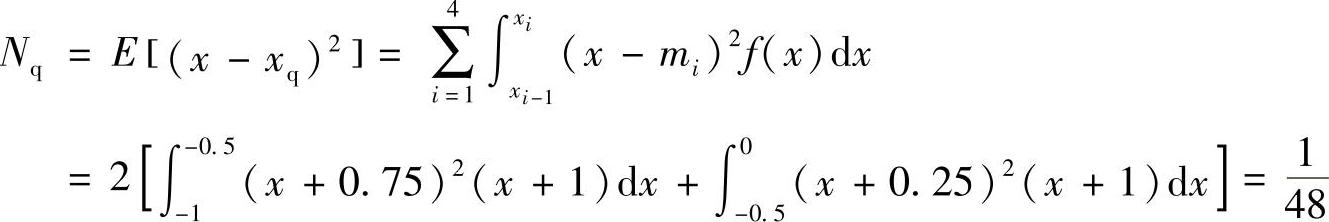
从而得量化信噪功率比为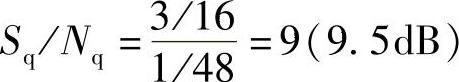
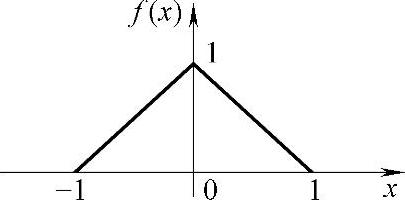
图7-36 模拟信号取样值的概率密度函数
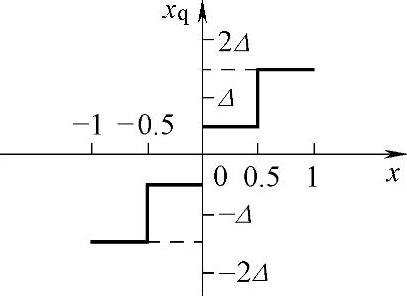
图7-37 量化特性
评注:通过本题,可掌握均匀量化信噪比分析的一般方法。
3.对语音信号的取样速率为8kHz。
(1)若采用PAM系统传输,脉冲占空比为1/3,求所需的传输带宽。
(2)若采用PCM系统传输,量化级数为128级,采用NRZ矩形脉冲,求所需的传输带宽。
解:(1)图7-3中,若用周期为Ts、占空比为1/3的矩形脉冲序列代替冲激脉冲序列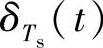 ,那么取样后的信号ms(t)即为占空比为1/3的PAM信号。矩形频谱的第一个零点即为此信号的带宽,故所需带宽为
,那么取样后的信号ms(t)即为占空比为1/3的PAM信号。矩形频谱的第一个零点即为此信号的带宽,故所需带宽为
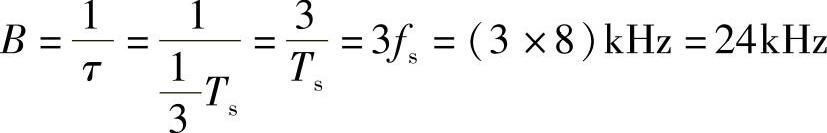
(2)已知Q=128,则k=log2Q=log2128=7,则二进制码元速率为
Rs=kfs=56kBaud
当采用不归零矩形脉冲波形时,此数字基带信号的带宽等于其功率谱的第一个零点,即等于其码元速率。故所需带宽为
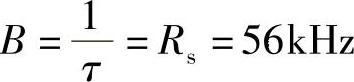
4.设单路语音信号m(t)的频率范围为200~3000Hz,取样频率为fs=8000次/s,将所得的取样值用PAM或PCM系统传输。
(1)计算PAM系统要求的最小信道带宽。
(2)在PCM系统中,取样值按128个量化电平进行二进制编码,PCM所要求的最小信道带宽是多大?
解:(1)取样后时间离散的样值序列即为PAM信号,故PAM信号的码元(一个样值看做一个码元)速率等于取样速率。所需的最小信道带宽等于码元速率的一半,即
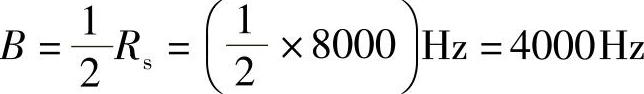
(2)由于Q=128,则k=log2Q=log2128=7,故PCM系统的二进制码元速率为
Rs=kfs=56kBaud
最小带宽为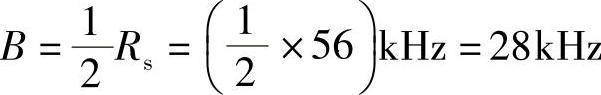
注意本题与第3题的区别:本题没有涉及信号的波形,因此可采用冲激脉冲,且系统为理想低通特性,此时频带利用率最高,所需信道带宽只有码元速率的一半。而第3题中,传输信号的波形采用矩形脉冲,故最小带宽等于数字基带信号功率谱的第一个零点,其数值等于矩形脉冲宽度的倒数。
5.对语音信号m(t)采用13折线A律进行量化和编码,设m(t)的频率范围为0~4kHz,取值范围为-6.4~6.4V,m(t)的一个取样值为-5.275V。
(1)求最小量化台阶Δ。
(2)求13折线编码器输出的PCM码组和量化误差。
(3)写出该码组对应的均匀量化12位码。
(4)若13折线编码器输出的码组采用QPSK调制传输,求此QPSK信号的带宽。
解:(1)由2048Δ=6.4V得到
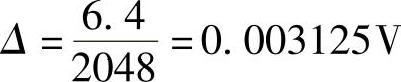
(2)取样值-5.275V用Δ表示时的大小为
(-5.275/6.4)×2048Δ=-1688Δ
由于
-1688Δ=-(1024Δ+64Δ×10+24Δ)
可见,此样点值位于负半轴的第8段、第11级,故样点值的PCM代码为01111010。
此代码代表负半轴第8段第11级的量化电平(量化级的中点电平)
-(1024Δ+64Δ×10+64Δ/2)=-1696Δ
因此量化误差绝对值为
1696Δ-1688Δ=8Δ=8×0.003125=0.025V
(3)均匀量化时,每个量化台阶的大小均为Δ,正负轴上共设置了4096个量化台阶,即量化台阶数Q=4096=212,故每个量化电平需要用12位二进制代码来表示。当采用折叠二进制码时(用0表示负取样值,其余11位以自然二进制方式表示电平的绝对大小),十进制数1688所对应的11位二进制数为
(1688)10=(11010011000)2
故其均匀量化所对应的12位二进制代码为011010011000。
(4)QPSK调制信号的带宽等于二进制信号的码元速率。由于13折线编码器输出的二进制信号的码元速率为
RB=kfs=(8×8000)Baud=64kBaud
可得QPSK信号的带宽为64kHz。
6.对语音信号m(t)按PCM编码传输,设m(t)的频率范围为0~4kHz,幅度的取值范围为-3.2~3.2V,对其进行均匀量化,且量化间隔为Δ=0.00625V。若对信号m(t)按奈奎斯特速率进行取样,试求下列情形下的码元传输速率。
(1)量化器输出信号直接进行传输。
(2)量化器输出信号按二进制传输。
(3)量化器输出信号按四进制传输。
解:(1)奈奎斯特取样速率等于低通信号最高频率的两倍,即
fs=2fH=2×4kHz=8kHz
每取样一次,量化器输出一个量化值,每个量化值即为一个码元。因此,量化器输出信号的码元速率等于取样速率,为(https://www.xing528.com)
Rs=fs=8000Baud
(2)若量化器的输出经二进制编码后再传输,则二进制码元速率等于取样速率fs乘以每个样点的二进制代码位数k。由信号的取值范围-3.2~3.2V和均匀量化台阶Δ=0.00625V可以求出量化电平数(量化台阶数)为
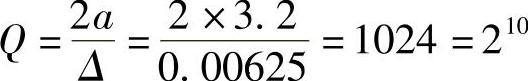
可见,每个样点要用k=10位的二进制代码来表示,故编码器输出的二进制码元速率为
Rs2=kfs=10×8000Baud=80kBaud
(3)将(2)中的二进制码元速率转换成四进制码元速率,即可得到量化器输出信号按四进制传输时的码元速率为
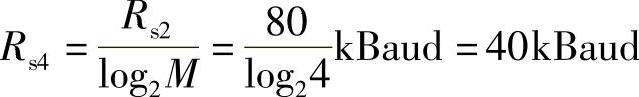
7.对输入正弦信号m(t)=Acos2πfkt分别进行PCM和增量调制编码。要求在PCM中采用均匀量化,量化级为Q,在增量调制中,量化台阶δ和取样速率fs的选择使信号不过载。
(1)分别求PCM和增量调制编码时的最小码元速率。
(2)若两者的码元速率相同,增量调制的量化台阶δ与信号振幅之间的关系如何?
解:(1)PCM系统的编码位数为 k=log2Q
最小取样速率等于信号最高频率的两倍 fsmin=2fk
故PCM编码后的最小二进制码元速率为 Rsmin=fsmin·k=2fk·log2Q
在增量调制中,由不过载的条件得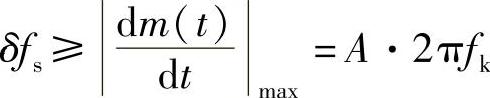
故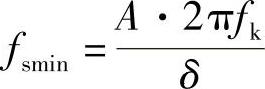 由于在增量调制中,每取样一次编码一位,故增量调制器输出的二进制码元序列的最小码元速率为
由于在增量调制中,每取样一次编码一位,故增量调制器输出的二进制码元序列的最小码元速率为
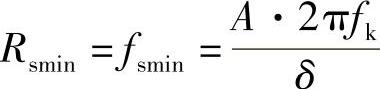
(2)当PCM与△M码元速率相同时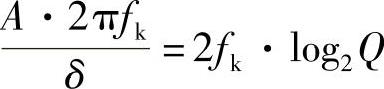
得到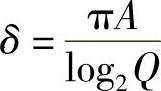
8.如图7-38所示,两路180kbit/s的数据和10路语音的PCM信号进行时分复用,合路后的数字信号经QPSK调制后在带通信道上传输。已知每路语音信号的取样速率为8000次/s,QPSK信号的功率谱主瓣宽度为1MHz,中心频率为400MHz。求语音信号数字化时采用的量化电平数Q。
解:本题是一道综合题,涉及PCM原理、时分复用后数据速率及数字调制QPSK的带宽问题。
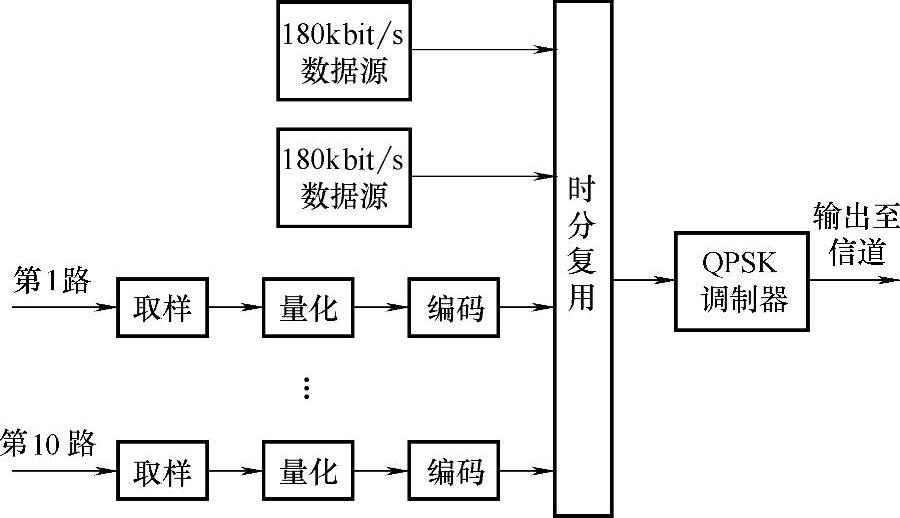
图7-38 信号调制和传输框图
由QPSK功率谱的主瓣宽度可知QPSK信号的带宽为1MHz,故调制前数字基带信号的信息速率应为
Rb=BQPSK=1Mbit/s=1000kbit/s
这是两路180kbit/s数据和10路语音PCM信号速率的总和,故一路语音信号的信息速率为
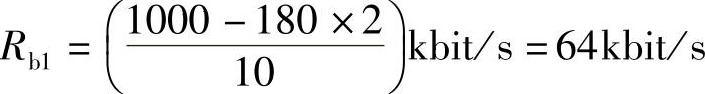
由Rb1=kfs,得64×103=k×8000,k=8,进而求得量化电平数为
Q=2k=28=256
9.若通信系统发射端框图如图7-39所示。设输入模拟信号的最高频率为4MHz,线性PCM系统采用奈奎斯特速率取样,量化电平数为256,余弦滚降系数为0.25。求
(1)线性PCM输出信号的信息速率Rb1。
(2)余弦滚降滤波器输出信号的信息速率Rb2和带宽Bb。
(3)若采用2PSK调制,求输出信号的码元速率和带宽(保持上述信息速率不变)。

图7-39 通信系统发射端框图
(4)若采用16QAM调制,求其输出信号的码元速率和带宽(保持信息速率不变)。
解:(1)已知信号的最高频率为fH=4MHz,且采用奈奎斯特取样,故取样速率为fs=2fH=2×4MHz=8MHz。又因为量化电平数Q=256,则k=log2Q=8。故PCM信号的二进制码元速率为
Rs=kfs=(8×8)MBaud=64MBaud
PCM信号的信息速率为
Rb1=Rslog2M=(64×log22)Mbit/s=64Mbit/s
(2)滚降前后的信号其信息速率保持不变,故
Rb2=Rb1=64Mbit/s
当信号为二进制时,其码元速率为64MBaud,通过余弦滚降成型后基带信号的带宽为
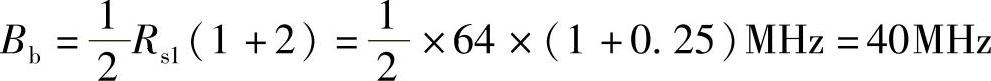
(3)2PSK信号的码元速率等于二进制基带信号的码元速率,即为
Rs2PSK=Rs=64MBaud
2PSK信号的带宽等于数字基带信号带宽的2倍,为
B2PSK=2Bb=2×40MHz=80MHz
(4)当信息速率为64Mbit/s时,十六进制信号的码元速率为
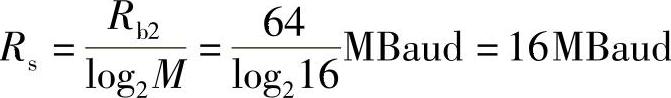
16QAM信号的码元速率等于十六进制数字基带信号的码元速率,即为Rs16QAM=16MBaud。成型后的基带信号的带宽为
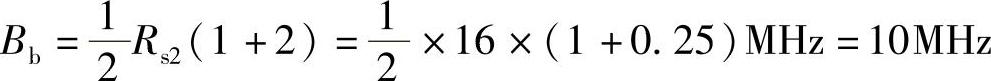
16QAM信号的带宽是基带信号的2倍,即为
B16QAM=2Bb=2×10MHz=20MHz
可见,16QAM信号的带宽是2PSK信号带宽的1/4,故16QAM调制的频带利用率是2PSK信号频带利用率的4倍。
10.简单增量调制(△M)系统的原理如图7-40所示。已知输入模拟信号m(t),以取样速率fs、量化台阶δ对m(t)进行简单增量调制,设初始量化电平为0。
(1)画出本地译码器输出m′(t),写出判决器输出Po(t)。
(2)若对24路△M信号进行时分复用,基带信号波形是占空比为50%的矩形,试求传输该基带信号所需的最小带宽。
(3)若24路基带信号的占空比为100%,采用16QAM方式传输,系统带宽取16QAM信号频谱的主瓣宽度,试求此时最大频带利用率为多少?
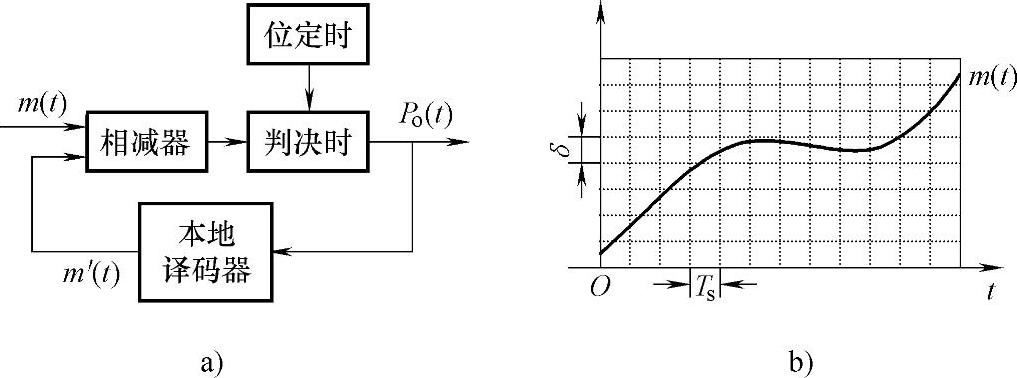
图7-40 △M系统原理
解:(1)本地译码器输出如图7-41所示。判决器输出Po(t)=111110101011…。
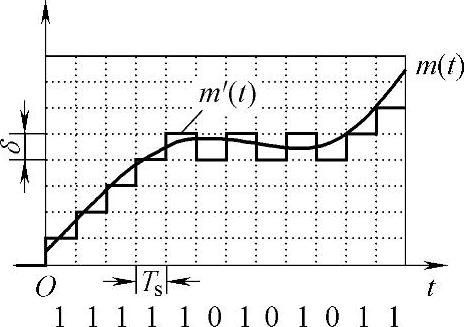
图7-41 本地译码器输出
(2)每路△M信号的二进制码元速率等于取样速率,即Rs1=fs,则24路△M复用后的二进制码元速率为Rs=24Rs1=24fs,码元宽度为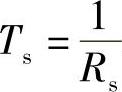 。当矩形脉冲的占空比为50%时,矩形脉冲宽度为
。当矩形脉冲的占空比为50%时,矩形脉冲宽度为
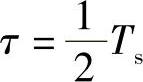
其第一个零点带宽为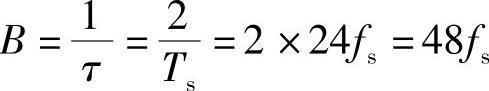
(3)M=16时,码元速率为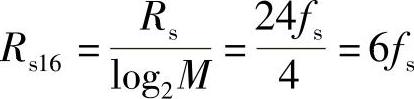 16QAM信号的带宽等于十六进制数字基带信号带宽的2倍,当采用全占空矩形脉冲时,数字基带信号的带宽等于其码元速率。因此,16QAM信号的带宽为
16QAM信号的带宽等于十六进制数字基带信号带宽的2倍,当采用全占空矩形脉冲时,数字基带信号的带宽等于其码元速率。因此,16QAM信号的带宽为
B16QAM=2×6fs=12fs
故16QAM信号的频带利用率为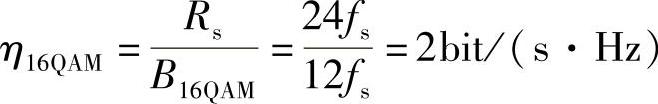
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




