求解理想低通滤波器的截止频率

1.一个带限低通信号m（t）具有如下的频谱特性：

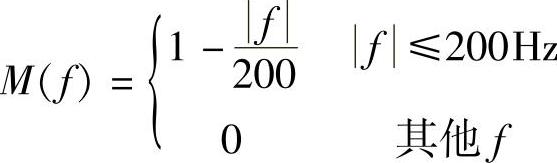
（1）若取样频率f_s=300Hz，画出对m（t）进行取样时，在f≤200Hz范围内已取样信号的频谱。

（2）f_s改为400Hz后重复步骤（1）。

解：由题意得模拟基带信号的频谱如图7-20所示。

（1）取样后信号的频谱是原信号频谱的周期重复，当取样频率为f_s=300Hz时，频谱的重复周期为300Hz，频谱如图7-21所示。

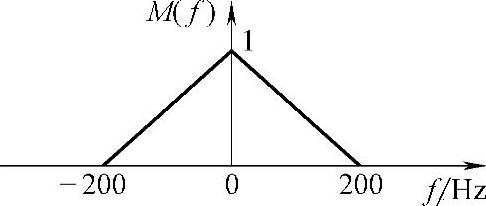
图7-20 模拟基带信号的频谱

图7-21 取样后的频谱

可见，由于取样频率太低，取样后的信号频谱有重叠。f≤200Hz内的频谱如图7-22所示。

（2）当取样频率为f_s=400Hz时，已取样信号的频谱如图7-23所示，重复频谱之间无重叠。

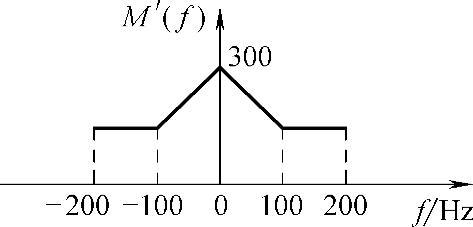
图7-22 f≤200Hz的频谱

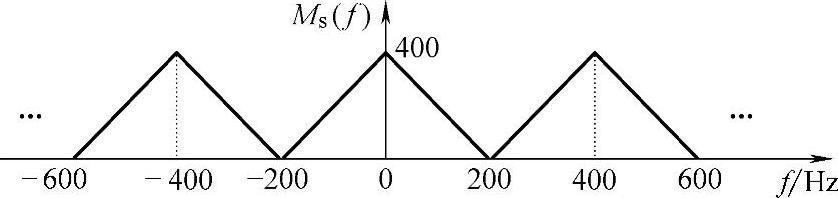
图7-23 f_s=400Hz的频谱

显然，f≤200Hz内的频谱如图7-24所示。

2.一个信号m（t）=2cos400πt+6cos4πt，用fs=500Hz的取样频率对它取样，取样后的信号经过一个截止频率为400Hz、幅度为1/500的理想低通滤波器。求

（1）低通滤波器输出端的频率成分。

（2）低通滤波器输出信号的时间表达式。

解：（1）m（t）的频率成分有两个，一个是2Hz，另一个是200Hz。其频谱如图7-25所示。

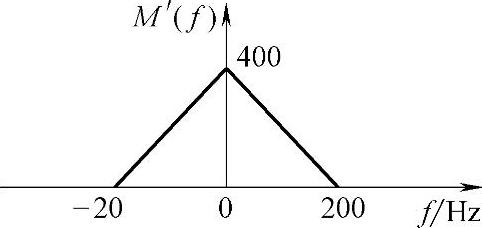
图7-24 f≤200Hz的频谱

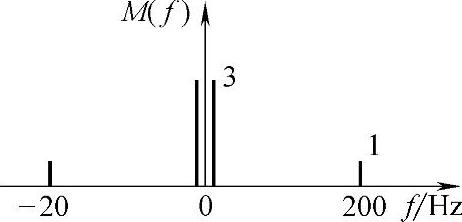
图7-25 频谱示意图

以500Hz的频率对其进行取样后，已取样信号的频谱如图7-26所示。

通过截止频率为400Hz的低通滤波器后，输出信号的频谱（低通滤波器的幅度为1/500）如图7-27所示。

图7-26 已取样信号的频谱

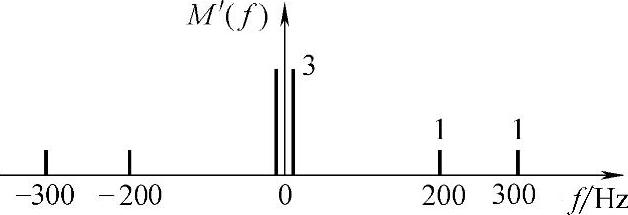
图7-27 输出信号的频谱

可见，低通滤波器输出端的频率成分有3个，分别是2Hz、200Hz和300Hz。幅度分别为6、2和2。

（2）由上面的分析可知，低通滤波器输出信号的时间表达式为

y（t）=2cos400πt+6cos4πt+2cos600πt

3.有信号m（t）=10cos20πtcos200πt，用250次/s的取样速率对其进行取样。

（1）画出已取样信号的频谱。

（2）求出用于恢复原信号的理想低通滤波器的截止频率。

解：利用三角公式得

m（t）=5（cos220πt+cos180πt）=5cos220πt+5cos180πt此信号含有两个频率成分，一个频率为110Hz，另一个频率为90Hz，幅度均为5。频谱如图7-28所示。

用250Hz对其进行取样后，频谱如图7-29所示。

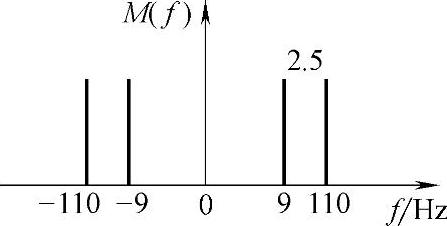
图7-28 频谱示意图

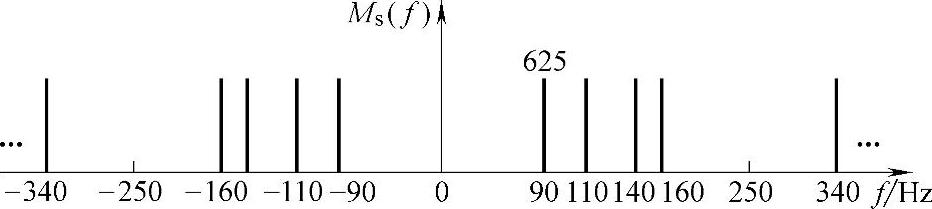
图7-29 取样后频谱

由上述频谱可见，要想从中恢复原信号的频谱，低通滤波器的截止频率应在110～140Hz之间，因此截止频率B的取值范围为110Hz＜B＜140Hz。

4.已知某信号的时域表达式为

m（t）=200Sa²（200πt）

对此信号进行取样。求

（1）奈奎斯特取样频率f_s。

（2）奈奎斯特取样间隔T_s。

（3）画出取样频率为500Hz时的已取样信号的频谱。

（4）当取样频率为500Hz时，画出恢复原信号的低通滤波器的传递特性H（f）示意图。

解：时域信号为取样函数的平方时，其频谱为三角形。再根据二者之间参数的对应关系，可得到，当信号时域表达式为m（t）=200Sa²（200πt）时，其频谱是截止频率为200Hz的三角形，如图7-30所示。

（1）由信号的最高频率可得奈奎斯特取样频率为f_s=400Hz。

（2）奈奎斯特取样间隔为T_s=1/f_s=1/400s=0.0025s。

（3）当取样频率为500Hz时，已取样信号的频谱如图7-31所示。

图7-30 频谱示意图

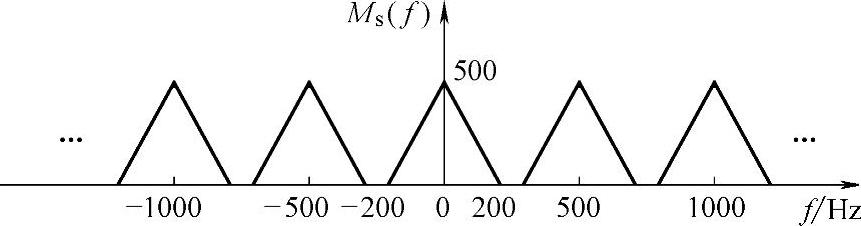
图7-31 取样后频谱

（4）要恢复原信号，低通滤波器的截止频率范围应为200～300Hz。其中一种的示意图如图7-32所示。

5.设单路语音信号m（t）的频率范围为300～3400Hz，取样频率为f_s=8kHz，量化级数Q=128。试求PCM信号的二进制码元速率为多少？

解：由Q=2^k可得，当Q=128时，k=7。所以PCM信号的二进制码元速率为

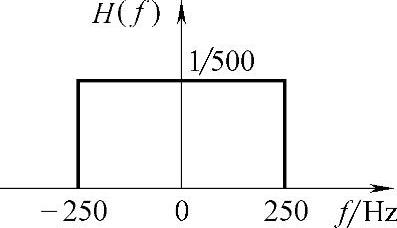
图7-32 低通滤波器示意图

R_s=kf_s=（7×8000）Baud=56000Baud=56kBaud

6.已知某13折线编码器输出样值为+785mV，若最小量化级为1mV，试求13折线编码器输出的码组。

解：由题意可知最小量化台阶Δ=1mV，所以用Δ表示的取样值的大小为

785mV=785Δ

（1）极性为正，得极性码x₁=1。(www.xing528.com)

（2）785Δ落在第7段，得段落码x₂x₃x₄=110。

（3）第7段的起始电平为512Δ，终止电平为1024Δ，此段被均分成16个量化级，每级大小为32Δ。由785Δ得

（785-512）÷32=8余17

可见落在第9级，其量化级码为x₅x₆x₇x₈=1000。

因此，785mV经13折线量化编码后的输出码组为11101000。

7.13折线编码，收到的码组为11101000，若最小量化级为1mV，求译码器输出电压值。

解：由接收到的码组11101000可知

（1）极性码为1，说明取样值为正。

（2）段落码为110，说明取样值落在第7段。

（3）段内量化级码为1000，说明取样值处于第9级。

译码器输出电平是代码所对应的量化电平，量化电平处于量化级的中间位置。所以代码11101000所对应的量化电平即译码器的输出电平值为

[512Δ+（9-1）×32Δ+32Δ/2]=784Δ=784mV

其中，512Δ是第7段的起始电平，32Δ是第7段中量化级的大小。

8.图7-33是一个对单极性模拟信号进行PCM编码后的输出波形。其最小量化电平为0.5V，量化台阶为1V，编码采用自然二进制码。图中正、负脉冲分别表示“1”码和“0”码。每3个码元组成一个PCM码组。试画出此PCM波形译码后的样值序列。

图7-33 对单极性模拟信号进行PCM编码后的输出波形

解：由波形图可见，PCM码元序列为：001010011100101110。每3位二进制码元为一个码组，码组序列为：001，010，011，100，101，110。码组与量化电平之间的对应关系如下：

码组 量化电平

000 0.5

001 1.5

010 2.5

011 3.5

100 4.5

101 5.5

110 6.5

111 7.5

因此，译码器输出样值序列为：1.5，2.5，3.5，4.5，5.5，6.5。波形图如图7-34所示。

9.设简单增量调制系统的量化台阶δ=50mV，取样频率为f_s=32kHz，求当输入信号为800Hz正弦波时，允许的最大振幅为多大？

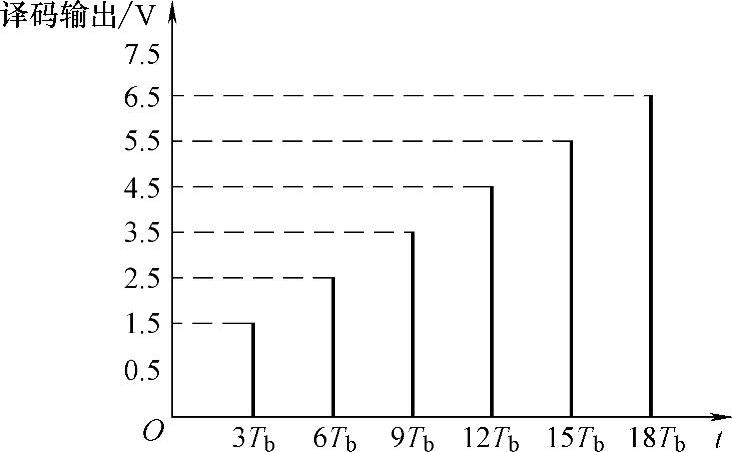
图7-34 译码器输出波形

解：设输入正弦波为m（t）=Acos1600πt，为保证不出现过载，必须满足

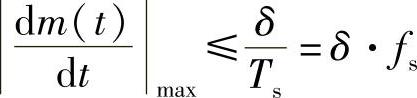
解得 A×1600π≤δ·fs

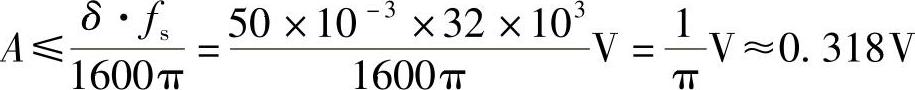
因此，允许的最大信号振幅为 A_max=0.318V

10.对信号m（t）=Asin2πf₀t进行简单增量调制，若台阶δ和取样频率的选择既要保证不过载，又要保证不致于因为信号振幅太小而使增量调制器不能正常编码，试证明此时要求f_s＞πf₀。

解：由不过载条件得

为保证正常编码，信号的幅度与台阶之间应有

2A＞δ

即 A＞δ/2 （7-28）

将式（7-28）代入式（7-27）得

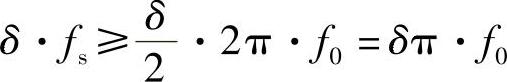
进一步解得f_s≥π·f₀

11.简单增量调制系统，已知输入模拟信号m（t）=Acos2πf₀t，取样速率为f_s，量化台阶为δ。

（1）试求简单增量调制的最大跟踪斜率k。

（2）若系统不出现过载失真且又能正常编码，则输入信号的幅度范围为多少？

（3）如果收到码序列为11011110001，请按阶梯信号方式画出译码器输出信号的波形（设初始电平为0）。

解：（1）最大跟踪斜率为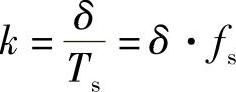

（2）由不过载条件得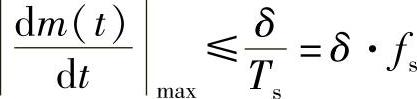

进一步解得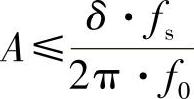

结合式（7-28）得输入信号的幅度范围为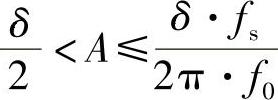

（3）增量调制译码器的工作是，收到一个“1”码，输出上升一个台阶，收到一个“0”码，输出下降一个台阶。故当译码器的输入序列为11011110001时，译码器输出信号的波形如图7-35所示。

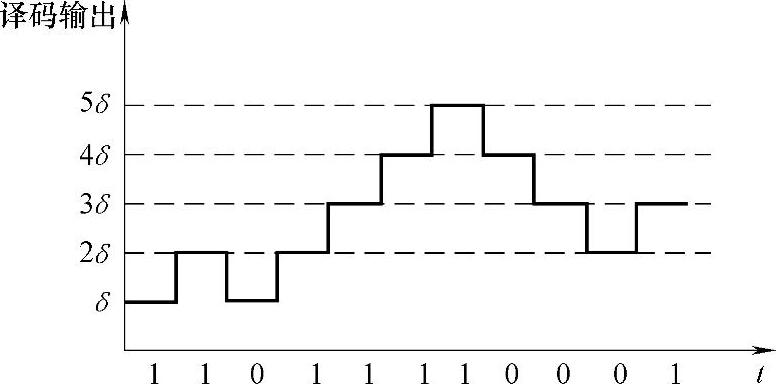
图7-35 译码器输出波形

12.24路语音信号进行时分复用并经PCM编码后在同一信道传输。每路语音信号的取样速率为f_s=8kHz，每个样点量化为256个量化电平中的一个，每个量化电平用8位二进制编码。求

（1）时分复用后PCM信号的二进制码元速率为多少？

（2）当用数字基带系统来传输此信号时，系统带宽最小为多少？

（3）当此数字信号经2PSK调制后再传输时，数字频带系统的带宽至少为多少？

解：（1）多路PCM时分复用后的二进制码元速率为

R_B=N·kf_s

式中，N为复用路数；kf_s是一路PCM的二进制码元速率；k与量化电平数Q之间的关系为Q=2^k。由Q=256得k=8。将k及f_s代入上式，得24路PCM复用信号的二进制码元速率为

R_B=N·kf_s=（24×8×8000）Baud=1536000Baud=1536kBaud

（2）当采用基带传输时，系统最小带宽为码元速率的一半，即为

B_min=768kHz

（3）当采用2PSK传输时，2PSK信号的带宽是数字基带信号码元速率的2倍，因此，2PSK信号的带宽为

B_2PSK=3072kHz

可见，数字频带系统的带宽至少为3072kHz。