PCM和△M的对比

1.编码原理

PCM和△M都是模拟信号数字化的具体方法。但PCM是对样值本身编码，其代码序列反映的是模拟信号的幅度信息；而△M是对相邻样值的差值编码，其代码序列反映了模拟信号的微分（变化）信息。

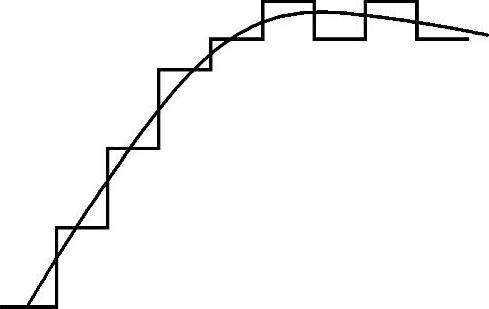
图7-16 自适应增量调制台阶变化示意图

2.取样速率

PCM的取样速率f_s是根据奈奎斯特取样定理来确定的。若信号的最高频率为f_H，则f_s≥2f_H。△M的取样速率比PCM的取样速率高很多。通常△M的取样速率f_s≥32kHz。

3.码元速率

以1路话音信号为例，数字化后的二进制码元速率为

PCM：R_s=kf_s=（8×8000）Baud=64kBaud（k=8，f_s=8kHz）

△M：R_s=kf_s=（1×32000）Baud=32kBaud（k=1，f_s=32kHz）

结论：△M的有效性高于PCM的有效性。

4.量化信噪比

比较的前提是数字化后的二进制码元速率相同，即有效性相同。

当信号为正弦信号时，PCM系统的量化信噪比公式为

（S_o/N_q）_PCM=（6k+2） （7-24）

码元速率为f_bPCM=8000k。(www.xing528.com)

△M系统的量化信噪比公式为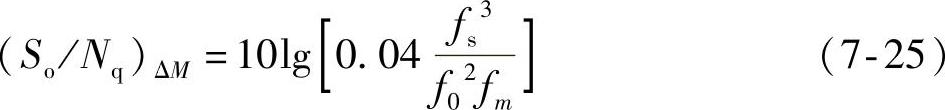

码元速率为f_bΔM=f_s。

当f_bΔM=f_bPCM时，f_s=8000k，同时取f₀=800Hz、f_m=3000Hz，代入式（7-25）得

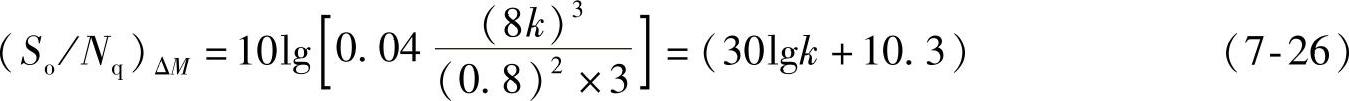
由式（7-24）和式（7-26）可计算出不同码元速率时PCM和ΔM的量化信噪比，如表7-2所示。

表7-2 不同k时两种数字化方法的量化信噪比

结论：

●当码位数k=4～5时，PCM和ΔM系统的量化性能相当。

●当k＜4，即码元速率小于32kBaud时，ΔM系统的量化性能好。

●当k＞5，即码元速率大于48kBaud时，PCM系统的量化性能好。

5.信道误码的影响

在ΔM系统中，每个误码只造成一个台阶的误差，所以对数字通信系统误码性能的要求较低，一般要求在10^-3～10^-4之间。而PCM的每个误码会造成较大的误差（可能有许多个台阶），所以对数字通信系统误码性能的要求较高，一般要求在10^-5～10^-6之间。

综上所述，PCM适用于要求传输质量较高、且具有丰富频带资源的场合，一般用于大容量的干线通信。ΔM由于有效性高、抗误码性能好等优点，主要用于一些专用通信网中。