如何提高拓展题的解析？

1.在实际的数字基带系统应用中，除了AMI码和HDB₃码外，有时还会碰到CMI码、双相码（曼彻斯特码）和密勒码等。CMI的编码规则为：信息为“0”码时用双比特“01”表示；信息为“1”码时，则交替地用“11”或“00”来表示。

（1）设信息为1110010100…，求相应的CMI码。

（2）以矩形全占空脉冲作为信号的波形，画出上述CMI码的波形图。

（3）设信息速率为1000Baud，则以矩形全占空脉冲为波形的CMI码信号的带宽为多少（第一个零点定义）？与相应的双极性全占空码信号相比，频带利用率如何变化？

解：（1）根据CMI的编码规则，信息1110010100…的CMI码如图5-24a所示。

（2）上述CMI码信号的波形图如图5-24b所示。

（3）在CMI码中，信息一个比特用CMI码的两个比特表示，故在CMI码中矩形宽度T_CMIb变为二进制信息比特宽度T_b的一半。因此，CMI码连续谱的主瓣宽度为比特速率的2倍，即CMI码的第一个零点带宽为

B_CMI=2R_b=2×1000Hz=2000Hz

相应的全占空双极性矩形信号的带宽在数值上等于二进制码元速率，即1000Hz。可见，CMI码的频带利用率下降了。

2.密勒码的编码与前一位有关，故又称为延迟调制码。

密勒码的编码规则：

●信息一个比特，密勒码用双比特表示。

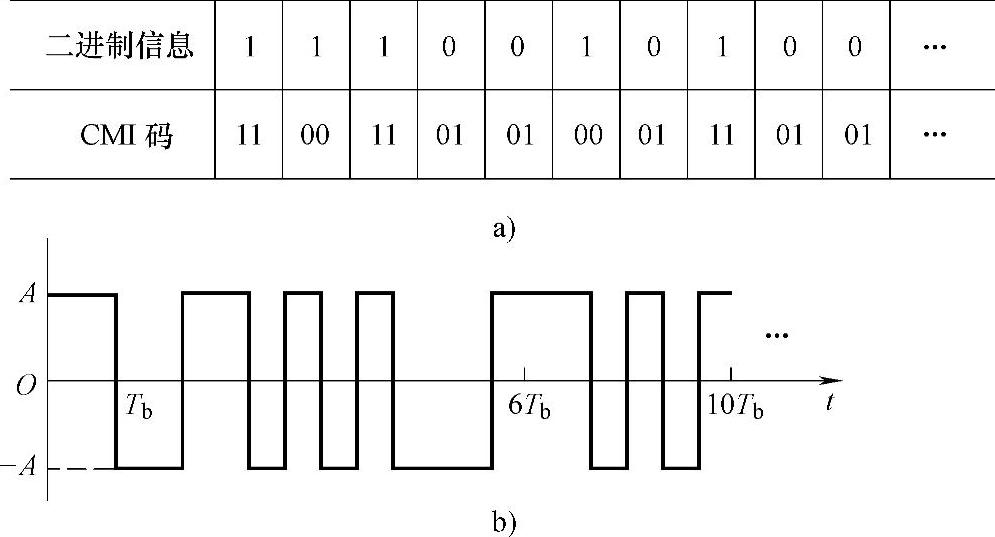
图5-24 CMI码及其波形

●信息“1”码，用01或10表示，到底用01还是10表示则要根据与之相邻的前一电平来确定。如前一电平为0，则用01，反之，如果前一电平为1，则用10。原则是使码元边界电平保持连续。故“1”码的编码规则简单概括为：码元边界连续，码元中点跃变。

●信息“0”码，用00或11表示。即码元中点不出现电平跃变。那么到底用00还是11呢？分两种情况：单个信息“0”码时，与前电平保持连续，如前一电平为0，则用00表示，反之，前一电平为1，则用11表示；信息中出现连“0”码时，在两个“0”码的边界处出现电平跃变，即00和11交替使用。

根据密勒码的编码规则，请完成：

（1）求信息序列10110001…的密勒码。

（2）以全占空矩形脉冲为波形画出上述密勒码波形图。

解：（1）根据密勒码编码规则得到的密勒码如图5-25a所示。

（2）波形图如图5-25b所示。

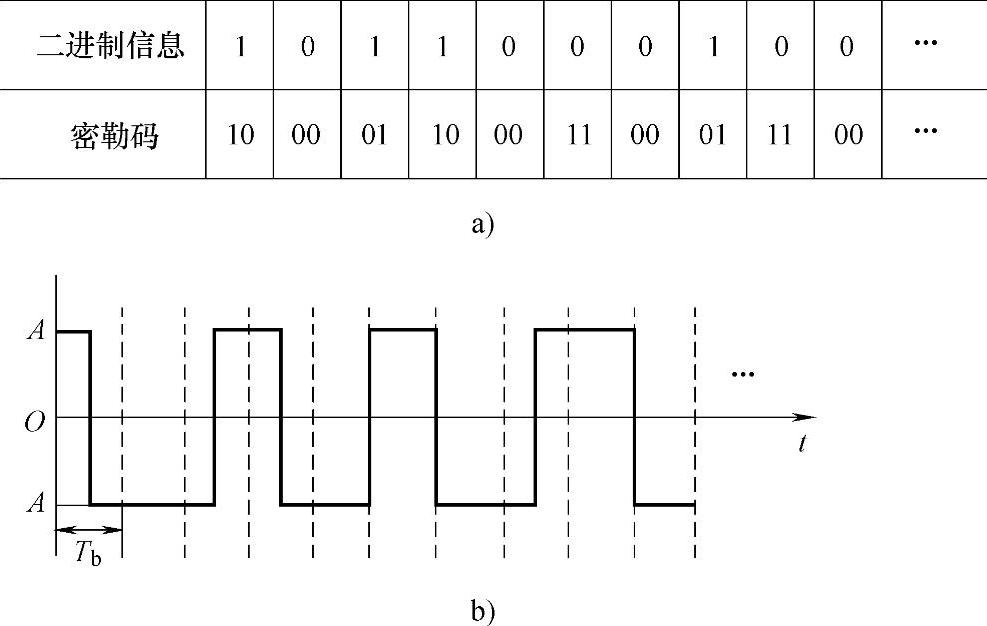
图5-25 密勒码及其波形

3.设有单极性二进制基带传输系统，“0”码和“1”码的概率分别为0.3和0.7，总传输特性为

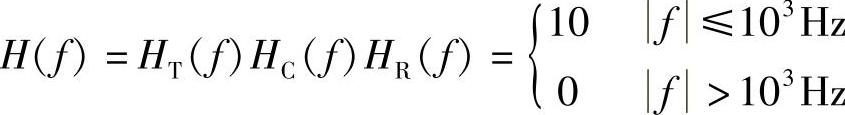
式中，H_C（f）=1，H_T（f）=H_R（f），信道噪声为n₀=10^-6W/Hz的零均值高斯白噪声，接收端取样时刻“1”码幅度为10V，“0”码幅度为0（不考虑码间干扰），求最佳判决门限和最小误码率。

解：（1）由式（5-8）可知，单极性系统的最佳判决门限电平表达式为

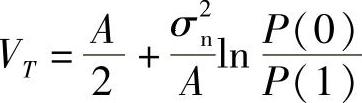
式中，A是发送“1”码时取样值中的信号电平；σ²_n是取样时刻噪声的平均功率。

接收滤波器输出端噪声功率谱密度为

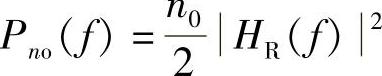
接收滤波器输出端即取样时刻噪声的平均功率为

且A=10V，故判决门限电平为

（2）发送“1”码时，取样值为

y=10+n

是个均值为A=10V、方差为σ²_n的高斯随机变量，因此其概率密度函数为

发送“0”码时，取样值为

y=n

是个均值为0、方差为σ²_n的高斯随机变量，其概率密度函数为

当判决规则为：y≥V_T判为“1”码，反之则判为“0”码时，最小误码率为

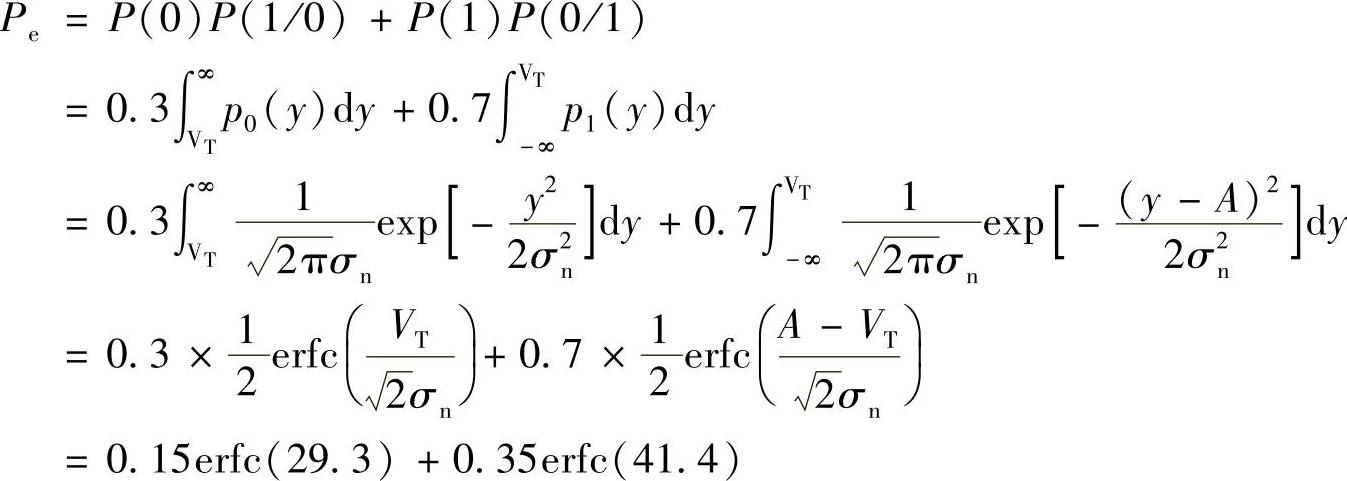
4.有4种基带传输系统的特性H（f）如图5-26所示，其中a、b为直线滚降，c、d为余弦滚降。试求

（1）无码间干扰时4种系统的最高码元速率和最高频带利用率。

（2）写出a、b两种系统的3种无码间干扰传输速率（从最大起）。

图5-26 4种基带传输系统的特性

解：（1）对于a、c传输特性，它们的等效低通特性的带宽相同，即

W_a=W_c=1kHz

故最大无码间速率为 R_s=2W_a=2W_c=2000Baud

两种特性的带宽相同，均为B=2kHz，故最大频带利用率为

对于b、d传输特性，它们的等效低通特性的带宽也相同，为

W_b=W_d=3kHz

故最大无码间速率为R_s=2W_b=2W_d=6000Baud

两种特性的带宽相同，均为B=4kHz，故b、d传输系统的最大频带利用率为

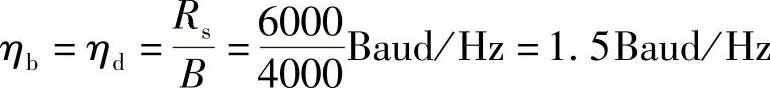
（2）由教材式（5-16）可知，滚降系统的无码间干扰传输速率为

故对于a特性，从最大开始的3个无码间干扰速率分别为

对于b传输特性，3个无码间干扰速率分别为

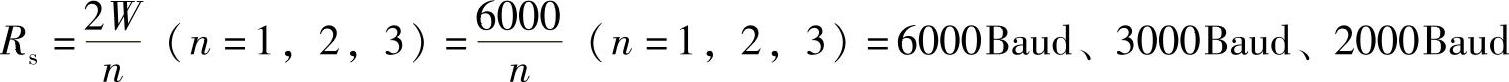
5.设有3种基带传输系统的特性，如图5-27中的a、b、c所示。

（1）3种系统在传输码元速率R_s=1000Baud的数字基带信号时，是否存在码间干扰？

（2）若无码间干扰，则频带利用率为多少？

（3）若取样时刻（位定时）存在偏差，哪种系统会引起较大的码间干扰？

（4）选用哪种系统更好？简要说明理由。

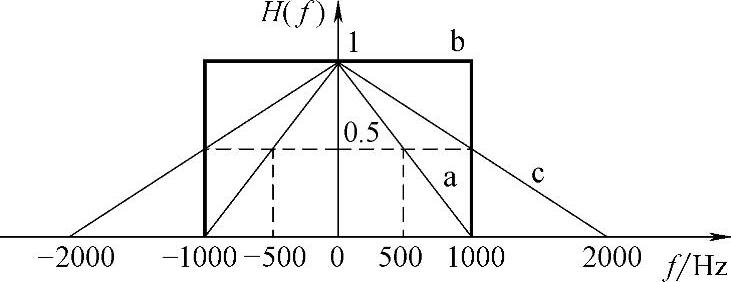
图5-27 3种基带传输系统的特性

解：（1）对于a传输特性，它的等效低通特性的带宽为

W_a=500Hz

故最大无码间速率为 R_s=2W_a=1000Baud

对于b传输特性，它是理想低通特性，其无码间干扰速率为等

对于c传输特性，其等效低通特性的带宽为

W_c=1000Hz

故无码间干扰速率有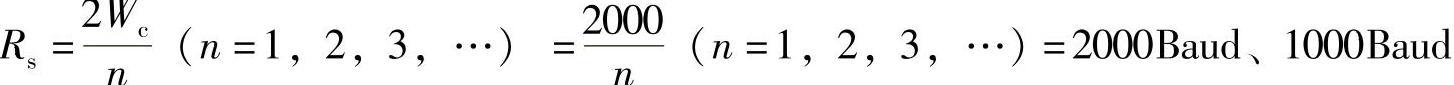等

可见，当传输速率为R_s=1000Baud时，上述3种系统均无码间干扰。

（2）由频带利用率公式，得3种系统的频带利用率分别为

a系统：

b系统：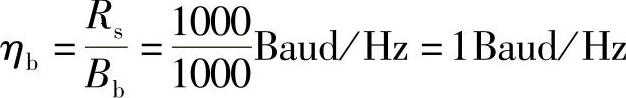

c系统：

其中B_a、B_b和B_c分别是3个系统的带宽。

（3）取样时刻偏差引起的码间干扰的大小取决于系统冲激响应“尾部”的收敛速率。“尾部”收敛速率越快，时间偏差引起的码间干扰就越小，反之则越大。

传输特性b是理想低通特性，其冲激响应为h_b（t）=2000Sa（2000πt），与时间t成反比，“尾部”收敛速率慢，故时间偏差会引起较大的码间干扰。

传输特性a和c是三角特性，通过查到三角频谱的傅里叶反变换，得到两种特性的冲激响应分别为

h_a（t）=1000Sa²（1000πt）

h_c（t）=2000Sa²（2000πt）可见，它们均与时间t²成反比，“尾部”收敛快，故时间偏差引起的码间干扰较小。

（4）选用何种特性的系统传输数字基带信号，需要考虑可实现性、频带利用率及定时偏差引起的码间干扰的大小。系统b是理想系统，难以实现；系统a和c都是物理可实现的，且位定时引起的码间干扰较小，但系统a的频带利用率较高，故选用系统a较好。

6.图5-28中，输入速率为R_b=9600bit/s的二进制信号，经串/并转换变成3个并行支路的二进制序列，再经D/A转换输出八进制矩形不归零脉冲序列，再经网孔均衡器变换成冲激脉冲序列，然后经滚降因子α=0.5的升余弦特性系统传输。

（1）D/A输出端信号的码元速率为多少？

（2）传输系统的带宽为多少？系统的频带利用率为多少？

图5-28 数字基带传输系数

解：（1）图5-28中的1/3串/并转换和D/A转换器将二进制矩形脉冲序列转换成了八进制矩形脉冲序列，故D/A输出端的码元的宽度为输入端二进制码元宽度的3倍，即

T_s=3T_b

由此可得，D/A输出端信号的码元速率为

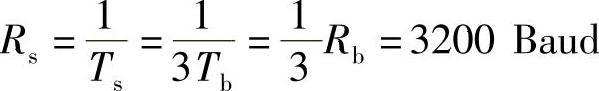
（2）由升余弦传输特性的滚降段中点（等效理想低通带宽）可求出最大无码间干扰传输速率。设升余弦滚降特性的滚降段的中点频率为W，则可传输的最大无码间干扰速率是W的2倍，即

R_s=2W

将码元速率R_s=32000Baud代入即可得W=1600Hz。再利用滚降特性带宽B与W及滚降系数α的关系就可求得

B=（1+α）W=（1+0.5）×1600Hz=2400Hz

系统的频带利用率为

7.二进制信息序列经MPAM调制（将二进制转换成M进制）及升余弦滤波后在基带信道中进行无码间干扰传输，信道带宽为3000Hz，若升余弦滤波器的滚降系数α分别为0、0.5、1。

（1）请分别求出系统无码间干扰基带传输的最大码元速率。

（2）若MPAM的M进制为16，请求出相应的二进制信息速率。

解：（1）对于具有滚降特性的系统，只要求出滚降的中心点频率W，最大无码间干扰速率即为W的2倍。

带宽B与中心点频率W及滚降系数α的关系式为B=（1+α）W，因此，故得

1）α=0时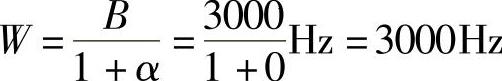，，最大无码间干扰速率R_s=2W=2×3000Baud=6000Baud。

2）α=0.5时，，最大无码间干扰速率R_s=2W=4000Baud。

3）α=1时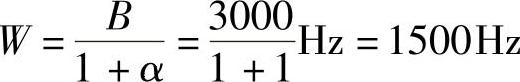，，最大无码间干扰速率R_s=2W=3000Baud。

（2）根据信息速率R_b与码元速率R_s之间的关系式R_b=R_s·logM，相应的信息速率分别为

1）α=0时，由于R_s=6000Baud，故R_b=（6000log₂16）bit/s=24000bit/s

2）α=0.5时，由于R_s=4000Baud，故R_b=（4000log₂16）bit/s=16000bit/s

3）α=1时，由于R_s=3000Baud，故R_b=（3000log₂16）bit/s=12000bit/s

8.已知二进制序列的“1”和“0”分别由s₁（t）和s₂（t）波形表示，“1”与“0”等概率出现。

s₁（t）=A 发“1”码 0≤t≤T_b

s₂（t）=0 发“0”码 0≤t≤T_b

在信道传输中受到加性白高斯噪声n_w（t）的干扰，加性噪声的均值为0、双边功率谱密度为，其接收机框图如图5-29所示。设信号通过低通滤波器的失真可忽略。

r（t）=s_i（t）+n_w（t） i=1或2 0≤t≤Tb

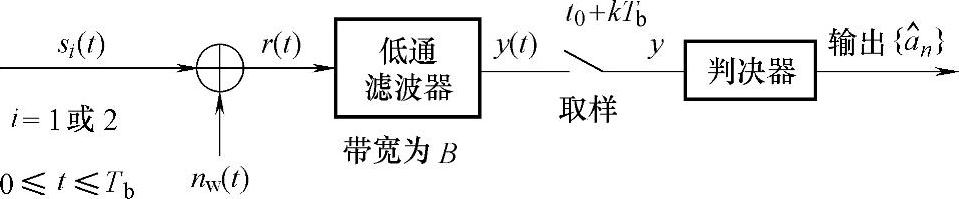
图5-29 二进制数字基带信号接收机框图

（1）若发送s₁（t），请

1）写出y（t）表达式。

2）求出取样值y的条件均值E（y/s₁）及条件方差D（y/s₁）。

3）写出y的条件概率密度函数p₁（y）。

（2）若发送s₂（t），请

1）写出y（t）表达式。

2）求出取样值y的条件均值E（y/s₂）及条件方差D（y/s₂）。

3）写出y的条件概率密度函数p₂（y）。

（3）画出p₁（y）及p₂（y）图。

（4）求最佳判决门限V_T值。

（5）详细推导出平均误比特率计算公式。

解：本题的解题过程实际上就是接收机误码率的推导过程及步骤。本题接收滤波器采用的是低通滤波器。

（1）当发送s₁（t）时

1）低通滤波器输出y（t）由信号和噪声两部分组成。由于信号波形通过低通滤波器的失真可忽略，因此，信号部分等于发送信号s₁（t）。噪声等于信道中的白噪声通过低通滤波器后的剩余（低通）噪声，用n_l（t）来表示，则低通滤波器输出y（t）表示为

y（t）=s₁（t）+n_l（t）=A+n_l（t） 0≤t≤T_b

2）在最佳取样时刻对y（t）取样得

y=A+n_l

式中，n_l是取样时刻噪声的瞬时值。由于n_l（t）是零均值高斯白噪声通过低通滤波器后的噪声，故有E[n_l（t）]=0、D[n_l（t）]=σ²_n=N₀B，所以y=A+n_l也是一个高斯随机变量，且均值和方差分别为

E[y/s₁]=E[A+n_l]=A

D[y/s₁]=D[A+n_l]=D[n_l]=N₀B

其中，B是低通滤波器的带宽。

3）根据前面的分析，当发送信号s₁（t）时，取样值y=A+n_l是均值为A、方差为N₀B的高斯随机变量，故其概率密度函数为

（2）当发送s₂（t）=0时

1）低通滤波器的输出y（t）表示为

y（t）=s₂（t）+n_l（t）=n_l（t） 0≤t≤T_b

2）对y（t）取样，取样值只有噪声的瞬时值，即

y=n_l

显然，此时y的条件均值和条件方差分别为

E[y/s₂]=E[n_l]=0

D[y/s₂]=D[n_l]=N₀B

3）y是均值为0、方差也为N₀B的高斯随机变量，其概率密度函数为

（3）p₁（y）及p₂（y）图形如图5-30所示。

图5-30 p₁（y）及p₂（y）图形

（4）由于1、0等概率，故最佳判决门限V_T应为两个取样值均值的平均，即

(www.xing528.com)

（5）概率密度函数及判决门限确定后，即可求出平均误比特率。判决规则为

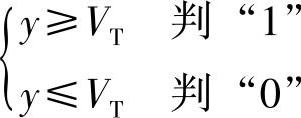
则发送“1”码时错判成“0”码的概率为

同样，发送“0”码时错判成“1”码的概率为

系统平均误比特率为

式中，A是发“1”时取样时刻的信号值；σ_n是噪声方差的平方根（零均值时噪声方差等于噪声功率）。此处推导结果与前面内容概要中给出的结论一致。

9.已知匹配滤波器型接收机框图及输入信号s_i（t）的波形如图5-31所示，s₁（t）与s₂（t）等概出现。信道中的噪声n_w（t）是零均值、功率谱密度为N₀/2的高斯白噪声。

（1）画出匹配滤波器冲激响应h（t）。

（2）若发送s₁（t），求出在t=T_b时刻取样的信号幅度值及瞬时信号功率、噪声平均功率。

（3）若发送s₂（t），求出在t=T_b时刻取样值y的条件均值E（y/s₂）及条件方差D（y/s₂），写出y的条件概率密度函数p₂（y）的表达式。

（4）推导出平均误比特率计算公式。

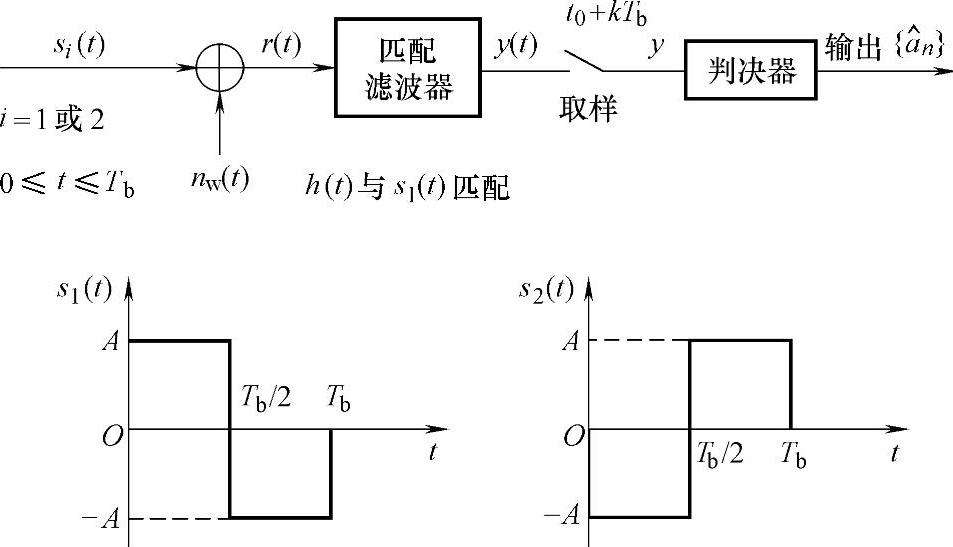
图5-31 匹配滤波器型接收机框图及输入信号波形

解：本题是接收滤波器采用匹配滤波器的最佳接收机的误码率推导过程。

（1）由匹配滤波器的特性可知，与信号s₁（t）匹配的匹配滤波器的冲激响应h（t）为

h（t）=s₁（t₀-t） 0≤t≤Tb

通常取t₀=T_b，因此h（t）的波形图如图5-32所示，是s₁（t）以纵坐标为对称轴进行折叠后再向右平移时间t₀=T_b。

图5-32 h（t）波形图

（2）若在0≤t≤T_b发送s₁（t），则接收信号为

r（t）=s₁（t）+n_w（t） 0≤t≤Tb

此时，匹配滤波器的输出y（t）为

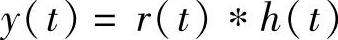
在t=T_b时刻对y（t）取样，得到的取样值y为

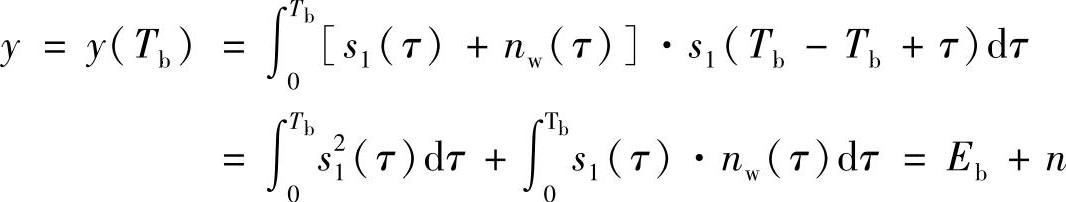
式中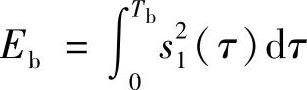，是接收滤波器输入端信号的比特能量，也是取样时刻信号的幅度值，故其瞬时功率为E_b²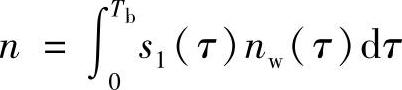；是取样时刻噪声的瞬时值，服从高斯分布，均值和方差分别为

（3）若在0≤t≤T_b发送s₂（t），则接收信号为

r（t）=s₂（t）+n_w（t） 0≤t≤T_b

此时，匹配滤波器的输出y（t）为

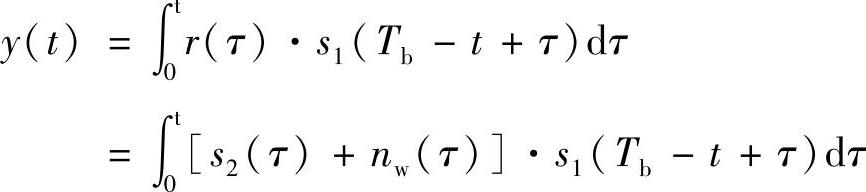
在t=T_b时刻对y（t）取样，得到的取样值y为

显然，y是高斯随机变量，其均值和方差分别为

故y的概率密度函数p₂（y）为

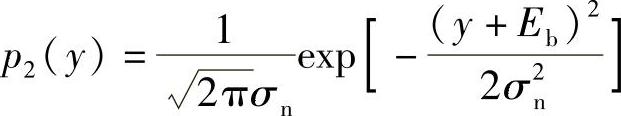
式中，。

（4）对于传输双极性信号，设发“1”码时，取样时刻信号的幅度为a（即取样值的均值），零均值噪声方差为σ²_n，发“0”码时，取样时刻信号的幅度值为-a。当“1”、“0”等概时，最佳判决门限电平为0，此时接收机误比特率为

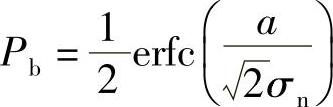
对于匹配滤波器型的接收机，取样判决时刻的信号幅度值及噪声功率与匹配滤波器输入端信号的比特能量及信道噪声功率谱密度之间的关系为（由上述推导结果）

a=Eb

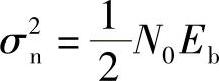
代入误比特率公式得到基带最佳接收机误比特率计算公式为

10.在理想带限及加性白高斯噪声干扰的信道条件下，最佳基带传输系统如图5-33所示。

图5-33 最佳基带传输系统

图中的发送滤波器、信道和接收滤波器的总传输特性为

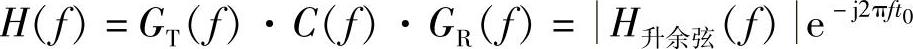
式中，C（f）是带宽为B、幅度为1的理想低通特性；接收滤波器的传输特性G_R（f）与发送滤波器的传输特性G_T（f）共轭匹配，即

G_T（f）、C（f）和G_R（f）在信道带宽内均为线性相移。

已知信道噪声是均值为0、功率谱密度为N₀/2的加性高斯白噪声，接收滤波器输入端的信号平均比特能量为E_b。

（1）请求出在最佳取样时刻取样值中的信号幅度值、瞬时信号功率及噪声平均功率、取样时刻取样值的信噪比。

（2）请推导出该系统的平均误比特率计算公式为

解：这是一个实际的数字基带系统模型。整个系统的H（f）具有升余弦传输特性，是个无码间干扰系统。而且，由题意可知，发“1”时接收码元的频谱为

R（f）=F[δ（t）]·G_T（f）·C（f）=G_T（f）

又已知接收滤波器的传输特性G_R（f）为

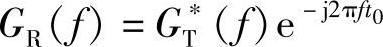
可见，接收滤波器与接收信号匹配，故接收机是最佳接收机。综合以上两点，框图5-33给出的基带系统是无码间干扰的最佳系统。

因为A点接收信号的平均能量E_b是已知参数，所以，本题所求结论均需用E_b来表示。为此，首先求出接收滤波器输入端的信号平均比特能量E_b与系统中其他参数的关系式。

根据题意且不失一般性，设升余弦传输特性的幅度为A，则本题中升余弦传输特性的表达式为

当发送信号是双极性信号时，发“1”码时的比特能量与发“0”码时的比特能量是相同的，因此，接收信号平均比特能量就等于发“1”码或发“0”码时的比特能量。以发送端发送“1”码为例，不考虑噪声时接收码元信号的频谱为

R（f）=F[δ（t）]·G_T（f）·C（f）=G_T（f）

根据帕塞瓦尔定理，接收码元能量（二进制码元能量即为比特能量）为

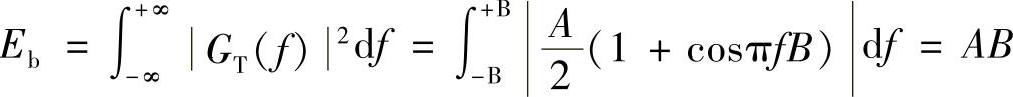
（1）由于发“1”和发“0”时的取样值是不同的，下面分两种情况讨论。

情况一 发“1”码即发送信号为δ（t）时：

不考虑噪声时，接收滤波器输出信号的频谱为

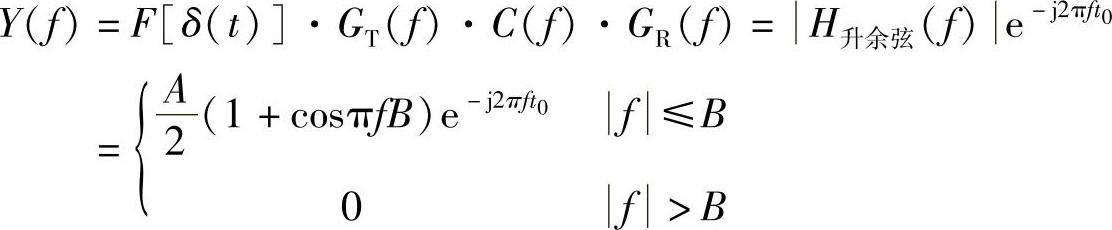
求其傅里叶反变换（查表得到升余弦频谱的冲激响应，再经t₀时延），得到接收滤波器输出端的信号为

由此可见，t₀时刻是最佳取样时刻，在此时刻取样能得到最大取样值。

1）最大取样值为AB=E_b。

2）瞬时信号功率为（AB）2=E²_b。

3）噪声平均功率为。求法如下：

先求出接收滤波器输出端的噪声功率谱为

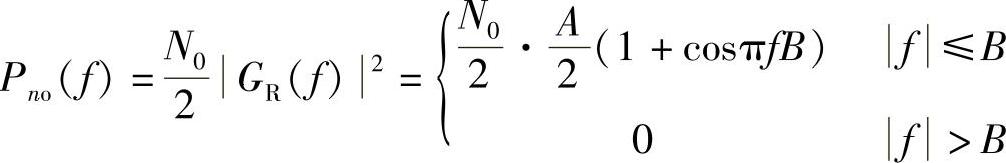
再对此功率谱求积分即可得到噪声功率为

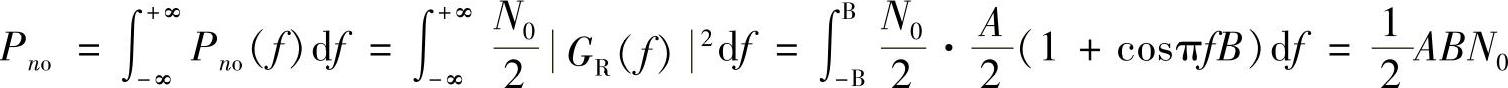
4）取样时刻的信噪比等于取样时刻的信号瞬时功率除以噪声平均功率，结果为

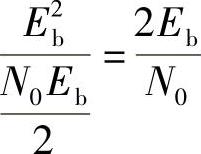
此结论与匹配滤波器内容中所得到的最大信噪比结论一致。

情况二 发“0”码即发送信号为-δ（t）时：

用与发“1”码时相同的演算过程，得到相关结果如下：

1）最大取样值为-AB=-E_b。

2）瞬时信号功率为（-AB）2=E²_b。

3）噪声平均功率为。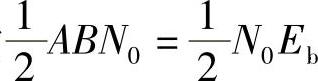

4）取样时刻的信噪比为。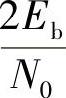

（2）当考虑噪声时，设取样判决时刻的接收信号为

y=a+n 发“1”码

y=-a+n 发“0”码

式中，a是取样时刻信号的瞬时幅度；n为取样时刻噪声的瞬时值。设取样时刻噪声的平均功率为σ²_n，则根据式（5-7），当“1”、“0”等概且判决门限电平为0时，系统的平均误比特率为

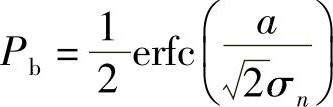
由（1）小题结果得a=E_b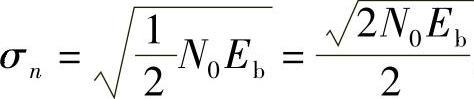，，代入上式得到用比特能量E_b和噪声功率谱密度N₀表示的系统平均误比特为

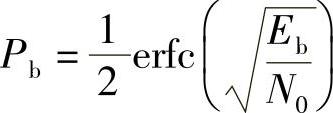
可见，得到了与第9题相同的结果，进一步证实了图5-33所示接收机是最佳的。

11.某基带传输系统，在取样时刻的取样值为y，y=a+n+i_m。其中a的取值为等概率的+1、-1。n是均值为0、方差为σ²的高斯随机变量。i_m是取样时刻的码间干扰，i_m有3个可能值：，0，，它们的出现概率分别为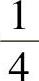，，。求该系统的平均误比特率计算公式。

解：本题是取样判决时刻有码间干扰的误码率推导过程。

本题给定系统为等概的双极性系统，最佳判决门限为发“1”和发“0”时取样值数学期望的均值。

发“1”时，E[y]=E[+1+n+i_m]=1+E[n]+E[i_m]=1

发“0”时，E[y]=E[-1+n+i_m]=-1+E[n]+E[i_m]=-1

故判决门限电平为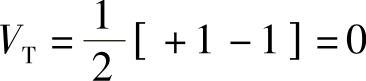，判决规则应为

V_T≥0，判“1”码

V_T≤0，判“0”码

系统误比特率计算方法为P_b=P（1）P（0/1）+P（0）P（1/0），下面分别计算P（0/1）和P（1/0）。

（1）发送“1”时，码间干扰的可能值有3种。

1）码间干扰取值时

E[y]=E[+1+n-1/2]=0.5+E[n]=0.5

D[y]=E[+1+n-1/2]=D[n]=σ²

可见，y是均值为0.5、方差为σ²的高斯随机变量，其概率密度函数为

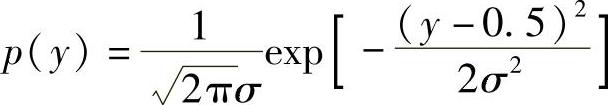
错判概率为

2）码间干扰取值为0时

E[y]=E[+1+n]=1+E[n]=1

D[y]=E[+1+n]=D[n]=σ²

由此可知，y是均值为1、方差为σ²的高斯随机变量，其概率密度函数为

错判概率为

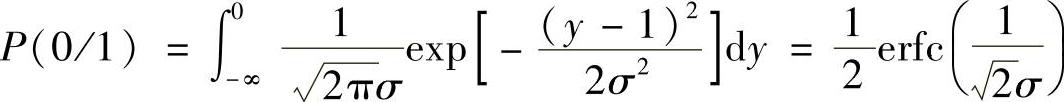
3）码间干扰取值时

E[y]=E[+1+n+1/2]=1.5+E[n]=1.5

D[y]=E[+1+n+1/2]=D[n]=σ²

所以，y是均值为1.5、方差为σ²的高斯随机变量，其概率密度函数为

错判概率为

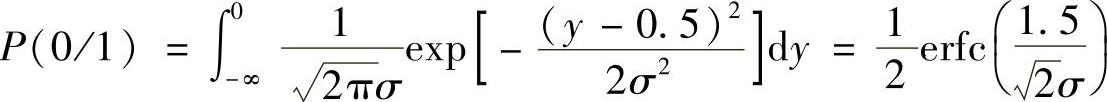
综合上述，发送“1”码时，发生错判的平均概率为

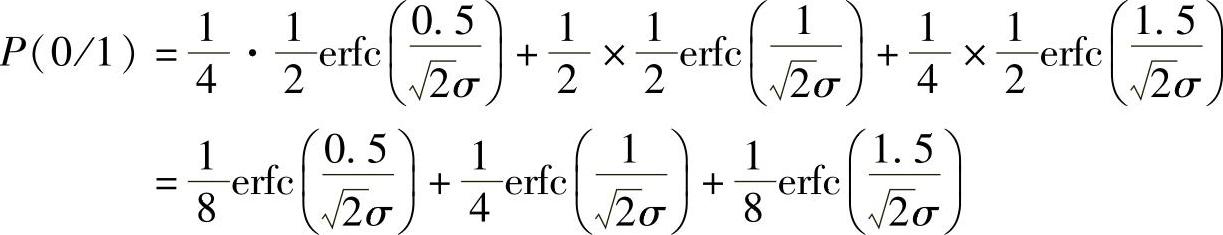
（2）发送“0”码时，根据码间干扰的不同取值，也分3种情况求解，方法与上面相同。

1）码间干扰取值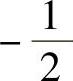时

E[y]=E[-1+n-1/2]=-1.5+E[n]=-1.5

D[y]=E[+1+n-1/2]=D[n]=σ²

y是均值为-1.5、方差为σ²的高斯随机变量，其概率密度函数为

错判概率为

2）码间干扰值为0时，E[y]=E[-1+n]=-1+E[n]=-1

D[y]=E[+1+n]=D[n]=σ²

y是均值为-1、方差为σ²的高斯随机变量，其概率密度函数为

错判概率为

3）码间干扰取值时

E[y]=E[-1+n+1/2]=-0.5+E[n]=-0.5

D[y]=E[+1+n+1/2]=D[n]=σ²

y是均值为-0.5、方差为σ²的高斯随机变量，其概率密度函数为

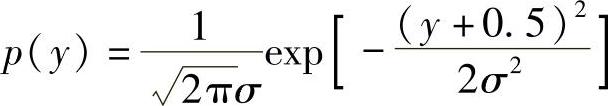
错判概率为

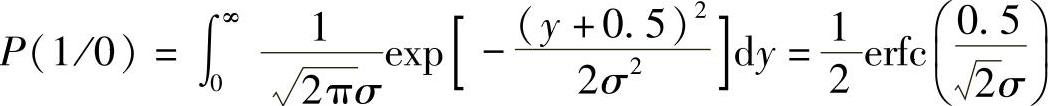
故发送“0”码时，发生错判的概率为

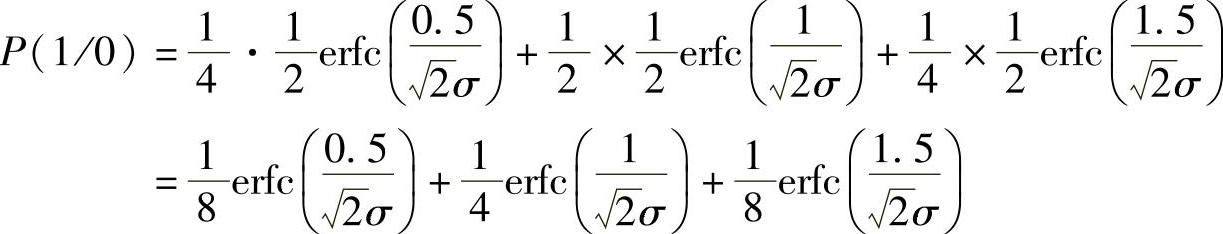
可见，P（0/1）=P（1/0），且“1”、“0”等概，所以系统平均误比特率为