1.已知二元信息序列为10011000001100000101,画出它所对应的单极性归零码、双极性全占空码、AMI码、HDB3码的波形图(基本波形用矩形)。
解:(1)单极性码:+100+1+100000+1+100000+10+1,如图5-13a所示。
(2)双极性码:+1-1-1+1+1-1-1-1-1-1+1+1-1-1-1-1-1+1-1+1,如图5-13b所示。
(3)AMI码:+100-1+100000-1+100000-10+1。用全占空矩形表示的AMI波形如图5-13c所示(第一个“1”码也可用负极性)。
(4)第一个特殊序列选用“100V”,第一位信息采用“+1”时的编码过程如下:
原信息序列: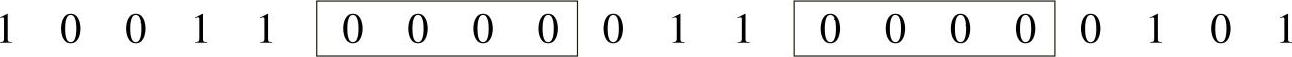
破坏长连零: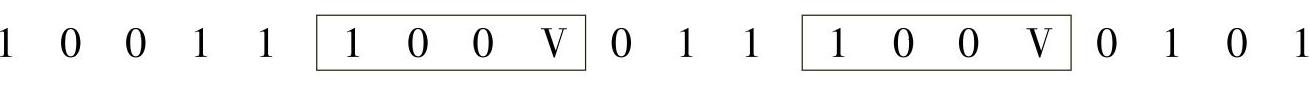
标上极性:+H 0 0-1+1 -H 0 0-H 0+1 -1 +1 0 0+V 0-1 0+1
用全占空矩形表示的波形如图5-13d所示。
2.已知HDB3码波形如图5-14所示,求原基带信息。
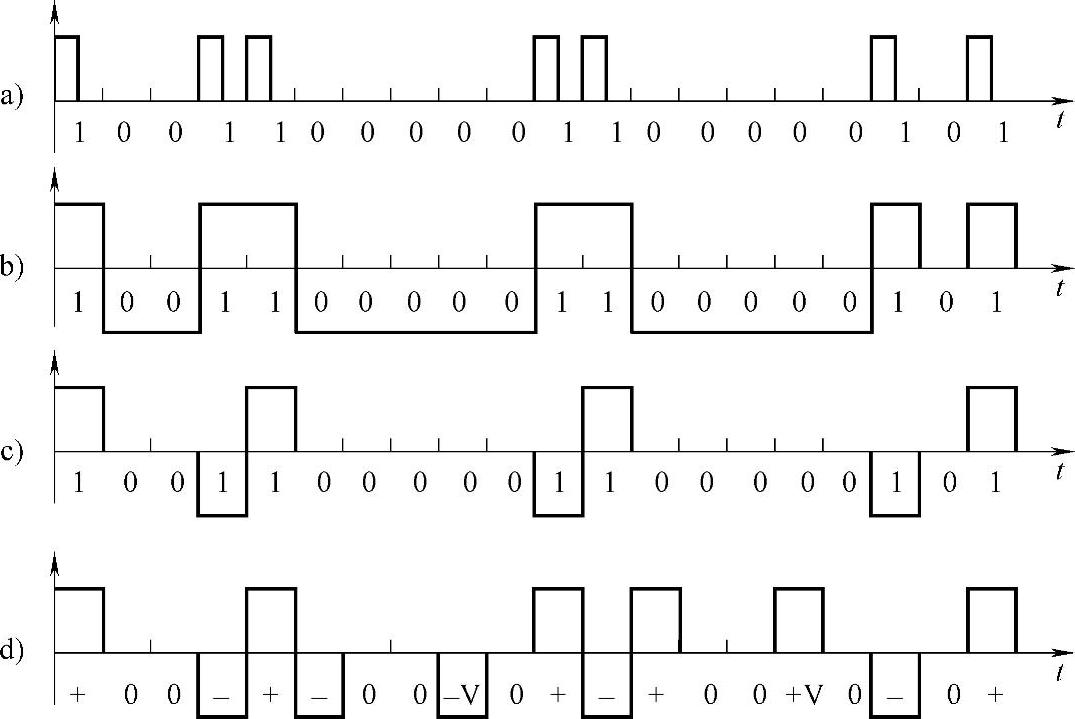
图5-13 用全占空矩形表示的波形

图5-14 HDB3码波形
解:本题涉及HDB3码的译码问题,可分两步进行。
1)找出V码,将V码与其前三位码(100V或000V)恢复成原信息0000。根据编码规则,HDB3码中如果出现连续两个同极性脉冲,这两个同极性脉冲中的后一脉冲则为V码,如图5-15所示。

图5-15 V码示意图
2)将正脉冲和负脉冲均恢复成“1”码,零电平(无脉冲)恢复成“0”码,得译码后的信息序列为101100001100000000。
3.试求出16位全0码、16位全1码及32位循环码的HDB3码(32位循环码为111011000111110011010010000001010)。
解:HDB3码编码的具体过程请参见教材中例题和题1解,这里不再重复。下面给出的HDB3码基于第一个4连0用1000V代替,第一个“1”码用正极性。
1)16位全0码的HDB3码:+100+1-100-1+100+1-100-1。
2)16位全1码的HDB3码:+1-1+1-1+1-1+1-1+1-1+1-1+1-1+1-1。
3)32位循环码的HDB3码:+1-1+10-1+1000-1+1-1+1-100+1-10+100-1+100+100-10+10。
需要注意:如果信息中连0个数不超过3个,则其HDB3码和AMI码相同。
4.已知一个以升余弦脉冲为基础的全占空双极性二进制随机脉冲序列,“1”码和“0”码分别为正、负升余弦脉冲,其宽度为Tb,幅度为2V,“1”码概率为0.6,“0”码概率为0.4。
(1)画出该随机序列功率谱示意图(标出频率轴上的关键参数)。
(2)求该随机序列的直流电压幅度。
(3)能否从该随机序列中提取1/Tb频率成分?
(4)求该随机序列的带宽。
解:由已知条件可得“1”码波形如图5-16所示。故“1”码波形的频谱为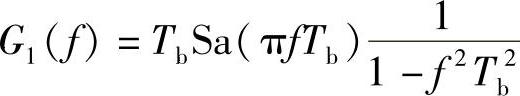 ,又由于“0”码波形g2(t)=-g1(t),因此得到
,又由于“0”码波形g2(t)=-g1(t),因此得到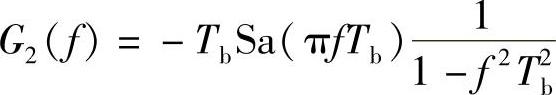 。
。
将“1”码、“0”码波形的频谱及它们的概率代入双边功率谱公式,得到
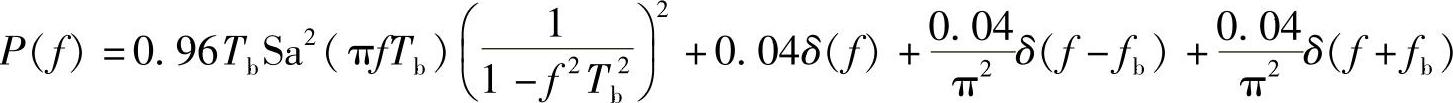
其中fb=1/Tb。
(1)由上述功率谱表达式可知,功率谱的连续谱最大值为0.96Tb,形状由升余弦脉冲频谱的平方决定,功率谱中只有直流分量谱和位定时分量谱两种离散谱,因此功率谱如图5-17所示。
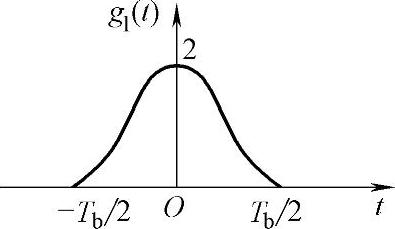
图5-16 “1”码波形
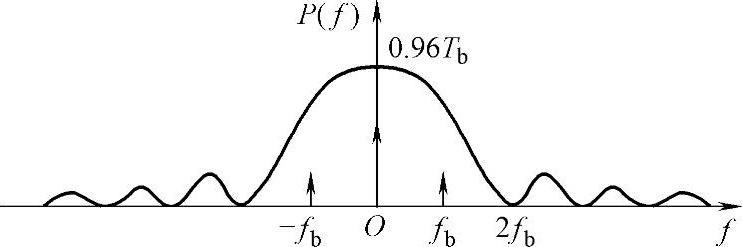
图5-17 功率谱
(2)由功率谱公式得直流功率谱为0.04δ(f),因此可得直流功率为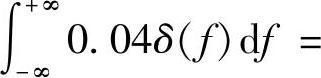
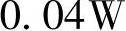 ,故直流电压为0.2V。
,故直流电压为0.2V。
(3)由于功率谱中含有1/Tb=fb的成分,所以能够从此信号中直接提取位定时信号。
(4)功率谱第一个零点在2/Tb=2fb处,所以此随机序列的第一个零点带宽为2/Tb,即等于二进制码元速率的2倍。
5.已知矩形、升余弦传输特性如图5-18所示。当采用以下速率传输时,指出哪些无码间干扰,哪些会引起码间干扰。

图5-18 矩形、升余弦传输特性
(1)Rs=1000 Baud (2)Rs=2000 Baud
(3)Rs=1500 Baud (4)Rs=3000 Baud
解:(1)理想低通滤波器的带宽为1000Hz,此系统所有的无码间干扰速率有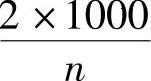
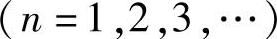 ,当n=1、2时得无码间干扰速率分别为2000Baud和1000Baud。所以这两个速率无码间干扰,1500Baud和3000Baud则有码间干扰。
,当n=1、2时得无码间干扰速率分别为2000Baud和1000Baud。所以这两个速率无码间干扰,1500Baud和3000Baud则有码间干扰。
(2)当升余弦特性的带宽为2000Hz时,其所有无码间干扰速率为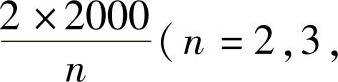
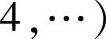 ,故2000Baud和1000Baud是无码间干扰的,而1500Baud和3000Baud则有码间干扰。(https://www.xing528.com)
,故2000Baud和1000Baud是无码间干扰的,而1500Baud和3000Baud则有码间干扰。(https://www.xing528.com)
6.设二进制基带系统的传输特性为
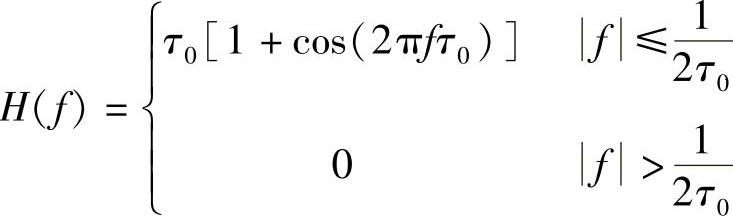
试确定系统最高无码间干扰传输速率及相应的码元间隔Tb。
解:将传输特性的曲线画出来,如图5-19所示。
由图5-19可见,此传输特性为升余弦,且带宽为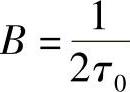 ,故最大无码间干扰速率为
,故最大无码间干扰速率为
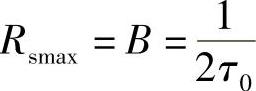
所对应的最小码元间隔为
Tb=1/Rsmax=2τ0
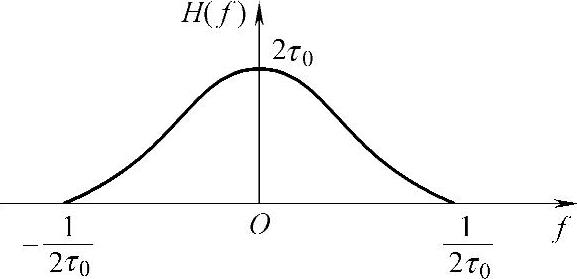
图5-19 传输特性
说明:二进制系统的码元间隔与比特间隔相同,故二进制系统中也常用Tb表示码元间隔。
7.已知某二进制数字基带系统,取样判决时刻信号电压的绝对值为0.8V,噪声的方差σ2n=20mW,试分别求传输单极性码和双极性码时系统的误码率。
解:由题已知a=0.8V,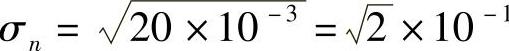 。
。
代入式(5-9),得单极性码时系统的误码率为
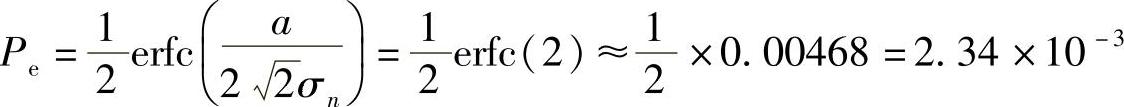
代入式(5-7),可得双极性码时系统的误码率为
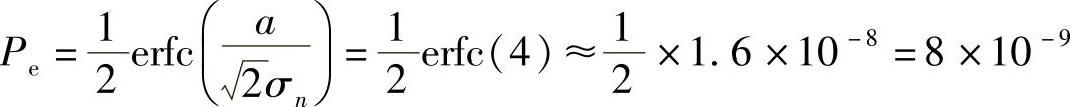
8.已知二进制数字基带系统的码元速率为2.5×106Baud,信道中加性高斯白噪声的功率谱密度n0/2=5×10-16W/Hz,接收端矩形脉冲信号的幅度为0.1mV。
(1)求系统传输单极性信号时的误码率。
(2)求系统传输双极性信号时的误码率。
解:已知A=0.1mV=0.1×10-3V=1×10-4V,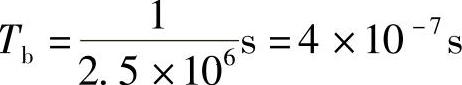 ,故Eb=A2Tb=4×10-15J。
,故Eb=A2Tb=4×10-15J。
(1)当传输单极性信号时,用式(5-11)求得单极性时的误码率为
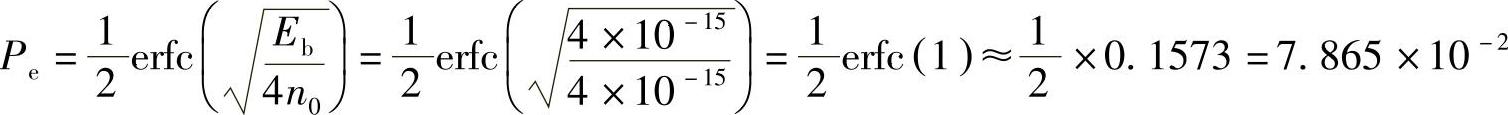
(2)当传输信号为双极性时,用式(5-11)求得双极性信号的误码率为
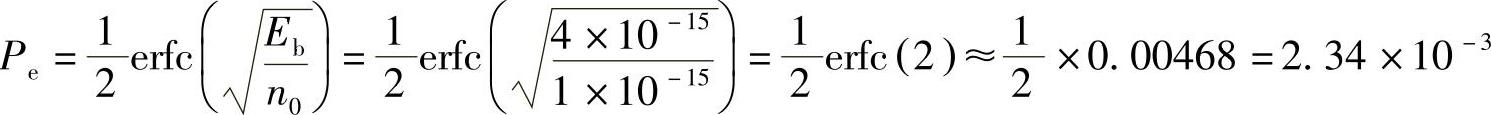
9.码元间隔为Tb的二进制随机序列110110001011…,码元“1”对应的波形为升余弦脉冲,持续时间为2Tb,码元“0”对应的波形与“1”码波形极性相反。
(1)当示波器扫描周期T0=Tb时,试画出眼图。
(2)当T0=2Tb时,试重画眼图。
解:首先画出要在示波器上显示的波形,如图5-20所示。

图5-20 波形合成过程
(1)在图5-20上,从1.5Tb时刻开始,截取T0=Tb长度的波形段,将各段波形叠加在一起,得到如图5-21所示的眼图(图形有所放大)。
(2)在图5-20上,从1.5Tb时刻开始,截取T0=2Tb长度的波形段,将各段波形叠加在一起,得到如图5-22所示的眼图。
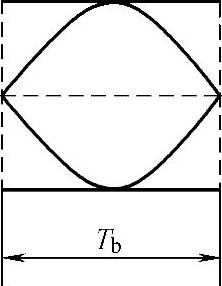
图5-21 T0=Tb长度波形段叠加后的眼图
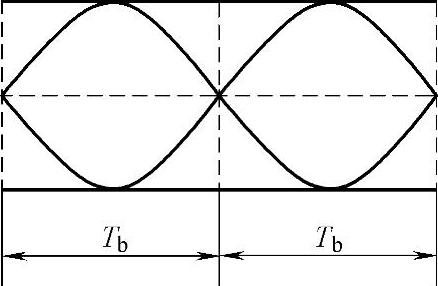
图5-22 T0=2Tb长度波形段叠加后的眼图
说明:本题在求解过程中,必须首先画出合成波形,因为码元波形宽度为2Tb,而码元间隔为Tb,所以波形间有重叠。在画眼图时,波形需要截段,应注意截取的开始时刻,否则不能形成清晰的眼图。
10.有一个三抽头时域均衡器如图5-21所示。若输入信号x(t)的取样值为x-2=1/8,x-1=1/3,x0=1,x+1=1/4,x+2=1/16,其余取样值均为0。求均衡器输入及输出波形的峰值失真。
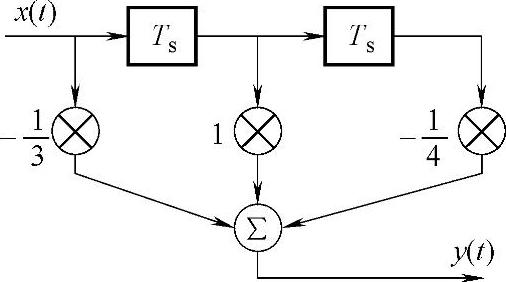
图5-23 三抽头时域均衡器
解:由图5-23可知,均衡器抽头系数为c-1=-1/3,c0=1,c1=-1/4,由式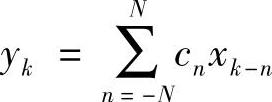 可计算出y(t)在各取样时刻的值为
可计算出y(t)在各取样时刻的值为
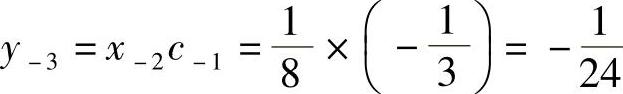
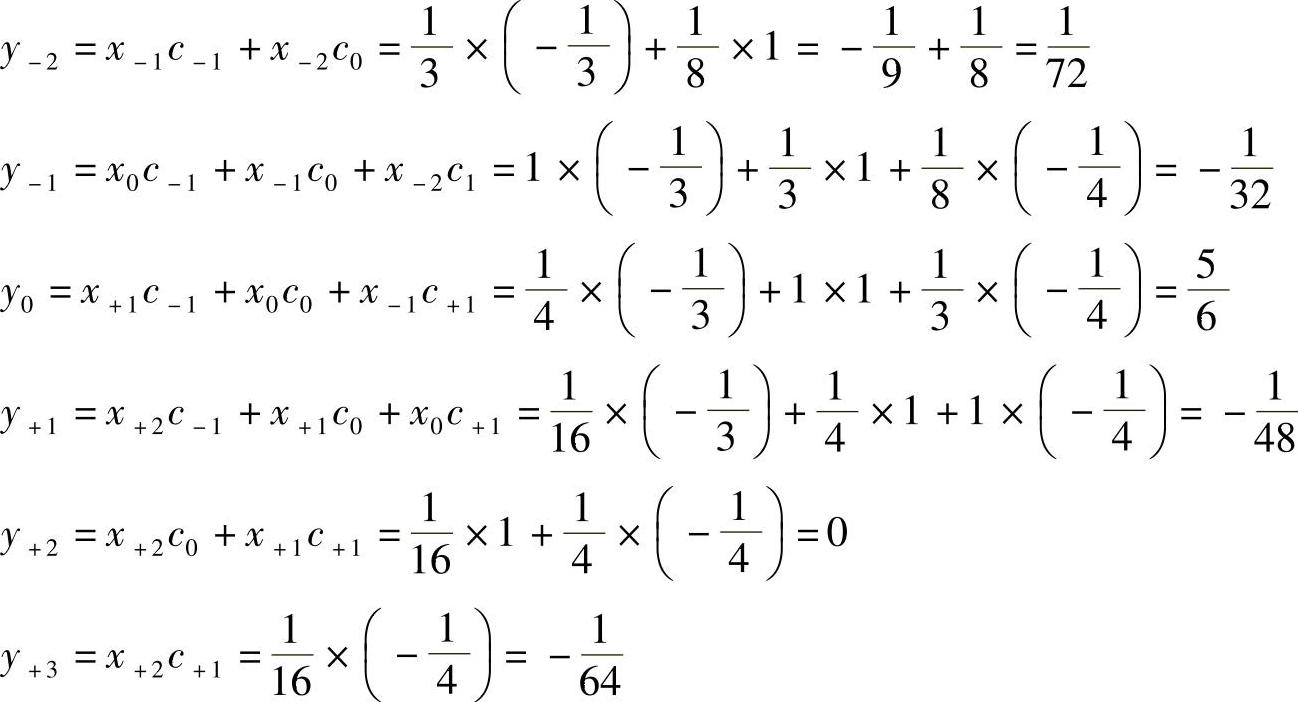
其余yk的值为0。
由式(5-15)和式(5-14)可计算出均衡前后的峰值畸变失真分别为
均衡器输入峰值畸变失真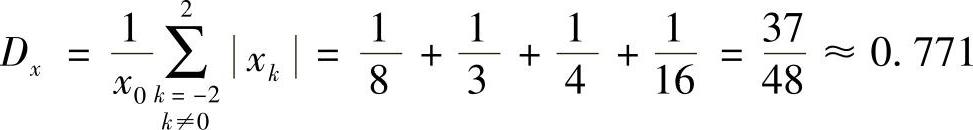
均衡器输出峰值畸变失真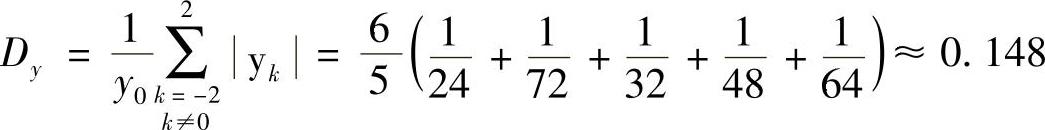
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




