1.有扰连续信道的信道容量为104bit/s,信道带宽为3kHz。如果将信道带宽提高到10kHz,在保持信道容量不变的情况下,信号噪声功率比可降到多少?
解:若C=104bit/s且B=3kHz=3000Hz,则所需的信噪比为
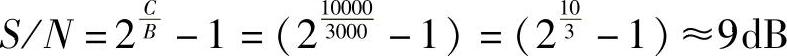
若保持C=104bit/s,将信道带宽提高到B=10kHz=10000Hz,则所需的信噪比为
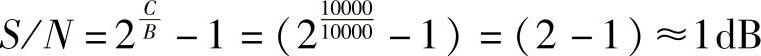
可见,在保持信道容量不变时,提高信道带宽可换取对信噪比要求的降低。这种信噪比和带宽的互换在通信工程中有很大的用处。例如,在宇宙飞船与地面的通信中,飞船上的发射机功率不可能很大,因此可用增大带宽的方法来换取对信噪比要求的降低。相反,如果信道频带比较紧张,如有线载波电话信道,这时主要考虑频带利用率,可提高信号功率来提高信噪比,从而降低对信道带宽的要求。
2.设数字信号每比特信号能量为Eb,信道噪声的双边功率谱密度为n0/2。试证明:信道无差错传输的最小Eb/n0为-1.6dB。
证明:信号功率为S=EbRb,噪声功率为N=n0B,令C=Rb,得到
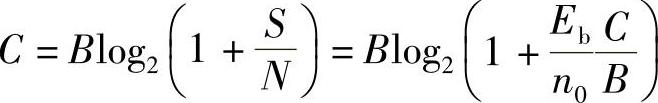
对上式做适当变换得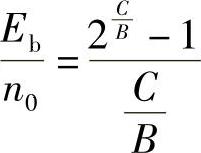 ,当
,当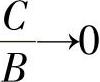 时,得
时,得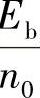 的最小值为
的最小值为
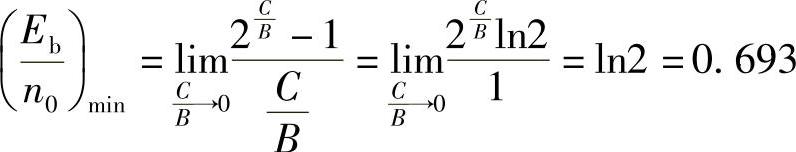
用分贝来表示,得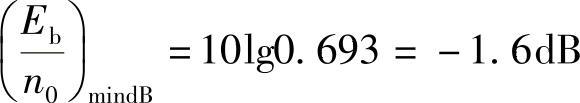
3.信号s1(t)=2cos8πt+2cos16πt和信号s2(t)=2cos30πt+2cos35πt分别通过图3-11所示的恒参信道。
(1)指出它们存在何种失真?
(2)写出输出表达式。
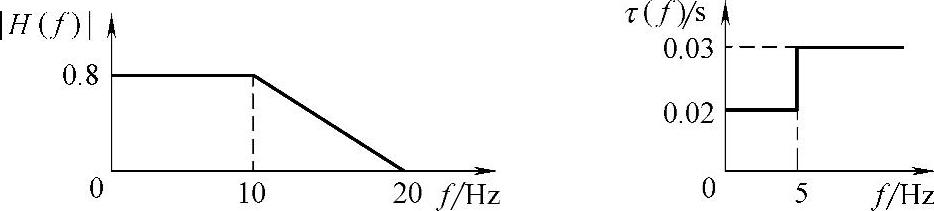
图3-11 某信道幅频特性和群时延特性
解:(1)信号s1(t)含有两个频率成分,频率分别为4Hz和8Hz。由图3-11所示的幅频特性可知,这两个频率成分通过时,均受到信道的衰减,且衰减幅度相同,均为0.8,故s1(t)通过此信道时不会引起幅频失真。由信道的群时延特性可见,4Hz频率成分通过时受到的时间时延为0.02s,而8Hz频率成分通过时则会受到0.03s的时间时延,可见有群时延失真,即有相频失真。同理,s2(t)的两个频率成分分别是15Hz和17.5Hz,通过图3-11所示的信道时,受到的幅度衰减分别为0.4和0.2,受到的时间时延均为0.03s,故s2(t)通过此信道时存在幅频失真,但不会引起群时延(相频)失真。
(2)综合上述分析,s1(t)=2cos8πt+2cos16πt通过信道后的输出表达式为
s1o(t)=2×0.8cos8π(t-0.02)+2×0.8cos16π(t-0.03)(https://www.xing528.com)
s2(t)=2cos30πt+2cos35πt通过信道后的输出表达式为
s2o(t)=2×0.4cos30π(t-0.03)+2×0.2cos35π(t-0.03)
4.有多径传播信道模型如图3-12所示,设t0和τd均为常数。求
(1)当输入信号为s(t)时的输出信号r(t)。
(2)对该信道的传输特性加以讨论。
(3)信号通过此信道有失真吗?
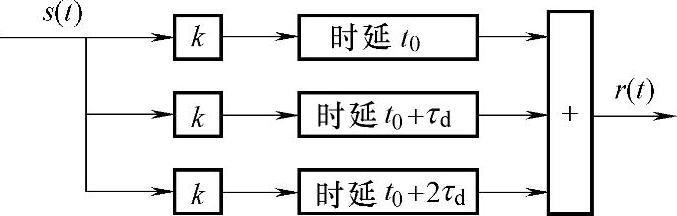
图3-12 三径传播信道模型
解:(1)根据信道模型直接写出输出信号表达式
r(t)=ks(t-t0)+ks(t-t0-τd)+ks(t-t0-2τd)
(2)方法一:直接写出冲激响应,再求傅里叶变换得信道传输特性。
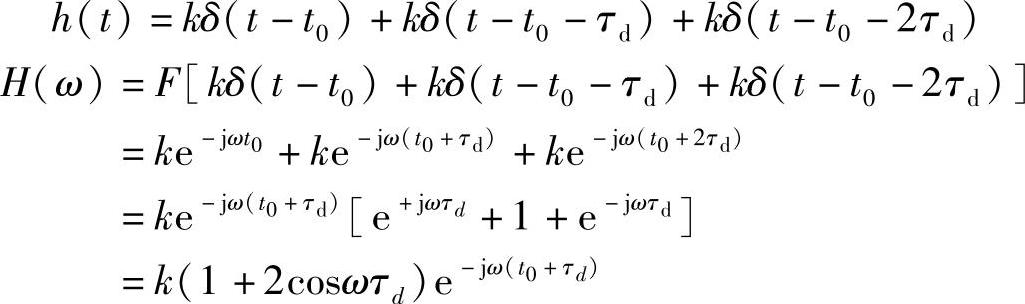
方法二:对输出信号表达式两边求傅里叶变换,再根据系统传输特性的定义求得。
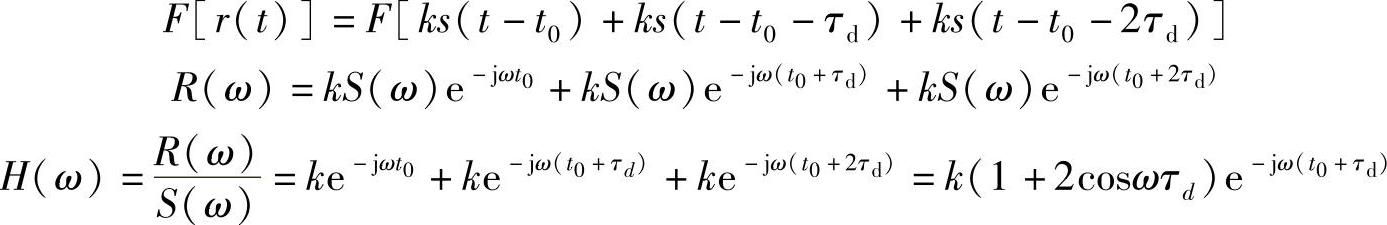
讨论:
1)其幅频特性|H(ω)|=k|1+2cosωτd|,其相频特性ϕ(ω)=ω(t0+τd),群时延特性为τ(ω)=t0+τd。
2)幅频特性不是一条水平线,故有幅频失真。相频特性是ω的线性函数,群时延特性是一水平线,此信道无相频失真。
(3)单频信号通过此信道无失真,非单频信号通过有失真,因为此信道有幅频失真。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




