教材习题详解：取样函数在通信原理中的应用

1.已知x（t）为图2-10所示的宽度为2ms的矩形脉冲。

（1）写出x（t）的傅里叶变换表达式。

（2）画出它的频谱函数图。

解：（1）利用矩形脉冲频谱函数的表达式，并将脉冲宽度τ=0.002s和脉冲幅度A=1V代入即可得到结果为

X（f）=AτSa（πfτ）=0.002Sa（0.002πf）

注意：应将时间单位换算成秒，这样频率的单位就为赫兹。

（2）频谱函数如图2-11所示。

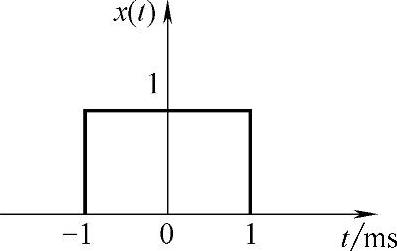
图2-10 矩形脉冲

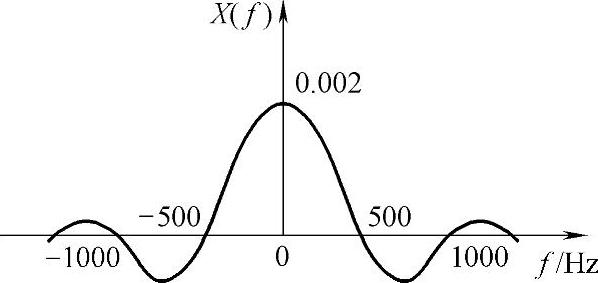
图2-11 频谱函数

画此频谱图时抓住三点即可：①取样函数的形状；②最大幅度为Aτ，即为矩形的面积；③正频率方向第一个零点为1/τ，即矩形脉冲宽度的倒数，其他零点依次为2/τ，3/τ，…，负频率方向的零点位置与它们对称。

取样函数在通信原理的学习中经常用到，其形状、最大幅度值及频率轴上的零点分布应熟记。

2.x（t）为如图2-12所示的周期函数，已知τ=2ms，T=8ms。

（1）写出x（t）的指数型傅里叶级数展开式。

（2）画出振幅频谱图。

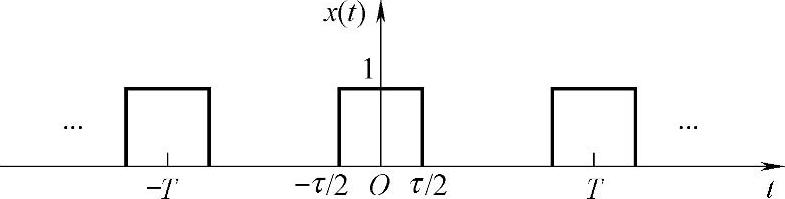
图2-12 周期函数

解：（1）指数型傅里叶级数展开式表示为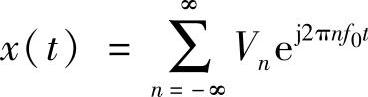，故需要求出V_n。对于矩形周期脉冲信号，由式（2-4）可知

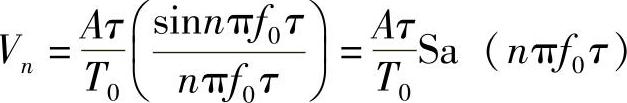
将本题中的参数T₀=8ms=0.008s、τ=2ms=0.002s、A=1V代入上式得

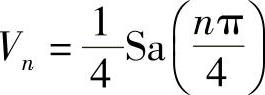
于是有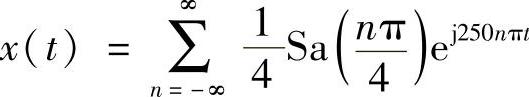

（2）振幅谱|V_n|～f如图2-13所示。

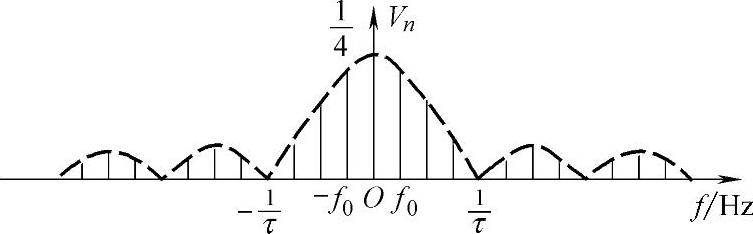
图2-13 振幅频谱图

图中，。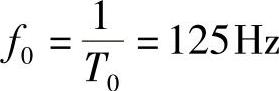

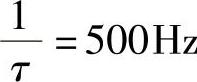由图2-13可见，振幅谱的包络（虚线）与矩形脉冲的频谱函数曲线形状相同，只是负值部分向上翻了，离散谱线位于nf₀处。因此，画此图时可分两步：先根据矩形脉冲的有关参数画出振幅谱的包络；再根据周期计算出f₀=1/T₀，然后在nf₀处画离散谱线，谱线高度与该位置的包络值相同。

3.已知x（t）的频谱函数如图2-14所示，设f₀=5f_x，画出x（t）cos2πf₀t的频谱函数图。

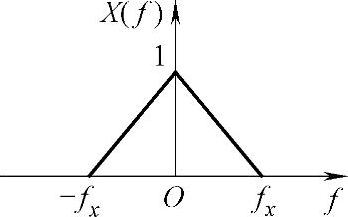
图2-14 频谱函数

解：首先求出x（t）cos2πf₀t的频谱函数。

方法1：利用欧拉公式和频移特性求解。

根据欧拉公式得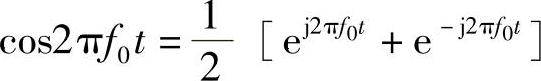

于是有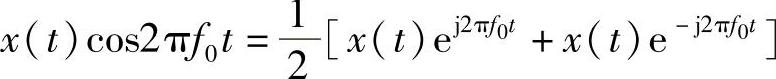

再利用频移特性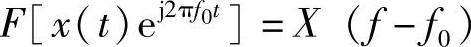得到

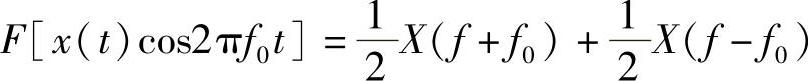
方法2：利用卷积特性来求，即

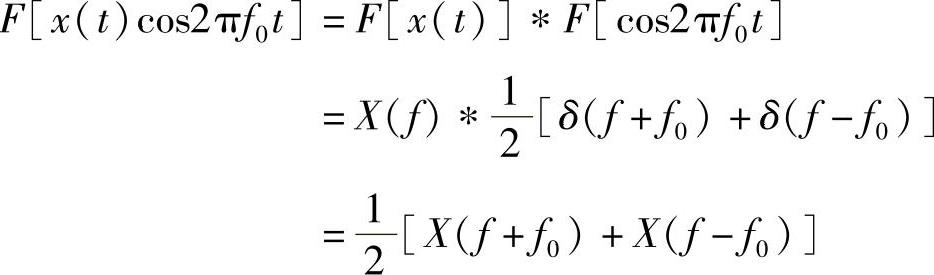
方法3：利用调制特性直接写出，即

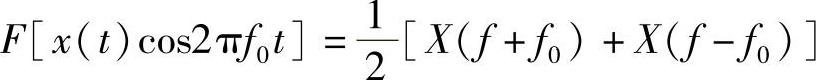
这种方法最直接，且在后面的调制部分学习中会反复用到，应熟记。

根据上述求得的频谱函数及f₀=5f_x画出频谱图如图2-15所示。

4.已知x（t）的波形如图2-16所示。

（1）如果x（t）为电压并加到1Ω电阻上，求消耗的能量为多大？

（2）求x（t）的能量谱密度G（f）。

（3）求x（t）的卷积x（t）∗x（t）。

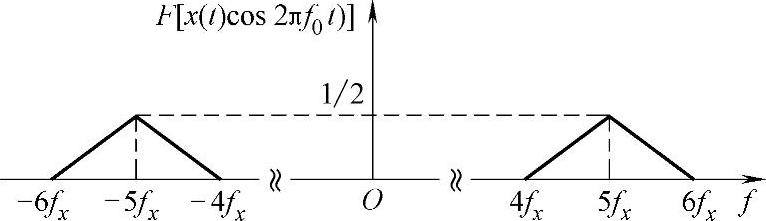
图2-15 频谱图

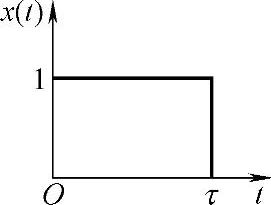
图2-16 波形示意图

解：（1）在时域中，对1Ω电阻上的瞬时功率求积分，即

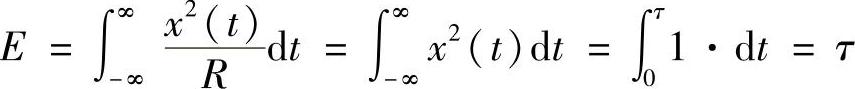
（2）由能量谱的定义G（f）=|X（f）|²可知，要求能量谱，需先求出x（t）的频谱。x（t）是由中心在原点、幅度为1V、宽度为τ的矩形脉冲时延τ/2得到的信号。根据本题给出的有关参数，中心在原点的矩形脉冲的频谱为

D（f）=τSa（πfτ）

利用时延特性可得时延τ/2后信号的频谱为

X（f）=τSa（πfτ）·e^-j2πfτ/2=τSa（πfτ）·e^-jπfτ

由此得到信号的能量谱密度为

G（f）=τ²Sa²（πfτ）

注意：能量谱只与信号的振幅谱有关，而与相位谱无关。由于时延只影响信号的相位谱，因此时延对信号的能量谱不产生作用。

（3）可以用卷积直接求，也可以先求出卷积结果的频谱，然后再求其傅里叶反变换。

方法1：用卷积直接求

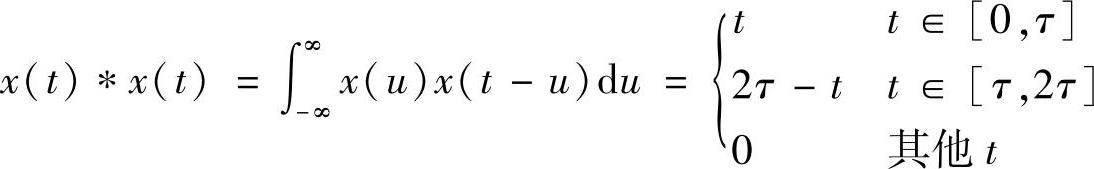
方法2：由（2）中已经求出的频谱X（f）和卷积特性得

F[x（t）∗x（t）]=X（f）·X（f）=τ²Sa²（πfτ）·e^-j2πfτ此频谱由τ²Sa²（πfτ）和e^-j2πfτ组成，前者的傅里叶反变换为三角波形，可从常用时间函数及其傅里叶变换表中查得，仔细对比表达式，可确定τ²Sa²（πfτ）频谱所对应的三角波的幅度为τ、宽度为2τ。根据时延特性，频谱上乘以e^-j2πfτ等效为时间上时延τ。故同样可得

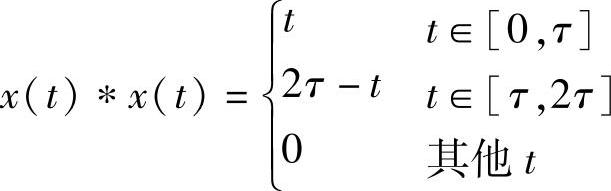
此问题的目的是检查傅里叶变换的卷积特性，故希望读者采用方法2来完成。

5.已知功率信号x（t）=Acos（200πt）sin（2000πt），试求

（1）该信号的平均功率。

（2）该信号的功率谱密度。

（3）该信号的自相关函数。

解：（1）利用三角公式2sinAcosB=sin（A-B）+sin（A+B）将x（t）转换成两个正弦之和，即

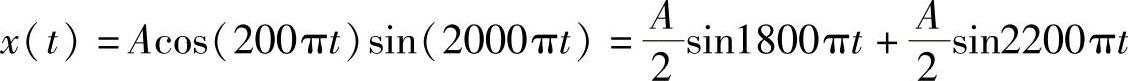
其功率等于两个正弦信号的功率之和，故x（t）的功率（平均功率）为

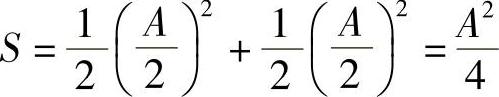
（2）用欧拉公式将周期信号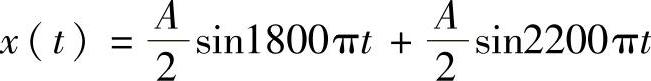表示成指数型级数形式，即

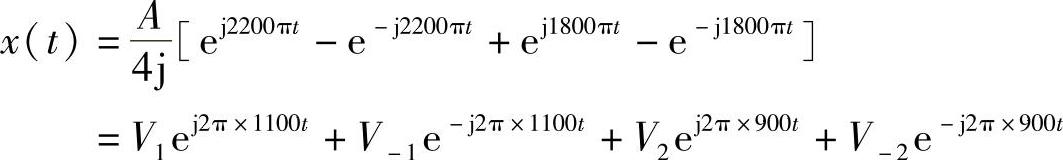
式中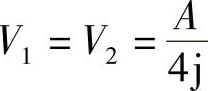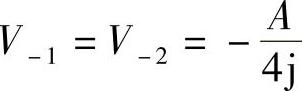，、，用公式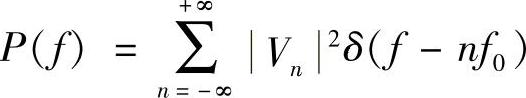得功率谱为

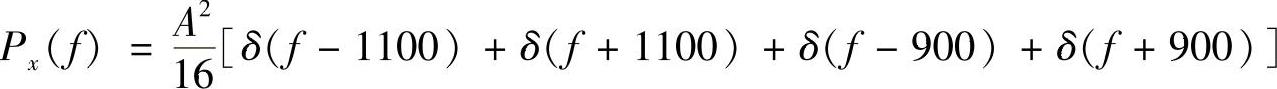
功率谱密度示意图如图2-17所示。

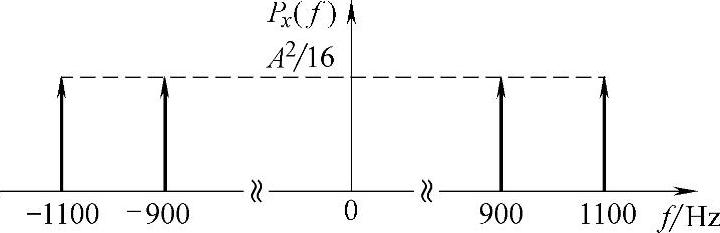
图2-17 功率谱密度

（3）周期信号的功率谱密度与其自相关函数是一对傅里叶变换，故其自相关函数为

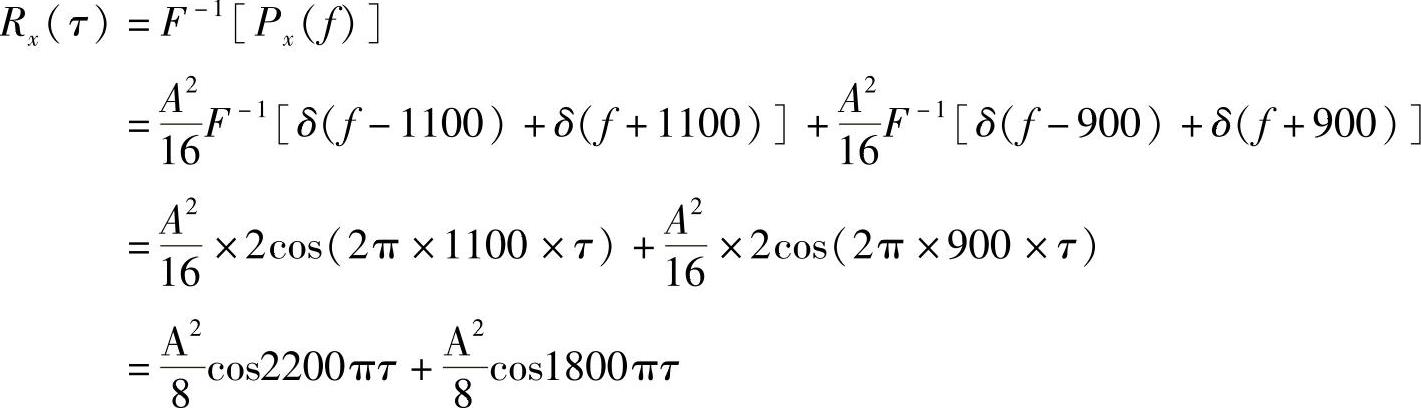
此题涉及的知识点有：三角公式；欧拉公式；周期信号的指数表示；周期信号的功率谱密度表示式；功率谱密度与自相关函数是一对傅里叶变换；余弦信号的傅里叶变换。

6.已知x（t）如图2-18所示。

（1）求X（f）。（提示：可查书中常用函数的傅里叶变换表）

（2）当τ增加时，此信号的能量是增加还是减小？

（3）若此信号通过图2-14所示的低通滤波器，则随着τ的增加，滤波器输出端的能量是增加还是减小？

解：（1）由常用函数的傅里叶变换表查得，三角脉冲的频谱为

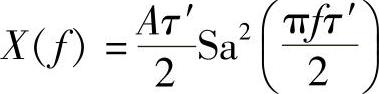
式中，A为三角脉冲的振幅；τ′为三角脉冲的宽度。将本题中的A=1V、τ′=2τ代入上式得

X（f）=τSa²（πfτ）

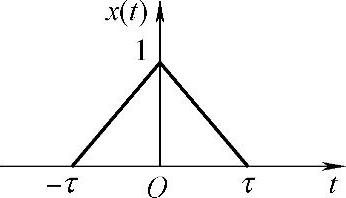
图2-18 波形示意图

（2）在时域求信号能量的公式为

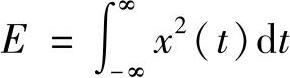
图2-18所示三角脉冲的数学表达式为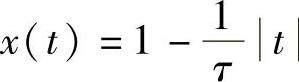，t≤τ，代入能量公式得此信号的能量为

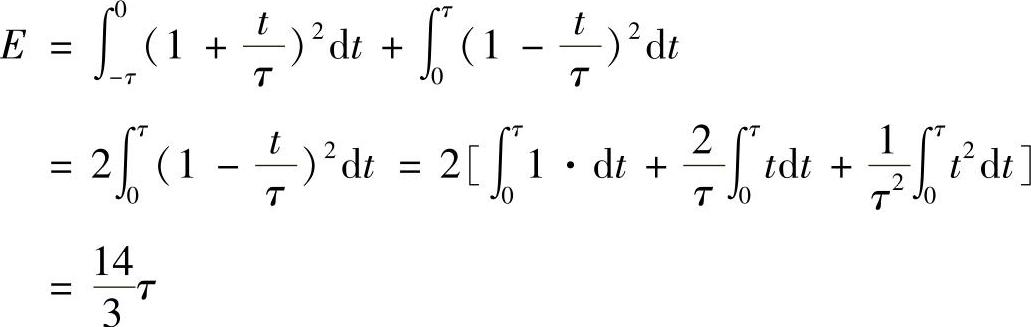
可见，随着τ的增加，此信号的能量会增大。

（3）增加。可以从两个方面来说明：

1）随着τ的增大，信号的能量变大。

2）随着τ的增大，三角脉冲的频谱越来越集中到零频附近（时域无限，频域有限），因此通过图2-14所示的低通滤波器的部分占整个信号的比例就越高。例如，当τ→∞时，信号的频谱变成冲激脉冲，此冲激频谱能量全部通过低通滤波器，此时滤波器输出信号的全部能量。

7.已知某信号的频谱函数为Sa²（πfτ），求该信号的能量。（提示：先通过计算及查表得到其时域波形，然后在时域求其能量）

解：根据帕塞瓦尔定理，信号的能量既可以在频域求，也可以在时域求，即

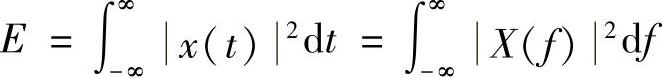
由于已知信号的频谱函数为X（f）=Sa²（πfτ），可见在频域求此信号的能量很难计算积分。故应考虑用时域积分来求解。

此信号对应的时域信号为三角脉冲，查常用信号的傅里叶变换表得，幅度为A′、宽度为τ′的三角脉冲的频谱函数为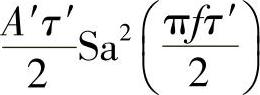，将此表达式与已知表达式对比，确定已知信号是幅度为1/2、宽度为2τ的三角脉冲，其数字表达式为

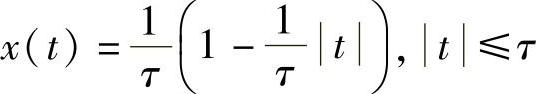
参考题6的解法，求得给定信号的能量为

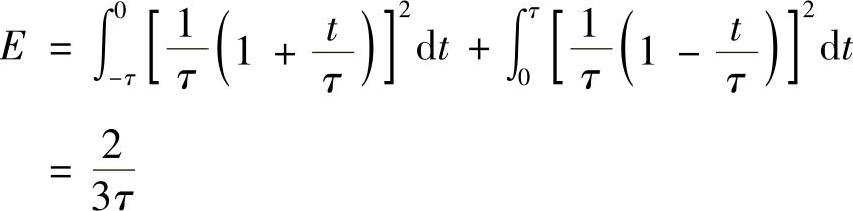
8.试计算电压v（t）=Sa（2πFt）在100Ω电阻上消耗的总能量。（提示：先求出其能量谱密度）

解：在时域是取样函数的信号，其频谱是矩形。因此在频域求此信号的能量会更方便。

根据常用傅里叶变换得，幅度为A、宽度为B的矩形频谱的傅里叶反变换（时域信号）为x（t）=ABSa（πBt），将此与v（t）=Sa（2πFt）对比，即

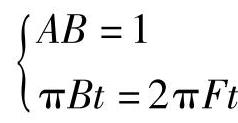得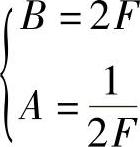

确定v（t）的频谱V（f）是个幅度为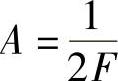、宽度为B=2F的矩形。

故电压v（t）在100Ω电阻上消耗的总量为

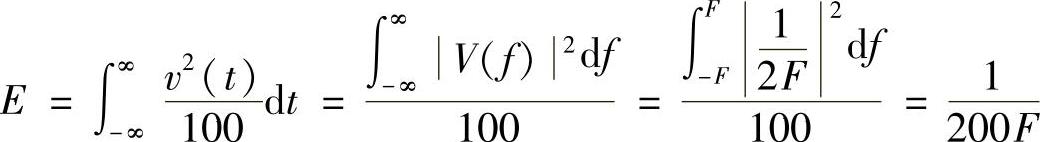
9.如图2-19所示，冲激脉冲δ（t）通过一个线性网络后，再经过相乘器输出为g₂（t）。

若线性网络的传输特性为H（f）=τSa²（πfτ），试求

（1）网络输出响应g₁（t）的表示式。

（2）相乘器输出响应g₂（t）的表达式及其频谱函数G₂（f）。

（3）画出g₁（t）、g₂（t）的波形和它们的频谱函数图（假设f_c>>1/τ）。

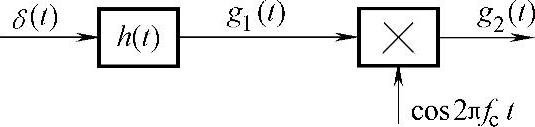
图 2-19

解：（1）输入为冲激信号，故网络输出响应g₁（t）就是网络的冲激响应。根据网络传输特性表达式可知，其冲激响应是幅度为1V、宽度为2τ的三角波，即

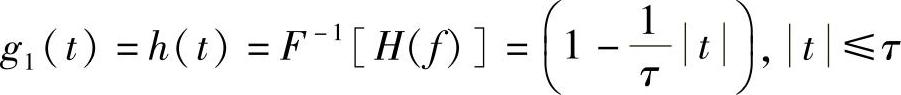
其频谱等于网络传输特性，即

G₁（f）=H（f）=τSa²（πfτ）

（2）相乘器输出响应g₂（t）的表达式为

g₂（t）=g₁（t）cos（2πf_ct）

由调制特性得频谱函数为

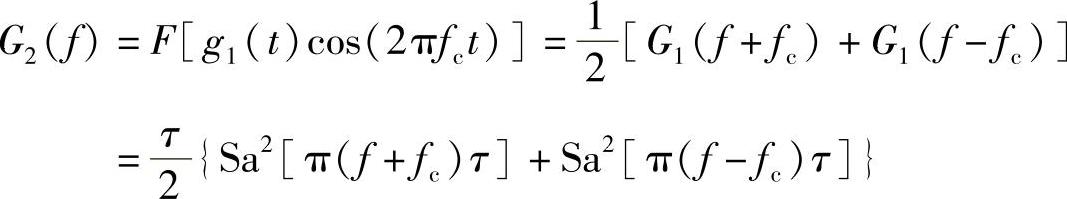
（3）当f_c>>1/τ时，g₁（t）、g₂（t）的波形及它们的频谱示意图如图2-20所示。

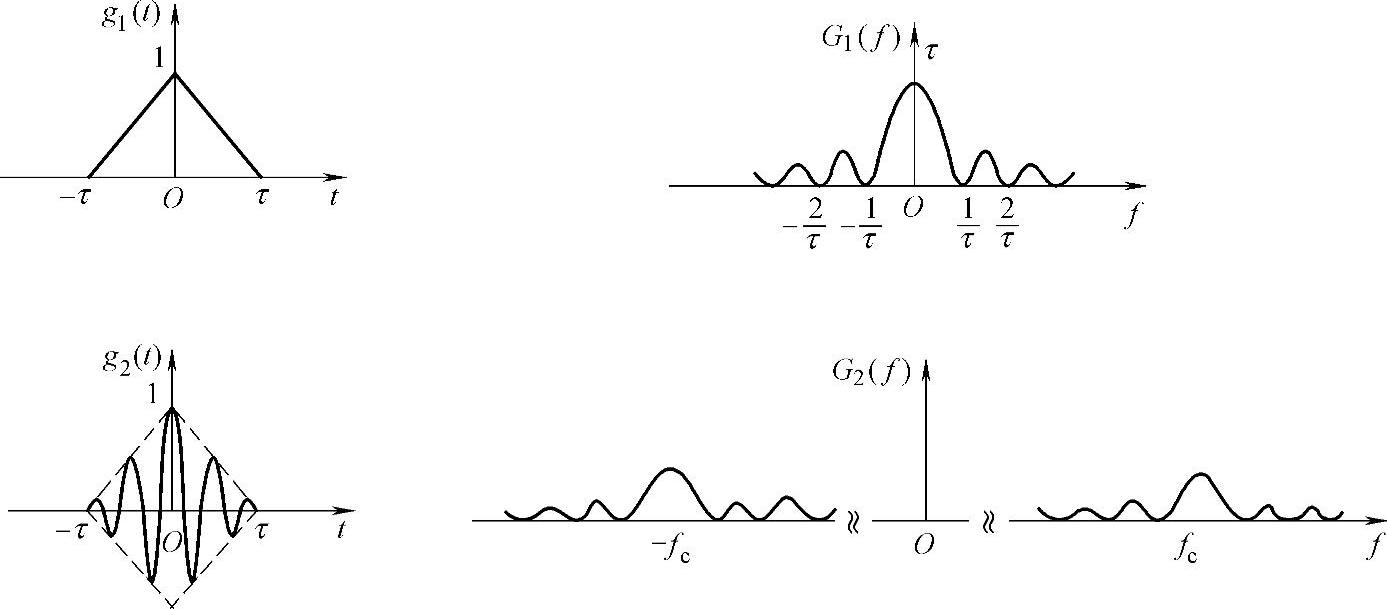
图2-20 波形及频谱示意图

10.随机变量X具有如下的均匀概率密度函数，求其数学期望和方差。

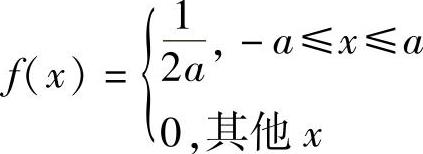
解：此随机变量为连续随机变量，应用相应公式求得其数学期望和方差分别为

数学期望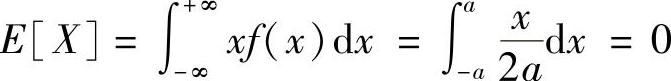

方差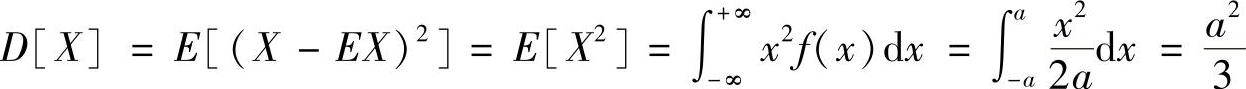此题的目的是训练连续随机变量的数学期望和方差的求解。

11.随机变量X具有如下的瑞利概率密度函数，求其数学期望和方差。

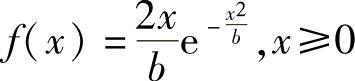
解：（1）数学期望E[X]为

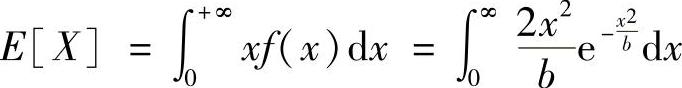
令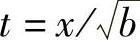，则

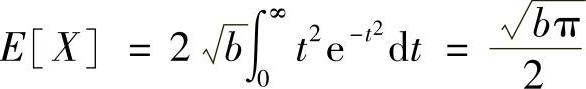
查积分表得。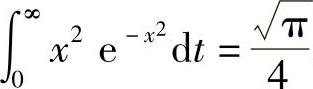

（2）方差D[X]为

D[X]=E{[X-E（X）]²}=E[X²]-[E（X）]²其中

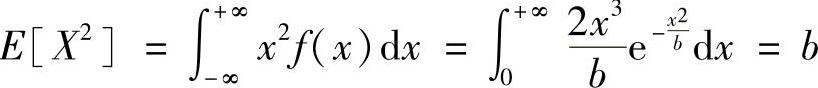
得方差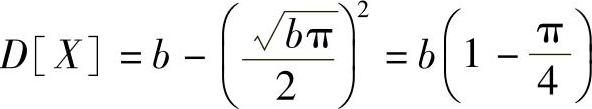

12.具有上题所示的瑞利概率密度函数的随机变量，已知方差是7，则其均值是多少？随机变量大于均值且小于10的概率是多少？

解：（1）由D[X]=b（1-π/4）=7，可求得b=32.618，代入均值表达式得

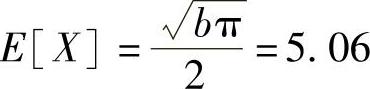
（2）对概率密度函数求积分等于求概率，故随机变量大于均值5.06且小于10的概率为

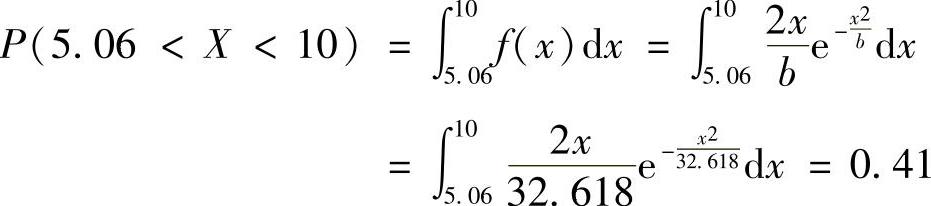
13.设随机变量X、Y和随机变量θ之间的关系为：X=cosθ，Y=sinθ，并设θ在0～2π的范围内均匀分布，试说明X和Y是不相关的，且不是统计独立的。

解：（1）要说明X和Y不相关，需证明其协方差Cov（X，Y）=0。根据定义

Cov（X，Y）=E[（X-a_X）（Y-a_Y）]

已知f（θ）=1/2π，可得

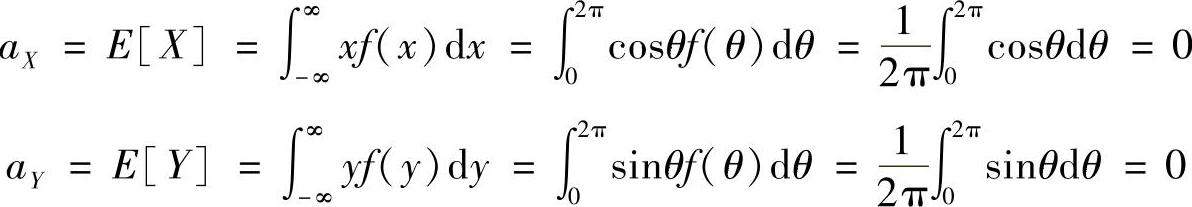(www.xing528.com)

因此有

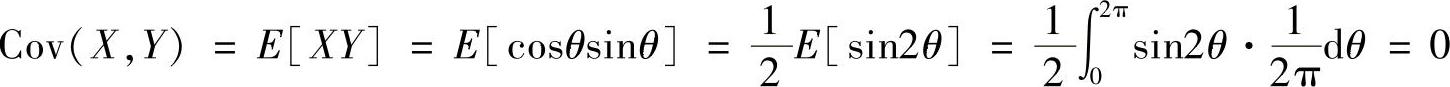
（2）要说明X和Y不是统计独立的，只要证明存在a，b有P（X≤a，Y≤b）≠P（X≤a）·P（Y≤b）即可。

设a=b=1/2，则有

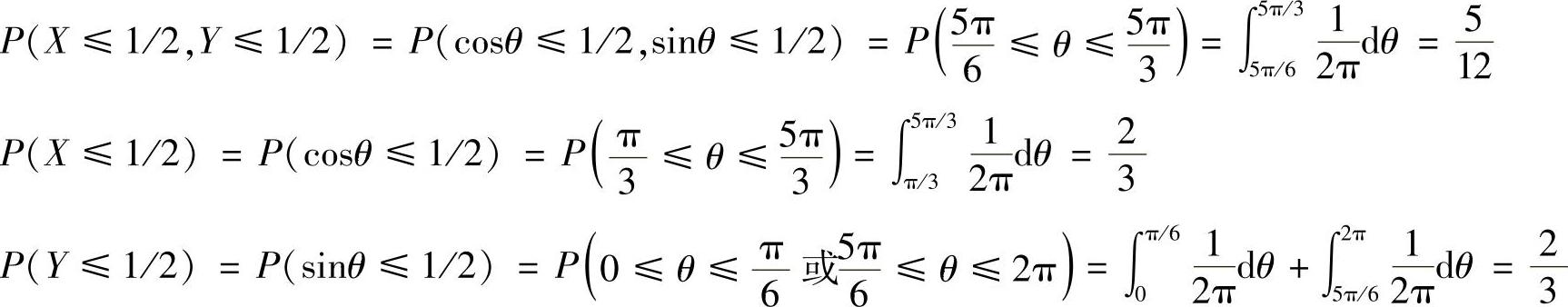
可见，P（X≤1/2，Y≤1/2）≠P（X≤1/2）P（Y≤1/2），所以X和Y不是统计独立的。

14.两个随机过程X（t）、Y（t）的样本函数如图2-21所示，假设各样本函数等概出现。

（1）求X（t）的数学期望a_X（t）和自相关函数R_X（t，t+τ）。问X（t）平稳吗？

（2）求Y（t）的数学期望a_Y（t）和自相关函数R_Y（t，t+τ）。问Y（t）平稳吗？

解：（1）对于随机过程X（t），有

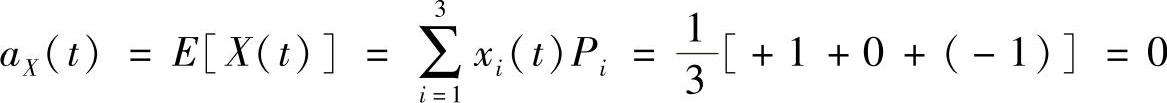
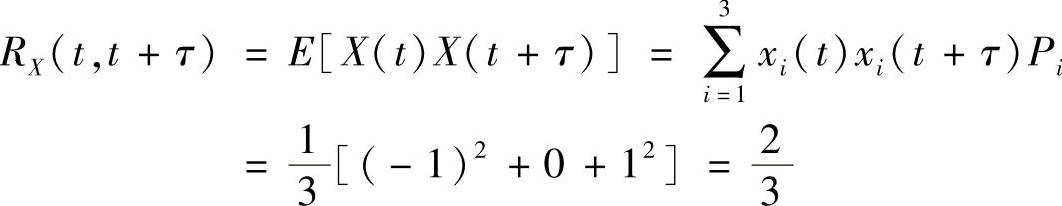
由于均值a_X（t）是常数，自相关函数R_X（t，t+τ）与时间t无关，故随机过程X（t）是广义平稳的。

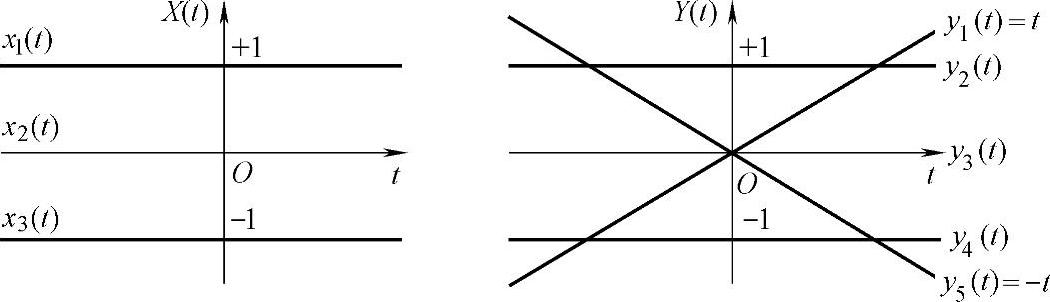
图2-21 随机过程的样本函数

（2）对于随机过程Y（t），有

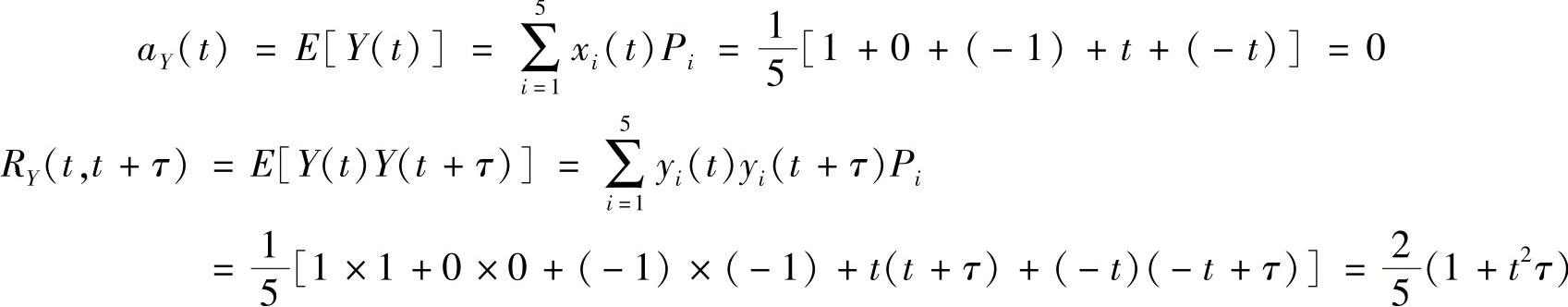
由于自相关函数R_Y（t，t+τ）与时间t有关，故随机过程Y（t）不是广义平稳的。

15.设有两个随机过程S₁（t）=X（t）cos2πf₀t，S₂（t）=X（t）cos（2πf₀t+θ），X（t）是广义平稳过程，θ是对X（t）独立的、均匀分布于（-π，π）上的随机变量。求S₁（t）、S₂（t）的自相关函数，并说明它们的平稳性。

解：已知X（t）是平稳随机过程，则其均值为常数，自相关函数只与时间间隔有关，分别设E[X（t）]=a_X，R_X（t，t+τ）=R_X（τ）。又知θ是独立于X（t），且。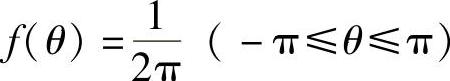

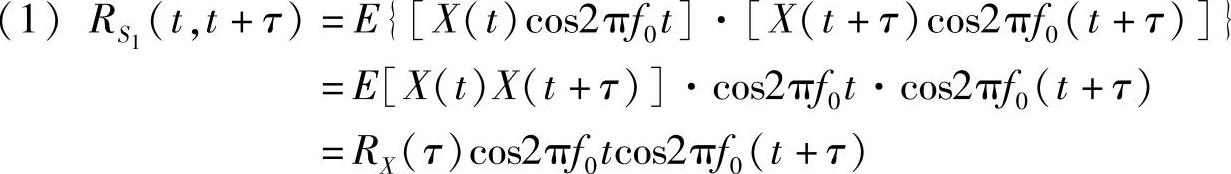
随机过程S₁（t）的自相关函数与时间t有关，故不是平稳随机过程。

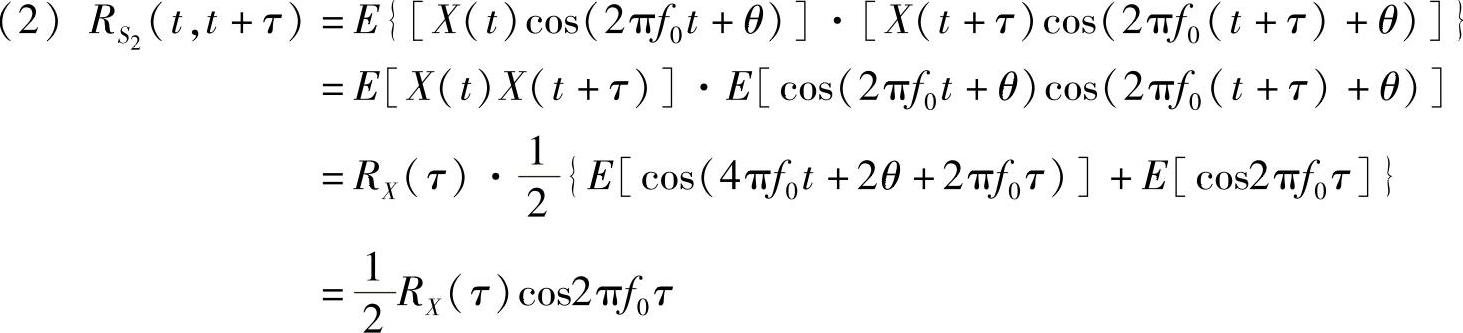
其中，。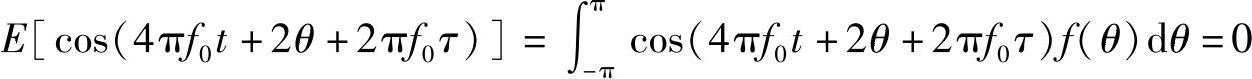

随机过程S₂（t）的均值为

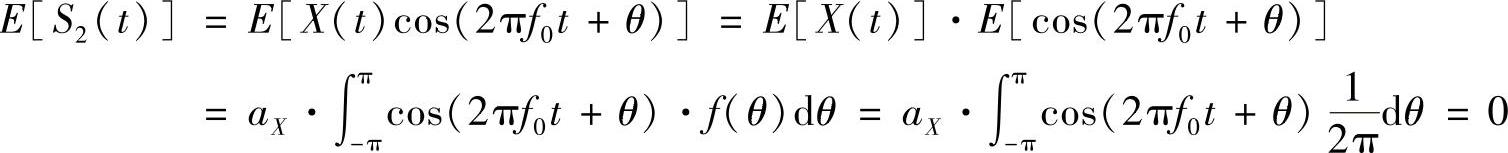
可见，S₂（t）的均值为常数，自相关函数与t无关，所以是广义平稳随机过程。

16.考虑随机过程Z（t）=Xcos2πf₀t-Ysin2πf₀t，其中X，Y是独立的高斯随机变量，二者均值为0，方差是σ²。试说明Z（t）也是高斯的，且均值为0，方差为σ²，自相关函数R_Z（τ）=σ²cos2πf₀τ。

解：（1）由于cos2πf₀t、sin2πf₀t任意时刻的值是确定的，因此Z（t）是高斯随机变量X、Y的线性组合，故也是高斯随机变量。

（2）Z（t）的均值为

a_Z（t）=E[Z（t）]=E[Xcos2πf₀t-Ysin2πf₀t]=cos2πf₀t·E[X]-sin2πf₀t·E[Y]=0

（3）Z（t）的方差可用下列两种方法中的任一种方法来求。

方法1：

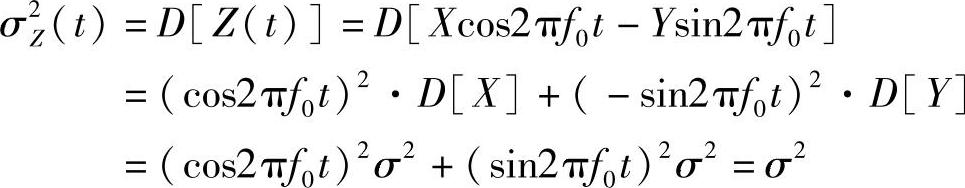
方法2：

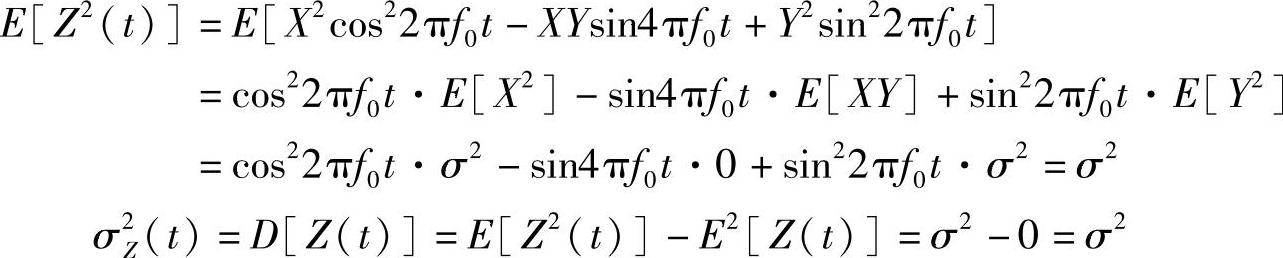
（4）Z（t）的自相关函数为

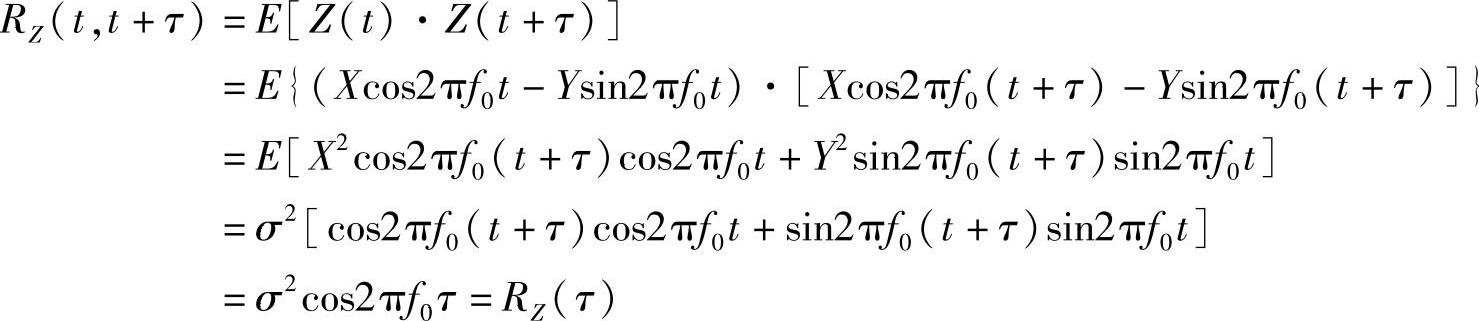
17.考虑随机过程Z（t）=X（t）cos2πf₀t-Y（t）sin2πf₀t，其中X（t）、Y（t）是高斯的、零均值、独立的随机过程，且有R_X（τ）=R_Y（τ）。

（1）试证R_Z（τ）=R_X（τ）cos2πf₀τ。

（2）设R_X（τ）=σ²e^-aτ（a＞0），求功率谱密度函数P_Z（f），并做图。

解：（1）由随机过程自相关函数的定义，得

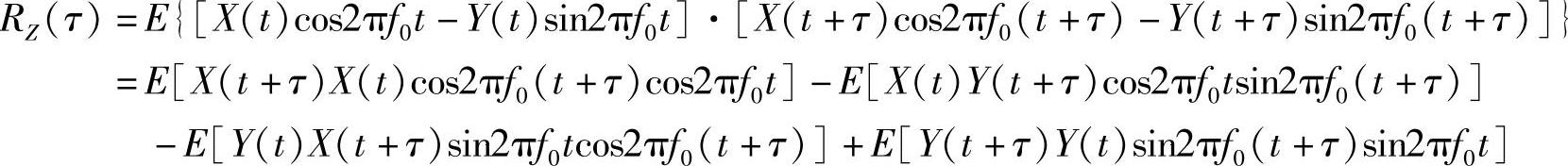
由于已知随机过程X（t）与Y（t）是独立的，且为零均值平稳过程，所以有

E[X（t）Y（t+τ）]=E[X（t）]·E[Y（t+τ）]=0

E[Y（t）X（t+τ）]=E[Y（t）]·E[X（t+τ）]=0

则上式为

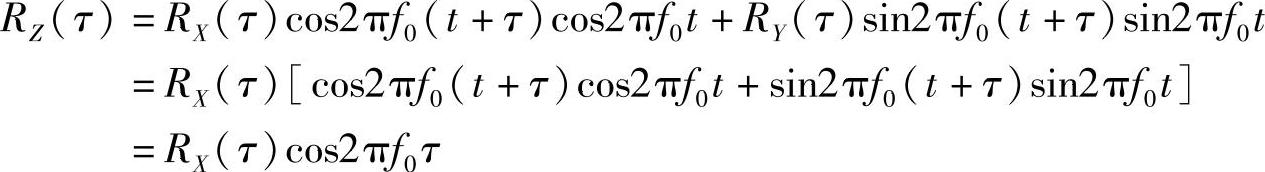
（2）P_Z（f）与R_Z（τ）=R_X（τ）cos2πf₀τ是一对傅里叶变换

查常用函数傅里叶变换表可得R_X（τ）=σ²e^-a|τ|（双边指数脉冲）的傅里叶变换为

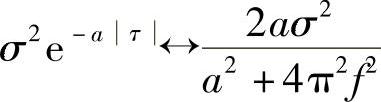
再利用调制特性即可得到

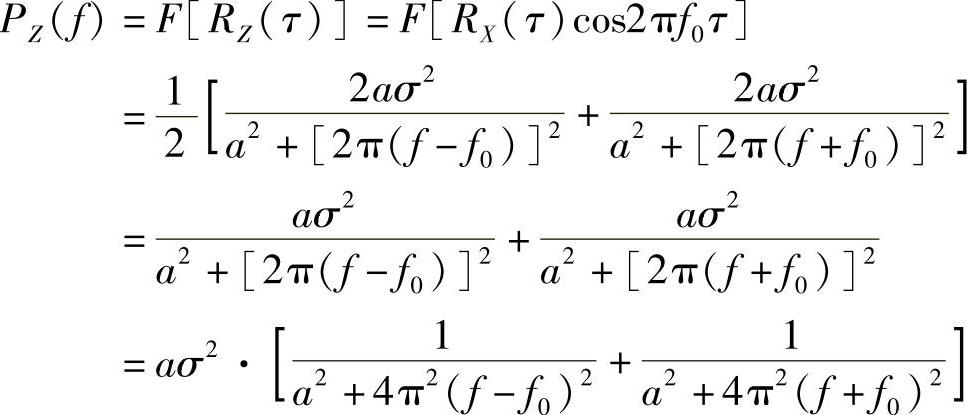
是频谱函数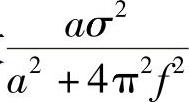分别在频率轴上的左右搬移，则f₀>>0时的示意图如图2-22所示。

18.一个均值为零的随机信号S（t），具有图2-23所示的三角形功率谱。问

（1）信号的平均功率S为多少？

（2）试证其自相关函数为R（τ）=S·Sa²（πBτ）。

（3）设B=1MHz，K=1（μV）2/Hz。试证信号的方均根值为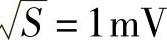，以及相距1μs的S（t）的两个取样值是不相关的。

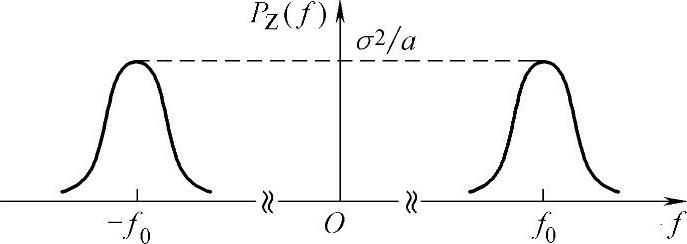
图2-22 f₀>>0时的示意图

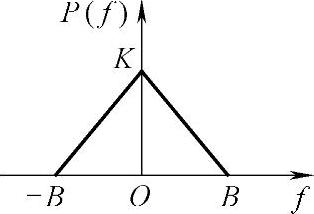
图2-23 三角形功率谱

解：（1）对功率谱积分即可得到信号的平均功率。故

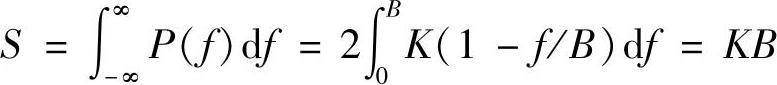
对P（f）积分的结果等于P（f）曲线下的面积，此处即为高为K、宽度为2B的三角形的面积，所以也可由三角形面积公式直接求得信号的平均功率。

（2）求随机信号的自相关函数通常有两种方法。一是利用定义R_S（t，t+τ）=E[S（t）S（t+τ）]，二是求功率谱的傅里叶反变换。此题可用方法二求得。

已知功率谱是个三角形频谱，查常用函数傅里叶变换表可知，高度为A、宽度为2f₀的三角形频谱X（f）其傅里叶反变换为

x（t）=Af₀Sa²（πf₀t）将本题参数（三角形频谱高K、宽度2B）代入，且将时间t换成τ即可得到自相关函数为

R（τ）=KBSa²（πBτ）=S·Sa²（πBτ）

（3）由S=KB=（1×10^-6V）²/Hz×1×10⁶Hz=10^-6V²得。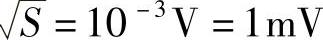

当τ=1μs时，R（τ）=S·Sa²（πBτ）=S·Sa²（π×10⁶×10^-6）=S·Sa²（π）=0，由于随机过程S（t）是零均值的，故C（τ）=R（τ）=0，可见，在随机过程S（t）上相距1μs的两个取值是不相关的。

19.零均值频带有限的白噪声n（t），具有功率谱P_n（f）=10^-6V²/Hz，其频率范围为-100kHz～100kHz。

（1）试证噪声的方均根值约为0.45V。

（2）求R_n（τ），且问n（t）和n（t+τ）在什么间距上不相关？

（3）设n（t）是服从高斯分布的，试求在任一时刻t，n（t）超过0.45V的概率是多少？超过0.9V的概率是多少？

解：（1）功率谱为P_n（f）=10^-6V²/Hz、频率范围为-100～100kHz的噪声其平均功率为

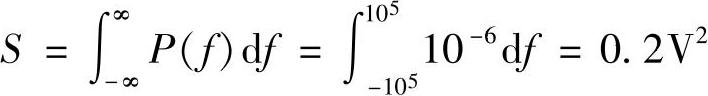
所以，噪声的方均根值。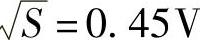

（2）自相关函数R_n（τ）与功率谱密度是一对傅里叶变换。已知噪声的功率谱是个矩形谱，由常用信号傅里叶变换可知，幅度为A、宽度为2f₀的矩形频谱其傅里叶反变换为

x（t）=2Af₀Sa（π·2f₀t）

由已知条件：噪声功率谱幅度为P_n（f）=10^-6V²/Hz、频度范围为-100～100kHz可知，A=10^-6，f₀=10⁵，代入上式且将时间t换成τ，得到噪声自相关函数为

R_n（τ）=0.2Sa（π×2×10⁵τ）

由于噪声均值为0，因此C_n（τ）=R_n（τ）=0.2Sa（π×2×10⁵τ）。

当C_n（τ）=0时，n（t）和n（t+τ）不相关。要使0.2Sa（π×2×10⁵τ）=0，需满足2π×10⁵τ=kπ，（k=±1，±2，…），解得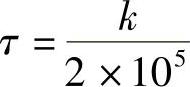。故当间距τ=5，10，15，…μs时两取样值不相关。

（3）已知n（t）是高斯随机过程，故其任意时刻的取值是个高斯随机变量，且均值为0，方差为σ²_n=S-E²[n（t）]=S-0=0.2V²。因此n（t）瞬时值的概率密度函数为

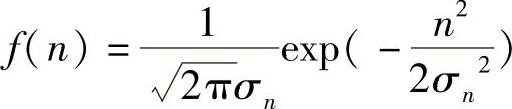
示意图如图2-24所示。则有

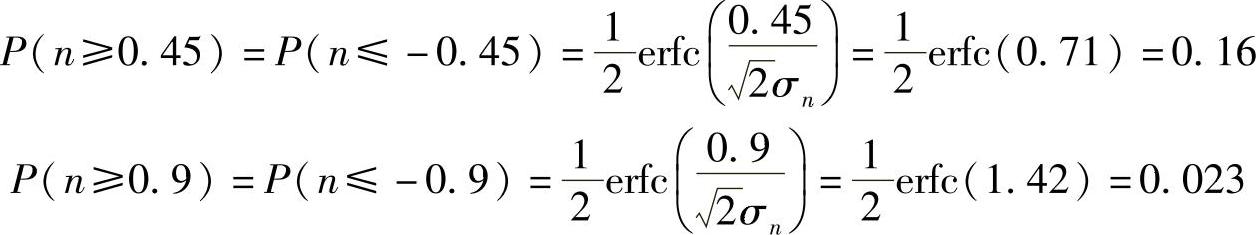
20.设输入随机过程X（t）是平稳的，功率谱为P_X（f），加于图2-25所示的系统。试证明输出过程Y（t）的功率谱为P_Y（f）=2P_X（f）（1+cos2πfT）。

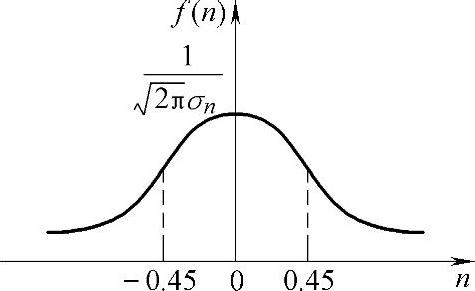
图2-24 高斯分布概率密度

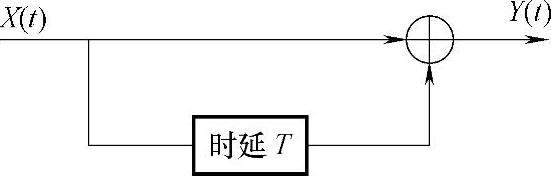
图 2-25

解：方法一：根据给定的系统组成，输出随机过程Y（t）=X（t）+X（t-T），则自相关函数为

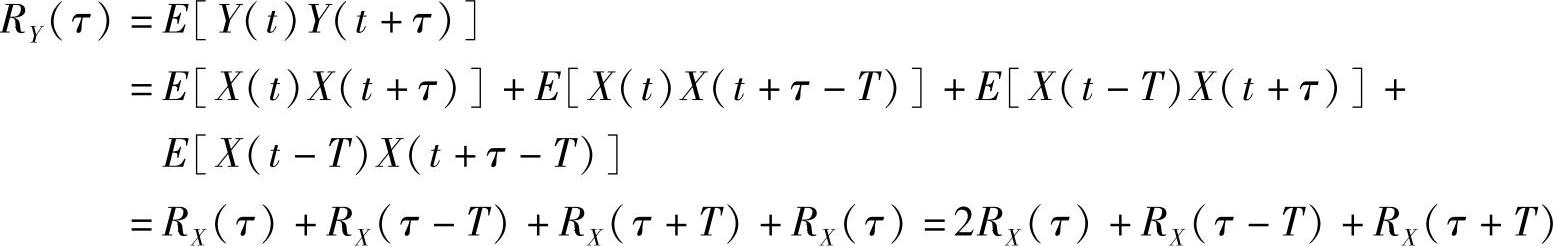
其傅里叶变换为Y（t）的功率谱，则

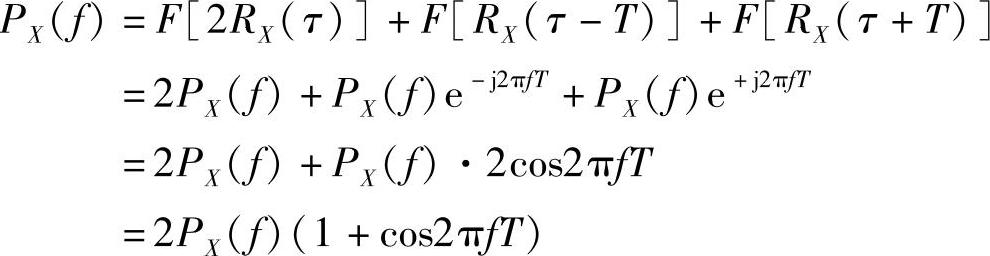
上式在推导过程中利用了R_X（τ）↔P_X（f）以及时延特性R_X（τ±T）↔P_X（f）e^±j2πfT。

方法二：设系统的输入信号和输出信号分别为x（t）和y（t），则由系统组成可得y（t）=x（t）+x（t-T），两边同时进行傅里叶变换，即

F[y（t）]=F[x（t）+x（t-T）]

Y（f）=X（f）+X（f）e^-j2πfT=X（f）[1+e^-j2πfT]

得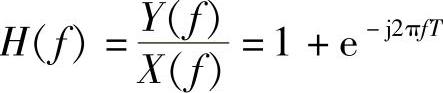

于是，根据平稳随机过程通过线性系统后功率谱的关系式得

P_Y（f）=P_X（f）|H（f）|²=P_X（f）|1+e^-j2πfT|²=2P_X（f）（1+cos2πfT）

21.试求与高斯脉冲信号

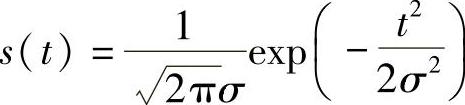
相匹配的匹配滤波器的传输特性和它能获得的最大输出信噪比。

解：（1）查常用函数傅里叶变换表，并做适当的代换得

S（f）=F[s（t）]=exp（-2π²σ²f²）

故与s（t）匹配的匹配滤波器的传输特性为

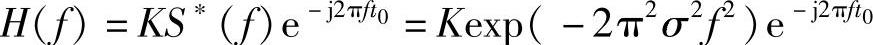
（2）输入信号s（t）的能量为

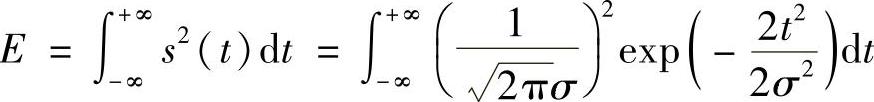
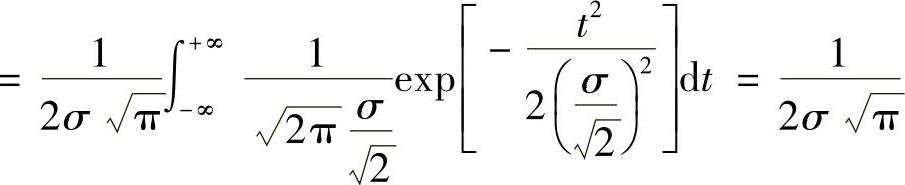
其中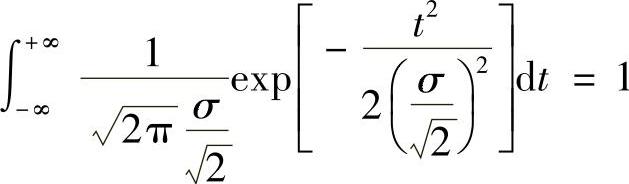，是服从正态分布的概率密度函数曲线下的面积。故匹配滤波器输出端的最大信噪比为

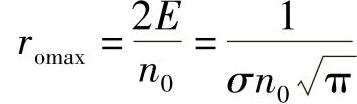
22.将图2-26所示的幅度为A伏、宽为τ₀秒的矩形脉冲加到与其相匹配的匹配滤波器上，则滤波器输出是一个三角形脉冲。

（1）求这个脉冲的峰值。

（2）如果把功率谱密度为n₀/2的白噪声加到此滤波器的输入端上，计算输出端上的噪声平均功率。

（3）设信号和白噪声同时出现于滤波器的输入端，试计算在信号脉冲峰值时的输出信噪比。

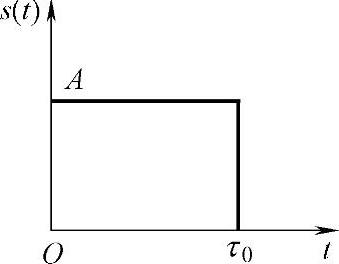
图2-26 矩形脉冲

解：（1）匹配滤波器输出为

s_o（t）=KR（t-t₀）

式中，K是任取的一个常数（为方便，一般令K=1）；R（t）是输入信号的自相关函数。故输出信号的最大值发生在t=t₀时刻（通常取t₀=τ₀），为

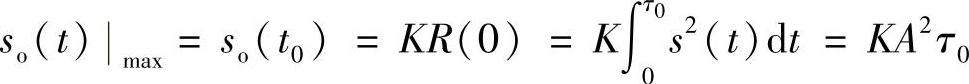
（2）在匹配滤波器型最佳接收机的性能推导中，需要求出白噪声通过匹配滤波器后的噪声功率。因此，本问题对接收机的性能分析有用。

方法一：求出输出噪声功率谱，对功率谱积分求得输出噪声平均功率。

匹配滤波器的传输特性为

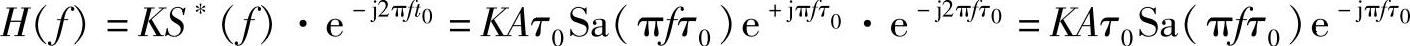
故匹配滤波器输出噪声功率谱为

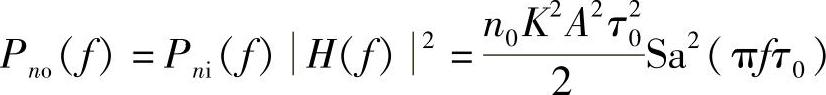
因此求得输出噪声的平均功率为

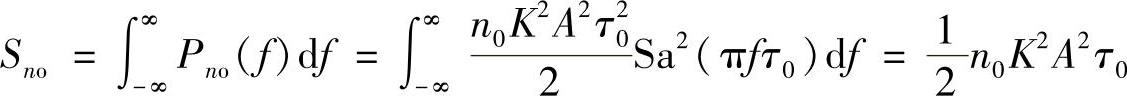
由帕塞瓦尔定理可知，式中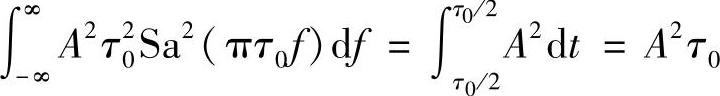是高度为A、宽度为τ₀的矩形脉冲的能量E。

方法二：用输出噪声时间表达式求出噪声方差，零均值噪声的方差即为平均功率。

设匹配滤波器的冲激响应为h（t），其输入噪声为n（t），则输出噪声为

输出噪声的平均功率为

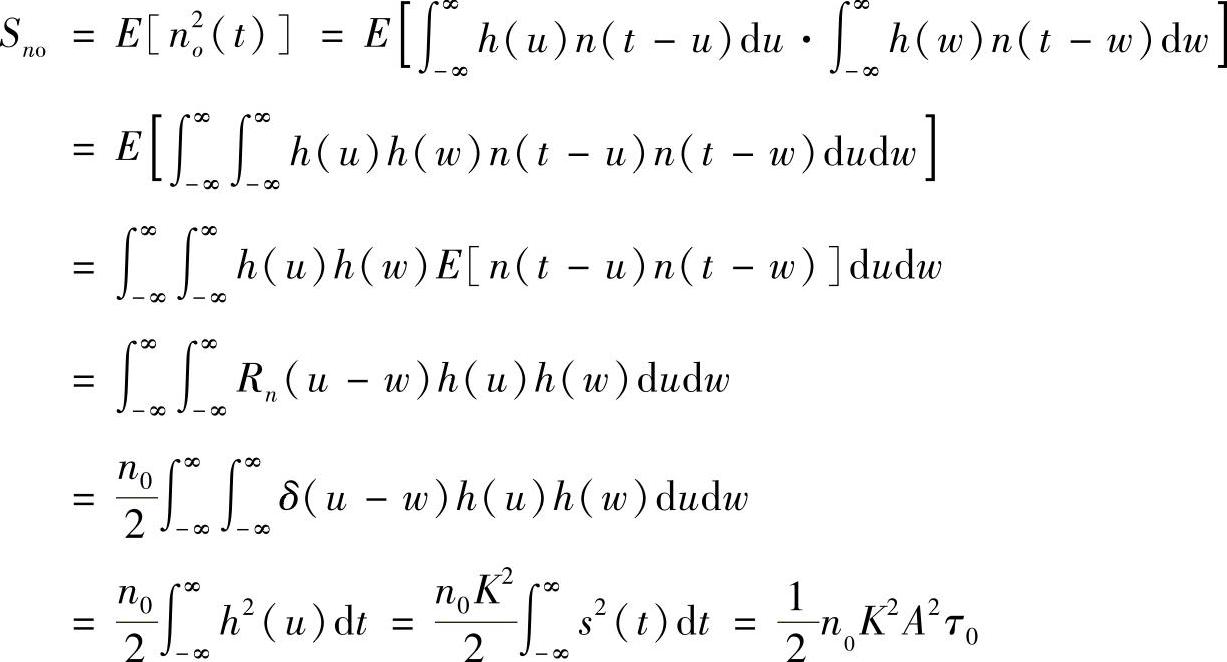
（3）信号脉冲峰值时的输出信噪比即为最大信噪比r_omax，有

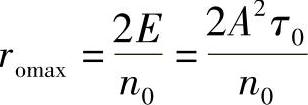
其中信号能量。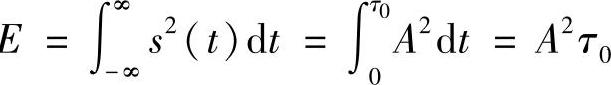

23.把上题的信号脉冲加到图2-27所示的RC网络上，设RC=2τ₀/3。

（1）画出输出脉冲，并与上题的结果相比较。

（2）若输入信号叠加了功率谱密度为n₀/2的白噪声，计算此时的输出噪声平均功率和输出端的峰值信噪比，并与上题的结果相比较。

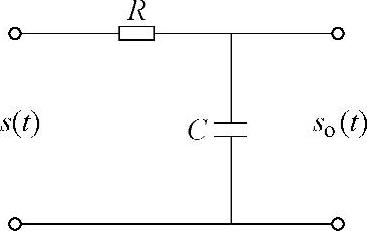
图2-27 RC网络

解：（1）此题用时域卷积求RC电路的输出信号更为容易。

RC电路的传输特性为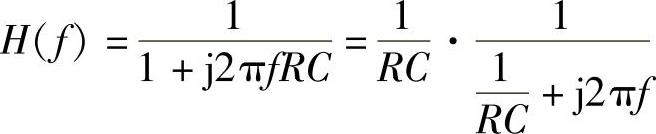

查常用函数傅里叶变换表得到其冲激响应表达式为

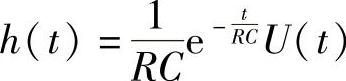
则RC电路的输出信号

s_o（t）=s（t）∗h（t）=A[U（t）-U（t-τ₀）]∗h（t）=AU（t）∗h（t）-AU（t-τ₀）∗h（t）利用教材例2-1所得结果，有

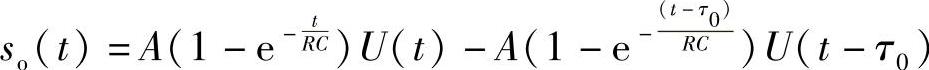
可见，此输出信号在t=τ₀达到最大值，最大值为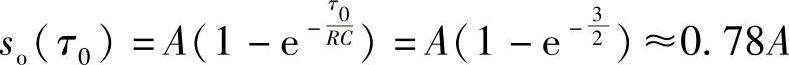输出脉冲如图2-28所示。

（2）参考教材中的例2-21，得输出噪声功率为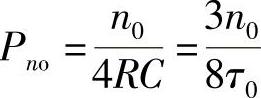

故输出峰值信噪比为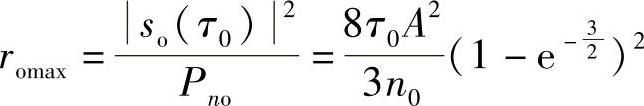

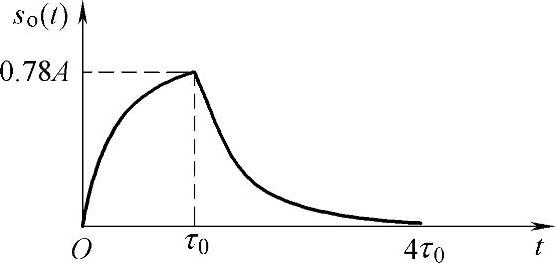
图2-28 输出脉冲示意图