高斯随机过程的特点及性质

高斯随机过程，又称正态随机过程。通信系统中的信道噪声多为高斯随机过程。

1.定义

任意n维概率密度函数服从高斯（正态）分布的随机过程。

2.重要性质

1）若高斯随机过程是广义平稳的，则它也是狭义平稳的。

2）若高斯随机过程的某两个取值（随机变量）互不相关，则这两个随机变量也是统计独立的。

3）多个高斯随机过程之和仍为高斯过程（数字特征可能会改变）。

4）高斯随机过程通过线性系统（或经线性变换）后仍为高斯过程（数字特征可能会改变）。

3.一维概率密度函数

尽管高斯随机过程的n维概率密度函数很复杂，但实际应用时用得最多的是一维概率密度函数。

（1）定义

高斯随机过程在任意时刻上的取值是一高斯随机变量，其概率密度函数为

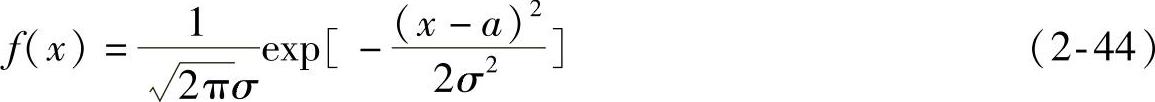
可以证明a为数学期望，σ²为方差，f（x）曲线如图2-3所示。

（2）特性

1）f（x）对称于x=a，在x→±∞时，f（x）→0。(www.xing528.com)

，显然。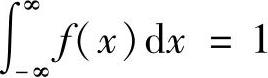

3）a是随机变量取值的分布中心，σ表示取值的集中程度。σ一定，改变a，则图形左右平移，形状不变；a一定，改变σ，图形将随着σ的减小而变高和变窄（曲线下的面积恒为1），但图形的中心位置不变。

4）当a=0、σ²=1时，称为标准正态分布，记为N（0，1）。

（3）两个特殊概率

当我们研究高斯噪声对数字通信的影响时，通常对图2-4a、图2-4b中阴影部分所对应的概率感兴趣。记住下面的结论会为推导数字系统的误码率带来方便。

图2-3 一维高斯概率密度函数

图2-4 两个有用的概率

1）当b＜a时，如图2-4a所示，阴影部分的概率为

2）当b＞a时，如图2-4b所示，阴影部分的概率为

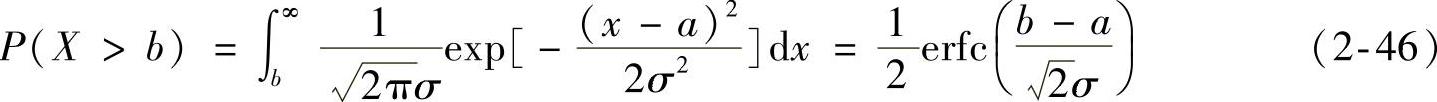
其中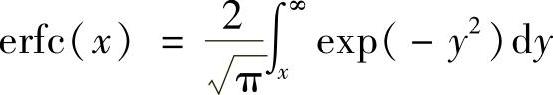称为误差补函数，其函数值可通过查表得到。