初学概率论：二维概率分布与密度函数

1.随机变量与概率分布

（1）随机变量

1）随机变量：以一定的概率取某些值的变量。

2）离散随机变量：随机变量可能的取值个数有限或无穷可数。

3）连续随机变量：随机变量可能的取值充满某一有限或无限区间。

（2）随机变量的概率分布

1）概率分布函数F（x）定义为

F（x）=P（X≤x） （2-27）

含义：随机变量X的取值小于或等于x的概率。如有离散随机变量X，分别以1/2的概率取2和6，则F（0.1）=P（X≤0.1）=0，F（2.1）=P（X≤2.1）=0.5，F（4）=P（X≤4）=0.5，F（6）=P（X≤6）=1

性质：

F（-∞）=P（X≤-∞）=0

F（∞）=P（X≤∞）=1

F（x）为单调不减函数，即如果x₁≤x₂，则有F（x₁）≤F（x₂）。

2）概率密度函数f（x）定义为

性质：

性质：

（3）二维概率分布函数和二维概率密度函数

单个随机变量的概率分布函数和概率密度函数称为一维概率分布函数和一维概率密度函数。两个随机变量的联合概率分布函数和联合概率密度函数则称为二维概率分布函数和二维概率密度函数。

1）二维概率分布函数定义为

F（x，y）=P（X≤x，Y≤y） （2-29）

含义：事件（X≤x）和事件（Y≤y）同时出现的概率。

2）二维概率密度函数定义为

（3）二维概率分布函数和二维概率密度函数

单个随机变量的概率分布函数和概率密度函数称为一维概率分布函数和一维概率密度函数。两个随机变量的联合概率分布函数和联合概率密度函数则称为二维概率分布函数和二维概率密度函数。

1）二维概率分布函数定义为

F（x，y）=P（X≤x，Y≤y） （2-29）

含义：事件（X≤x）和事件（Y≤y）同时出现的概率。

2）二维概率密度函数定义为

性质：

性质：

若f（x，y）=f（x）f（y），则称随机变量X与Y统计独立。

以上概念和结论可推广到其他多维概率分布函数和概率密度函数。本课程主要用到一维概率密度函数，偶尔涉及二维分布。

2.随机变量的数字特征

随机变量的数字特征有数学期望、方差、协方差（相关矩）和相关系数。

（1）数学期望

数学期望是随机变量的统计平均值，又称为均值，通常用a或m表示。

若f（x，y）=f（x）f（y），则称随机变量X与Y统计独立。

以上概念和结论可推广到其他多维概率分布函数和概率密度函数。本课程主要用到一维概率密度函数，偶尔涉及二维分布。

2.随机变量的数字特征

随机变量的数字特征有数学期望、方差、协方差（相关矩）和相关系数。

（1）数学期望

数学期望是随机变量的统计平均值，又称为均值，通常用a或m表示。

1）对于离散随机变量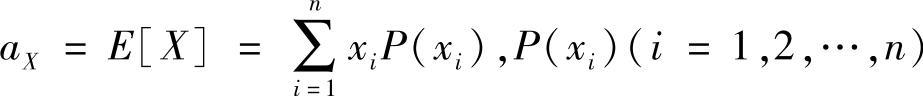：是随机变量X取x_i值的概率。

1）对于离散随机变量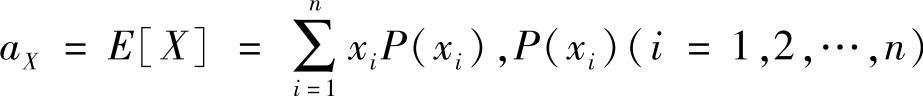：是随机变量X取x_i值的概率。

2）对于连续随机变量：是随机变量X的概率密度函数。

3）随机变量函数Y=g（X）的数学期望如下：

2）对于连续随机变量：是随机变量X的概率密度函数。

3）随机变量函数Y=g（X）的数学期望如下：

X为离散随机变量时：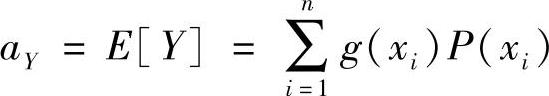

X为离散随机变量时：

X为连续随机变量时：

4）数学期望的常用性质如下：

E[C]=C，C为常数

E[X+Y]=E[X]+E[Y]

E[XY]=E[X]E[Y]，此式成立的条件是X、Y统计独立

E[X+C]=E[X]+C

E[CX]=CE[X](www.xing528.com)

（2）方差

方差表示随机变量取值的集中程度。方差越小，说明随机变量取值越集中，反之则越分散。方差通常用σ²表示，其平方根σ称为标准偏差。

X为连续随机变量时：

4）数学期望的常用性质如下：

E[C]=C，C为常数

E[X+Y]=E[X]+E[Y]

E[XY]=E[X]E[Y]，此式成立的条件是X、Y统计独立

E[X+C]=E[X]+C

E[CX]=CE[X]

（2）方差

方差表示随机变量取值的集中程度。方差越小，说明随机变量取值越集中，反之则越分散。方差通常用σ²表示，其平方根σ称为标准偏差。

1）对于离散随机变量：，a为随机变量的数学期望（均值）。

1）对于离散随机变量：，a为随机变量的数学期望（均值）。

2）对于连续随机变量：。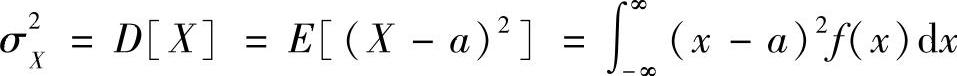

3）随机变量函数Y=g（X）的方差如下：

2）对于连续随机变量：。

3）随机变量函数Y=g（X）的方差如下：

X为离散随机变量：，a_Y是随机变量Y的均值

X为离散随机变量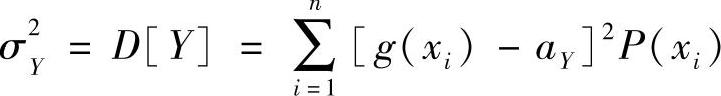：，a_Y是随机变量Y的均值

X为连续随机变量：

4）方差的性质如下：

D[C]=0，C为常数

D[X+Y]=D[X]+D[Y]，此式成立的条件是X、Y统计独立

D[X+C]=D[X]

D[CX]=C²D[X]

D[X]=E[X²]-E²[X]

如果X代表某随机电压，则此随机电压在1Ω电阻上消耗的功率为

X为连续随机变量：

4）方差的性质如下：

D[C]=0，C为常数

D[X+Y]=D[X]+D[Y]，此式成立的条件是X、Y统计独立

D[X+C]=D[X]

D[CX]=C²D[X]

D[X]=E[X²]-E²[X]

如果X代表某随机电压，则此随机电压在1Ω电阻上消耗的功率为

式中，E²[X]=a²为直流功率；D[X]=σ²为交流功率。

（3）协方差、相关矩和相关系数

两个随机变量X、Y的协方差定义为

Cov（X，Y）=E[（X-a_X）（Y-a_Y）]=E[XY]-a_Xa_Y （2-32）

两个随机变量X、Y之间的相关矩定义为

式中，E²[X]=a²为直流功率；D[X]=σ²为交流功率。

（3）协方差、相关矩和相关系数

两个随机变量X、Y的协方差定义为

Cov（X，Y）=E[（X-a_X）（Y-a_Y）]=E[XY]-a_Xa_Y （2-32）

两个随机变量X、Y之间的相关矩定义为

两个随机变量X、Y的相关系数反映了它们之间的相关程度，定义如下：

两个随机变量X、Y的相关系数反映了它们之间的相关程度，定义如下：

需要注意如下三个重要概念：

当协方差Cov（XY）=0时，相关系数ρ=0，则称两个随机变量是不相关的。

当相关矩E[XY]=0时，称两个随机变量是正交的。

当两个随机变量的联合概率密度函数等于两个随机变量各自概率密度函数的乘积，即f（x，y）=f（x）f（y）时，称两个随机变量是独立的。独立与不相关的关系：独立的两个随机变量一定是不相关的，而不相关的两个随机变量不一定独立。只有当两个随机变量服从高斯分布时，不相关的两个随机变量也一定是独立的。

需要注意如下三个重要概念：

当协方差Cov（XY）=0时，相关系数ρ=0，则称两个随机变量是不相关的。

当相关矩E[XY]=0时，称两个随机变量是正交的。

当两个随机变量的联合概率密度函数等于两个随机变量各自概率密度函数的乘积，即f（x，y）=f（x）f（y）时，称两个随机变量是独立的。独立与不相关的关系：独立的两个随机变量一定是不相关的，而不相关的两个随机变量不一定独立。只有当两个随机变量服从高斯分布时，不相关的两个随机变量也一定是独立的。