波形相关性的研究及应用

波形的相关是研究波形间相关程度的。波形间的相关程度可用相关函数和相关系数来表示。

1.相关函数

相关函数分为互相关函数和自相关函数。

（1）互相关函数的定义

周期信号v₁（t）和v₂（t）间的互相关函数R₁₂（τ）定义为

非周期功率信号v₁（t）和v₂（t）间的互相关函数R₁₂（τ）定义为

非周期功率信号v₁（t）和v₂（t）间的互相关函数R₁₂（τ）定义为

能量信号v₁（t）和v₂（t）间的互相关函数R₁₂（τ）定义为

能量信号v₁（t）和v₂（t）间的互相关函数R₁₂（τ）定义为

互相关函数的特点：

1）若对所有τ，都有R₁₂（τ）=0，则两个信号互不相关。

2）R₁₂（τ）=R₂₁（-τ）。

（2）自相关函数的定义

当v₁（t）=v₂（t）时，互相关函数即为自相关函数。

互相关函数的特点：

1）若对所有τ，都有R₁₂（τ）=0，则两个信号互不相关。

2）R₁₂（τ）=R₂₁（-τ）。

（2）自相关函数的定义

当v₁（t）=v₂（t）时，互相关函数即为自相关函数。

周期信号v（t）的自相关函数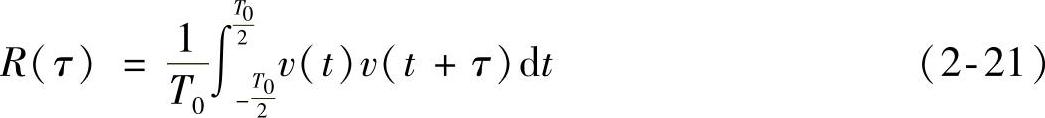

周期信号v（t）的自相关函数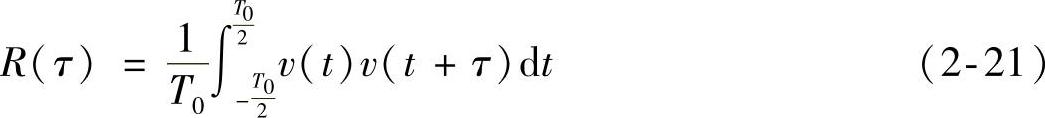

非周期功率信号v（t）的自相关函数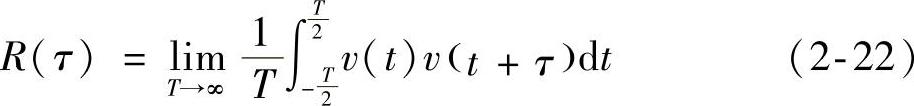

非周期功率信号v（t）的自相关函数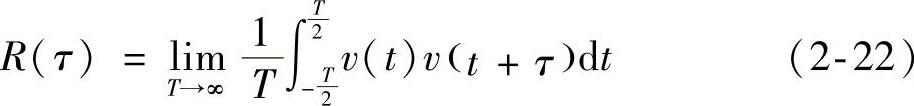

能量信号v（t）的自相关函数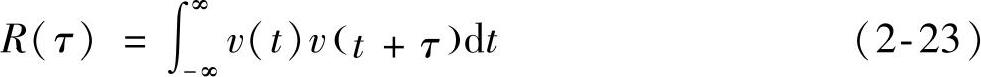

自相关函数的特点：

1）R（τ）是偶函数，即R（τ）=R（-τ）。(www.xing528.com)

2）R（0）≥R（τ）。R（0）有特殊意义，功率信号的R（0）等于信号的平均功率，能量信号的R（0）等于信号的总能量。

3）周期信号的R（τ）也是周期性的，且其周期与信号周期相同。

4）自相关函数与能量谱密度或功率谱密度之间是一对傅里叶变换的关系，即

对能量信号 R（τ）↔G（f） （2-24）

对功率信号 R（τ）↔P（f） （2-25）

2.互相关系数

v₁（t）和v₂（t）的互相关系数定义为

能量信号v（t）的自相关函数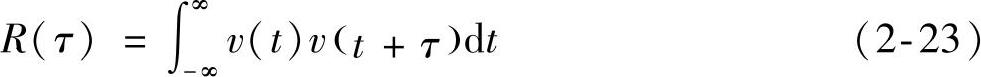

自相关函数的特点：

1）R（τ）是偶函数，即R（τ）=R（-τ）。

2）R（0）≥R（τ）。R（0）有特殊意义，功率信号的R（0）等于信号的平均功率，能量信号的R（0）等于信号的总能量。

3）周期信号的R（τ）也是周期性的，且其周期与信号周期相同。

4）自相关函数与能量谱密度或功率谱密度之间是一对傅里叶变换的关系，即

对能量信号 R（τ）↔G（f） （2-24）

对功率信号 R（τ）↔P（f） （2-25）

2.互相关系数

v₁（t）和v₂（t）的互相关系数定义为

讨论：

1）当v₁（t）=v₂（t）时，R₁₂（0）=R₁₁（0）=R₂₂（0），代入上式得ρ₁₂=1，为自相关系数。

2）当v₁（t）=-v₂（t）时，R₁₂（0）=-R₁₁（0）=-R₂₂（0），得ρ₁₂=-1。

3）-1≤ρ₁₂≤1，当ρ₁₂=0时，称v₁（t）与v₂（t）不相关。

讨论：

1）当v₁（t）=v₂（t）时，R₁₂（0）=R₁₁（0）=R₂₂（0），代入上式得ρ₁₂=1，为自相关系数。

2）当v₁（t）=-v₂（t）时，R₁₂（0）=-R₁₁（0）=-R₂₂（0），得ρ₁₂=-1。

3）-1≤ρ₁₂≤1，当ρ₁₂=0时，称v₁（t）与v₂（t）不相关。