确知信号的频谱分析技术优化

确知信号可分为周期信号和非周期信号。

若x（t）=x（t+T₀）对于任何t值成立，其中T₀为满足此关系式的最小值，则称x（t）为周期信号，T₀为周期。否则称x（t）为非周期信号。

确知信号的频谱分析方法：周期信号——傅里叶级数展开；非周期信号——傅里叶变换。

通过频谱分析可以知道信号所包含的频率成分、各频率成分幅度、相位大小和主要频率成分占据的频带宽度及位置。

1.周期信号的频谱分析——傅里叶级数展开

周期为T₀的周期信号x（t），且满足狄里赫利条件（一般实际信号均满足），则x（t）可展开成如下的指数型傅里叶级数：

其中，傅里叶级数的系数为

式中，f₀=1/T₀称为信号的基频，基频的n倍（n为整数，-∞＜n＜+∞）称为n次谐波频率。当n=0时，有

它表示信号的时间平均值，即直流分量。

当x（t）为实偶信号时，V_n为实偶函数。V_n反映了周期信号中各次谐波的幅度值和相位值，V_n～f称为周期信号的频谱，|V_n|～f称为振幅谱。

例如，周期矩形脉冲序列和周期冲激脉冲序列的时域波形分别如图2-1a、图2-1b所示。按式（2-2）分别求得

对于周期矩形脉冲序列：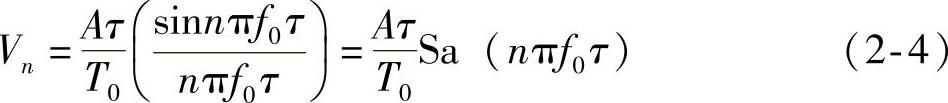

对于周期冲激脉冲序列：

对应的V_n～f分别如图2-1c、图2-1d所示。

图2-1 周期信号频谱实例

由此可见，周期信号的频谱有如下特点：

1）离散性。V_n只在f=nf₀（n=0，±1，±2，…，整数）时才有值，因此周期信号的频谱由离散的谱线组成，谱线间隔为f₀=1/T₀。

2）谐波性。谱线位置都在f=nf₀处，nf₀称为基波f₀的n次谐波，故称周期信号的频谱具有谐波性。

2.非周期信号的频谱分析——傅里叶变换

（1）傅里叶变换

称X（f）为x（t）的频谱。当X（f）是复函数时，X（f）=|X（f）|e^-jϕ（f），其中|X（f）|～f称为振幅谱，ϕ（f）～f称为相位谱。

X（f）具有如下特点：

1）X（f）是连续谱。

2）X（f）与x（t）之间一一对应，记为x（t）↔X（f）。

3）当x（t）是实偶函数时，X（f）是实偶函数，可直接画出频谱X（f）～f。

（2）傅里叶变换的常用运算特性

1）线性叠加：(www.xing528.com)

F[Ax₁（t）+Bx₂（t）]=AF（x₁（t））+BF（x₂（t）） （2-8）

2）对偶性：

若 X（f）=F[x（t）]

则 F[X（t）]=x（-f） （2-9）

3）时移特性：

若 X（f）=F[x（t）]

则

4）频移特性：

若 X（f）=F[x（t）]

则

5）调制特性：

若 X（f）=F[x（t）]

则

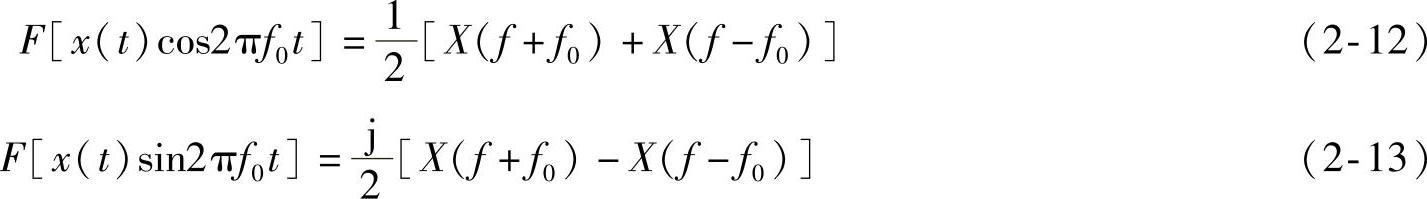
6）卷积特性：

若 X（f）=F[x（t）]和Y（f）=F[y（t）]

则 F[（x（t）∗y（t）]=X（f）Y（f）——时域卷积，频域相乘 （2-14）

F[（x（t）y（t）]=X（f）∗Y（f）——时域相乘，频域卷积 （2-15）

说明：卷积运算通常很烦，但当其中一个函数为冲激函数（或冲激序列函数）时，卷积运算会变得十分简便。如x（t）∗δ（t-t₀）=x（t-t₀），X（f）∗δ（f-f_c）=X（f-f_c）。

（3）常用信号的傅里叶变换

为便于使用，将“通信原理”课程中可能用到的傅里叶变换列于表2-1中。表中前6个变换对后续学习十分重要，应熟记它们的表达式、波形形状以及波形图上的各关键参数（如纵坐标上的最大值、第一个零点位置、零点之间的间隔等）。

表2-1 常用信号的傅里叶变换

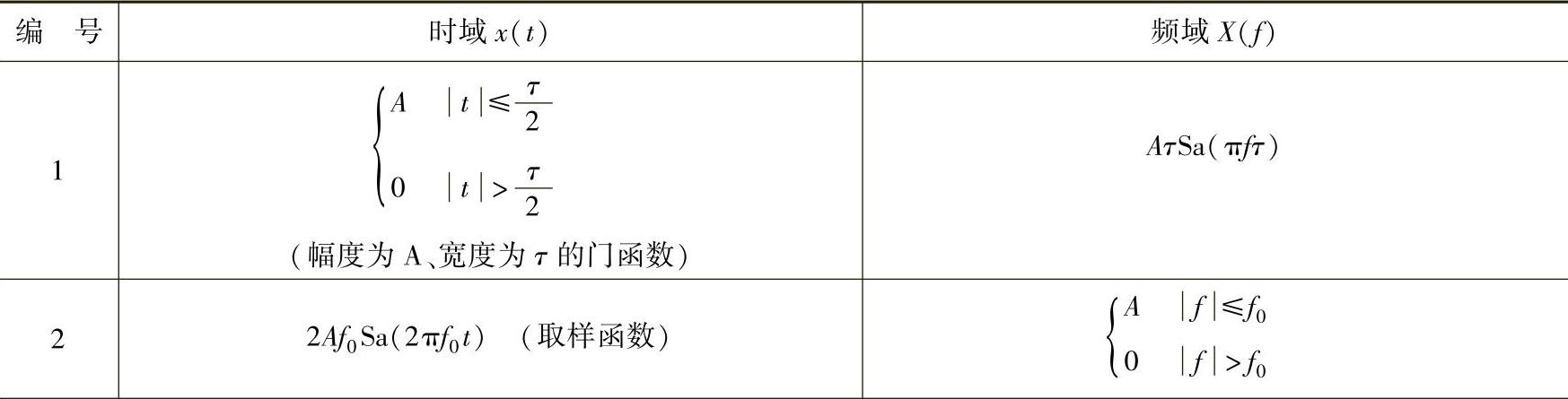
（续）

（续）

（续）