如何计算误比特率和误码率？

1.设A系统为二进制传输系统，码元速率为2000Baud，占用信道带宽为2000Hz；B系统为四进制传输系统，码元速率为1000Baud，占用信道带宽为1000Hz。试问：A、B两个系统哪个系统的有效性更高？

解：信息频带利用率能准确反映系统的有效性。

A系统：信息传输速率 R_b=R_slog₂M=（2000×log₂2）bit/s=2000bit/s

频带利用率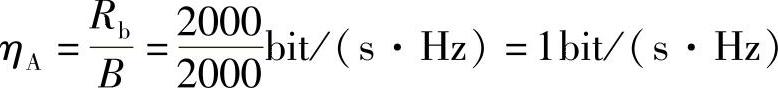

B系统：信息传输速率 R_b=R_slog₂4=（1000×log₂4）bit/s=2000bit/s

频带利用率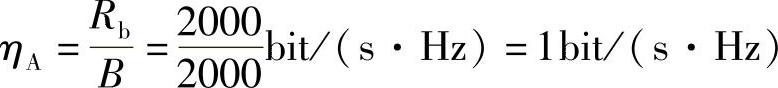

B系统：信息传输速率 R_b=R_slog₂4=（1000×log₂4）bit/s=2000bit/s

频带利用率为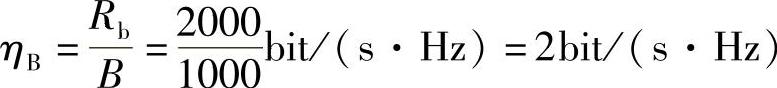

所以，B系统的有效性更高。

评注：尽管码元速率、信息速率、码元频带利用率、信息频带利用率都可用来衡量系统的有效性，但前三者都需要特定的条件。例如，若进制相同且占用相同的带宽，则码元速率越高的系统其有效性越高；若占用相同的系统带宽，则信息传输速率越高的系统其有效性越高；若进制相同，则码元频带利用率越高，系统的有效性越高。所以，衡量不同系统的有效性，最准确的指标是信息频带利用率。

2.某信息源输出A、B、C、D四种符号，独立等概，传输时每个符号用两位二进制码表示，如A：00，B：01，C：10，D：11。已知信息传输速率R_b=1Mbit/s，试求

（1）该信源输出的码元速率。

（2）该信息源工作1h发出的信息量。

（3）若在1h内收到的信息中，大致均匀地发现了36bit的错误信息，求误比特率和误码（符号）率。

解：（1）该信源是四进制信源，即M=4，且独立等概，故由信息速率即可求得码元速率为

频带利用率为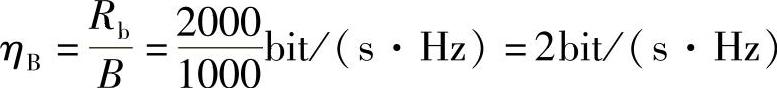

所以，B系统的有效性更高。

评注：尽管码元速率、信息速率、码元频带利用率、信息频带利用率都可用来衡量系统的有效性，但前三者都需要特定的条件。例如，若进制相同且占用相同的带宽，则码元速率越高的系统其有效性越高；若占用相同的系统带宽，则信息传输速率越高的系统其有效性越高；若进制相同，则码元频带利用率越高，系统的有效性越高。所以，衡量不同系统的有效性，最准确的指标是信息频带利用率。

2.某信息源输出A、B、C、D四种符号，独立等概，传输时每个符号用两位二进制码表示，如A：00，B：01，C：10，D：11。已知信息传输速率R_b=1Mbit/s，试求

（1）该信源输出的码元速率。

（2）该信息源工作1h发出的信息量。

（3）若在1h内收到的信息中，大致均匀地发现了36bit的错误信息，求误比特率和误码（符号）率。

解：（1）该信源是四进制信源，即M=4，且独立等概，故由信息速率即可求得码元速率为

（2）信息速率乘以时间长度等于这段时间内的信息量，故1h内发出的信息量为

I=R_bT=（1×10⁶×60×60）bit=3.6×10⁹bit

（3）根据误比特率定义得

（2）信息速率乘以时间长度等于这段时间内的信息量，故1h内发出的信息量为

I=R_bT=（1×10⁶×60×60）bit=3.6×10⁹bit

（3）根据误比特率定义得

码元速率乘以时间长度即为码元总数，故1h内传输的总码元（符号）数为

N=R_sT=（5×10⁵×3600）个=1.8×10⁹个

由于一个四进制码元由两个二进制码元组成，在独立等概时，每个二进制码元携带1bit信息。已知这36bit的错误信息均匀分散在接收信息中，可认为36bit的错误导致36个四进制码元发生错误，即每个四进制码元中只有一位二进制码元错误。因此，此四进制系统的误码率为

码元速率乘以时间长度即为码元总数，故1h内传输的总码元（符号）数为

N=R_sT=（5×10⁵×3600）个=1.8×10⁹个

由于一个四进制码元由两个二进制码元组成，在独立等概时，每个二进制码元携带1bit信息。已知这36bit的错误信息均匀分散在接收信息中，可认为36bit的错误导致36个四进制码元发生错误，即每个四进制码元中只有一位二进制码元错误。因此，此四进制系统的误码率为

评注：在多进制系统中，想确切得到误码率与误比特率的关系几乎是不可能的，因为很难知道错误比特的分布规律。在误比特率较低时，可看成错误比特分散在各个多进制码元中，1bit信息的错误导致一个多进制码元的错误（或一个码元中只错1bit），从而得到误码率与误比特率之间的近似关系式为

P_b=P_e/log₂M

这虽然是近似，但与实际情况较接近。

3.某系统采用脉冲组形式传输信息。每个脉冲组包含4个信息脉冲和1个休止脉冲。每个脉冲的宽度为1ms，信息脉冲选自脉冲集，脉冲集中的脉冲共有16种，且16种脉冲等概出现，求码元（脉冲）速率和平均信息速率。(www.xing528.com)

解：（1）每个脉冲的宽度为T_s=1ms，故

评注：在多进制系统中，想确切得到误码率与误比特率的关系几乎是不可能的，因为很难知道错误比特的分布规律。在误比特率较低时，可看成错误比特分散在各个多进制码元中，1bit信息的错误导致一个多进制码元的错误（或一个码元中只错1bit），从而得到误码率与误比特率之间的近似关系式为

P_b=P_e/log₂M

这虽然是近似，但与实际情况较接近。

3.某系统采用脉冲组形式传输信息。每个脉冲组包含4个信息脉冲和1个休止脉冲。每个脉冲的宽度为1ms，信息脉冲选自脉冲集，脉冲集中的脉冲共有16种，且16种脉冲等概出现，求码元（脉冲）速率和平均信息速率。

解：（1）每个脉冲的宽度为T_s=1ms，故

（2）每5个脉冲中有4个信息脉冲，只有信息脉冲才携带信息。16种信息脉冲等概出现，每个信息脉冲携带的信息量为I=log₂M=log₂16bit=4bit，故信息传输速率为

（2）每5个脉冲中有4个信息脉冲，只有信息脉冲才携带信息。16种信息脉冲等概出现，每个信息脉冲携带的信息量为I=log₂M=log₂16bit=4bit，故信息传输速率为

4.某信源产生a、b、c、d4种符号，各符号独立出现。

（1）4种符号的出现概率分别为1/2、1/4、1/8、1/8，试求该信源的熵。

（2）4种符号等概出现时，求信源的熵。

解：由题意及式（1-2）可得信源熵为

4.某信源产生a、b、c、d4种符号，各符号独立出现。

（1）4种符号的出现概率分别为1/2、1/4、1/8、1/8，试求该信源的熵。

（2）4种符号等概出现时，求信源的熵。

解：由题意及式（1-2）可得信源熵为

（2）4种符号等概时，每个符号的概率均为1/4，所以信源熵为

（2）4种符号等概时，每个符号的概率均为1/4，所以信源熵为

强调：当信源的各种符号等概时，信源熵达到最大log₂Mbit/符号。故二进制信源最大熵为1bit/符号，四进制信源最大熵为2bit/符号，八进制为3bit/符号，十六进制为4bit/符号。

5.一幅黑白图像含有4×10⁵个像素，设每个像素有16个等概率出现的亮度等级。

（1）试求每幅黑白图像的平均信息量。

（2）若每秒钟传输24幅黑白图像，其信息速率为多少？

解：（1）由题意，每个像素的平均信息量为

H=log₂M=log₂16=4bit/像素

故一幅黑白图像的平均信息量为

I=（4×10⁵×4）bit=1.6×10⁶bit

（2）当每秒传输24幅黑白图像时，信息速率为

R_b=24×I=（24×1.6×10⁶）bit/s=3.84×10⁷bit/s

强调：当信源的各种符号等概时，信源熵达到最大log₂Mbit/符号。故二进制信源最大熵为1bit/符号，四进制信源最大熵为2bit/符号，八进制为3bit/符号，十六进制为4bit/符号。

5.一幅黑白图像含有4×10⁵个像素，设每个像素有16个等概率出现的亮度等级。

（1）试求每幅黑白图像的平均信息量。

（2）若每秒钟传输24幅黑白图像，其信息速率为多少？

解：（1）由题意，每个像素的平均信息量为

H=log₂M=log₂16=4bit/像素

故一幅黑白图像的平均信息量为

I=（4×10⁵×4）bit=1.6×10⁶bit

（2）当每秒传输24幅黑白图像时，信息速率为

R_b=24×I=（24×1.6×10⁶）bit/s=3.84×10⁷bit/s