教材习题详解：信息速率与码元速率的求解方法

1.某信源符号集由A、B、C、D、E、F组成，设每个符号独立出现，其概率分别为1/4、1/4、1/16、1/8、1/16、1/4，试求该信息源输出符号的平均信息量。

解：用离散信源熵的计算式（1-2）得

2.国际莫尔斯电码用“点”和“划”的序列发送英文字母，“点”用持续一单位的电流脉冲表示，“划”用持续三单位的电流脉冲表示，且“划”出现的概率是“点”出现概率的1/3，求：

（1）“点”和“划”的信息量。

（2）“点”和“划”的平均信息量。

解：（1）“划”出现的概率是“点”出现概率的1/3，即P₁=（1/3）P₂，且P₁+P₂=1，所以P₁=1/4，P₂=3/4。故有

“划”的信息量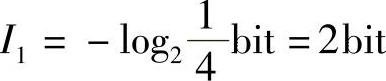

独立等概时，四进制信源的熵H=log₂4bit/符号=2bit/符号，故平均信息速率

R_b=R_s·H=（100×2）bit/s=200bit/s

（2）各个符号的出现不等概时，信源熵和平均信息速率分别为

“点”的信息量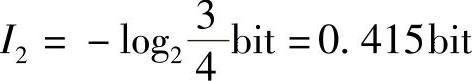

（2）平均信息量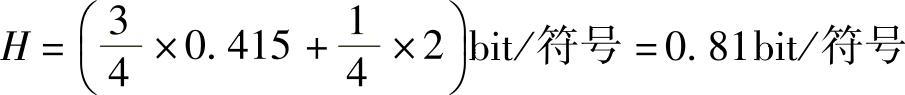

3.设一数字传输系统传送二进制码元的速率为2400Baud，试求该系统的信息速率。若该系统改为传送十六进制信号码元，码元速率不变，则这时的系统信息速率是多少（设各码元独立等概出现）？

解：（1）M=2，R_s=2400Baud，信息速率为

R_b=R_slog₂M=2400×log₂2bit/s=2400bit/s

（2）M=16，R_s=2400Baud，信息速率为

R_b=R_slog₂M=2400×log₂16bit/s=9600bit/s

可见，当码元速率相同时，多进制系统的信息速率更高。在以后的学习中会发现，信号传输时占用信道带宽与码元速率有关。所以多进制系统具有更高的有效性。

4.某信息源的符号集由A、B、C、D组成，对于传输的每一个符号用二进制脉冲编码表示，00对应A，01对应B，10对应C，11对应D，每个二进制脉冲的宽度为5ms。假设每一符号独立出现。(www.xing528.com)

（1）不同符号等概率出现时，试计算传输的平均信息速率。

（2）若每个符号出现的概率分别为P_A=1/5，P_B=1/4，P_C=1/4，P_D=3/10，试计算传输的平均信息速率。

解：（1）信源符号共有4种，是四进制信源。每个符号用两位二进制码表示，每个二进制码元宽度为5ms，故一个四进制信源符号占据的时间宽度为T_s=10ms，所以四进制信源的符号速率为

独立等概时，四进制信源的熵H=log₂4bit/符号=2bit/符号，故平均信息速率

R_b=R_s·H=（100×2）bit/s=200bit/s

（2）各个符号的出现不等概时，信源熵和平均信息速率分别为

5.已知某四进制数字传输系统的信息传输速率为2400bit/s，接收端在半个小时内共收到216个错误码元，试计算该系统的误码率P_e。

5.已知某四进制数字传输系统的信息传输速率为2400bit/s，接收端在半个小时内共收到216个错误码元，试计算该系统的误码率P_e。

解：根据误码率公式，已知半小时内收到的错误码元数为216个，故只要求出半小时内传输的总码元数即可。总码元数等于码元速率与时间长度的乘积。

由信息速率可求出码元速率为

解：根据误码率公式，已知半小时内收到的错误码元数为216个，故只要求出半小时内传输的总码元数即可。总码元数等于码元速率与时间长度的乘积。

由信息速率可求出码元速率为

半小时内传输的总码元数为

N=R_st=（1200×30×60）个=2.16×10⁶个

求得误码率为

半小时内传输的总码元数为

N=R_st=（1200×30×60）个=2.16×10⁶个

求得误码率为