热容量系数与流化床的层数分析

7.2.5.1　热容量系数

在干燥过程的计算中,采用传热或传质速率积分式均可以求出所需的设备容积,然而,考虑到传热系数比传质系数更容易获得,而且精度也更高,故往往采用传热速率式进行计算。多层流化床中的传热速率式可写为

式中,Q为传热速率,W;A为流化床截面积,m2;Δtm为物料与气体之间的对数平均温差,℃;K为流体与颗粒间的传热系数,W/(m2·℃)。

在流化床计算中,K一般表示为以流化床颗粒质量为基准的传热系数,称为热容量系数,并可表示为

式中,α为流体与颗粒间的给热系数,W/(m2·℃);a为单位质量颗粒的有效传热面积,m2/kg;h0为多层流化床物料存留量,kg/m2床截面。

在求取热容量系数的过程中,对于流化床中流体与颗粒间的传热机理,曾提出了各种不同的模型来加以说明,其中如Zabrod-sky的“微隙模型”(Microbreak Model),此模型认为过剩气体(超过临界流化需要量的气体)短路通过一排或数排固体颗粒,然后再与渗过颗粒层的气体完全混合,此过程一再重复通过整个床层。Kunii Levenspiel提出了“鼓泡床模型”(Bubbles Bed Model)来预测流化床中气体与颗粒间的传热系数。根据此模型,气体与颗粒间的传热分成两部分进行:一部分是在气泡内由气体将热量传递给颗粒,另一部分是由气体在气泡和气泡晕间的交换而将热量由气泡传递给气泡晕。Kato和Wen则提出了“气泡汇合模型”(Bubble Assemblage Model)。此模型把流化床沿高度分成若干段,每一段的高度相当于在此段中的气泡大小,然后逐段计算。

这些模型都有一定的局限性。实际上,流化床中流体与颗粒间的传热是很复杂的,特别是如果还伴有内部热阻、化学反应,或存在着对床的辐射热流时,情况更为复杂。所以难以给出过程的数学描述。为此,许多研究者大抵应用下列两种方法之一。

(1)往往用量纲一的数群来整理实验结果而不将其归结到任一特定的物理模型。

(2)确定模型,并由此整理实验结果。这种选择的准确性决定于实验条件下模型本身的真实程度。

对于砂子、矾土、炭粉和矿渣等物料,用多孔板多层流化床进行表面蒸发期间的干燥实验所获得的热容量系数经验式可表示为:

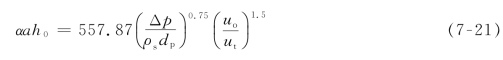
上式适用范围为:

0.6 mm＜dp＜1.4 mm

1.0＜uo/ut＜2.2

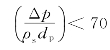
需要指出的是,不同研究者所得出的传热系数间差别是很大的,即使对于同一个Re,也可能存在数十倍之差。因此,应该特别注意的是,某一关联式往往只对同一种型式的设备才是适用的。

7.2.5.2　流化床的层数

1)干燥区间

在此期间物料温度等于与之接触的热风的湿球温度tw,且为一定值。在略去热损失的条件下,热风所给出的热量全部用于物料水分在湿球温度下的蒸发。

如图7-13所示,设干燥区间有n层,进入n层的热风温度为tn,进入(n-1)层的热风温度为tn-1,则第n层的传热量Qn为

式中,cpH为湿空气的比热容,cpH=cpg+cpvH,J/(kg干气,℃)。

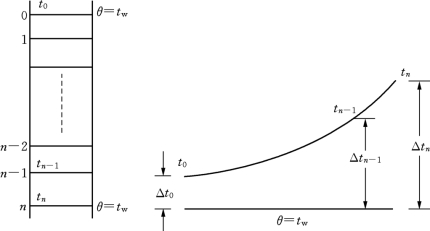
图7-13　干燥区间温度分布

其传热速率式为:

合并式(7-22)、式(7-23)得:

令tn-tw=Δtn,tn-1-tw=Δtn-1,

由于在一定的操作条件下,α,a,h0,A,V,cpH均为定值,即

则式(7-24)可写成

Δtn/Δtn-1=K1

同理,对(n-1)层作热平衡及给热速率关联,可得:

Δtn-1/Δtn-2=K1(www.xing528.com)

依此类推,最后一层

Δt1/Δt0=K1

将上述各关系式的左、右两边数值各自相乘可得

将式(7-25)代回式(7-26)并将式两边各取对数,得

整理得

由上式可根据热容量系数求得干燥区间所需要的流化床层数。

2)物料预热或升温区间

在预热阶段,热风所提供的热量是用于对物料加热,使之由进口温度θ1预热至tw。

而在升温阶段,考虑到物料分散悬浮时其临界湿含量Xc一般均较小,因此忽略水分在升温阶段的蒸发潜热,同样可认为热风所提供的热量完全用于使物料由tw升温到物料的出口温度θ2。

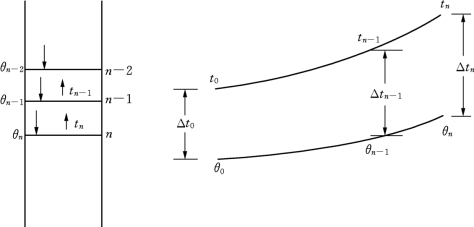
图7-14　物料预热或升温区间的温度分布

如图7-14所示,对第n层作热量衡算

其传热速率式为:

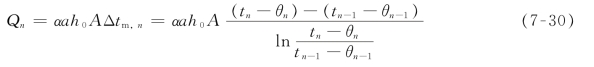
令

tn-θn=Δtn

tn-1-θn-1=Δtn-1

合并式(7-29)、式(7-30)可得:

将式(7-31)、式(7-32)等号两边相减,

所以

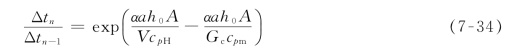
令

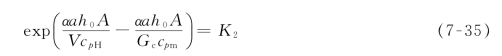
则

Δtn/Δtn-1=K2,Δtn-1/Δtn-2=K2,…,Δt1/Δt0=K2

将上述关系式的左、右两边各项各自相乘可得

将式(7-35)的K2值代回式(7-36)并各取对数得:

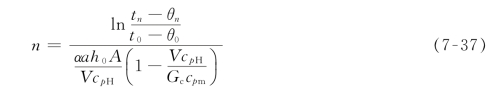
由式(7-37)可根据热容量系数求得物料预热或升温区间所需要的流化床层数。