用活塞流模型计算塔高的方法优化

5.3.3.1　传质单元数和传质单元高度

影响传质速率的另一重要因素是传质推动力。当工艺条件一定时,与其他接触方式相比,两相逆流接触时的传质推动力最大。因此在转盘塔中,料液和萃取剂逆流流动,并在连续逆流过程中进行传质。图5-11是转盘塔物流的示意图。设萃余相的流量为R(m3/s),萃取相的流量为E(m3/s),萃余相和萃取相的浓度分别为x和y(kmol/m3)。

活塞流模型假定两相在塔内做活塞流流动,即每一相在塔内同一截面上,各处的流速都相等,就像活塞一样,平行有规则地向前推进。并假定溶质在两相间的传递仅发生在水平方向上,而在垂直方向上,每一相内都不发生传质。

以塔顶为基准面计算塔高L。设塔内任意高度Z处的两相浓度分别为x和y,在高度为dZ的微塔段内作物料衡算,被萃取组分在dZ内的传递速率为:

根据传质速率方程式又可以得:

式中,a为传质比表面,m2/m3;A为塔的横截面积,m2;xe为与萃取相浓度y平衡的萃余相浓度;ye为与萃余相浓度x平衡的萃取相浓度。

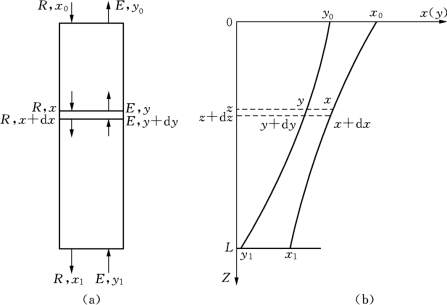
图5-11　转盘塔的活塞流模型

对于定态传质过程,两相在塔内任意点的浓度保持恒定,因此从式(5-36)和式(5-37)可得:

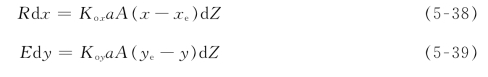
即:

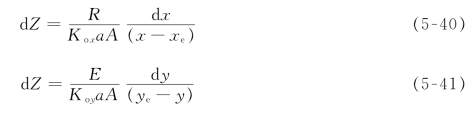
若萃余相的进口和出口浓度分别为x0和x1,萃取相的进口和出口浓度分别为y1和y0。为完成此分离任务所需要的塔高可以对上两式进行积分得到。对于两相互不相溶的稀溶液,R和E可视为常数。假定全塔中Koxa和Koya为常数,则塔高可分别用下列两式进行计算:

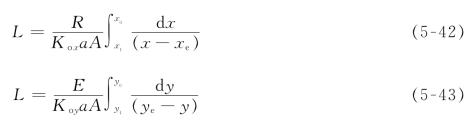
若令

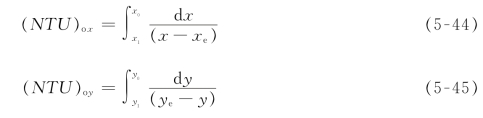
则塔高可表示为:

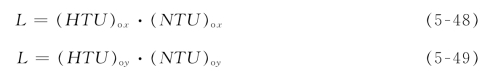
以上各式中的L为塔高,(HTU)ox和(HTU)oy称传质单元高度,是转盘塔分离效能高低的反映,具体数值须由实验测定;(NTU)ox和(NTU)oy称传质单元数,反映了分离任务的难易。以下介绍传质单元数的计算方法。

5.3.3.2　传质单元数的计算

在两相不互溶或萃取过程中每一相体积流量无明显变化的情况下,R、E可视为常数。此时NTU值的计算较为简单。

1)平衡线为直线的情况

这是最简单的情况,根据平衡关系可写成:

(www.xing528.com)

根据物料衡量,可导出任一塔截面上两相浓度之间的关系,即操作线方程为:

将上面两式代入式(5-44),变换代数式并积分后可得

考虑到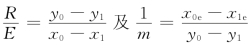,可得

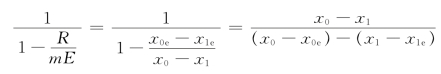
因此可得出:

式中

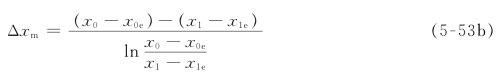
称为对数平均浓度差,也就是转盘塔进、出口传质推动力的对数平均值。

对于萃取相,同样可以得到:

式中

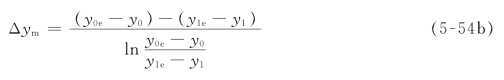
通过式(5-53)和式(5-54),还可加深对传质单元数物理意义的理解。从上述两式可以看出,NTU在数值上等于萃取塔的浓度变化量相对于对数平均浓度差的倍数。若萃取塔进出口浓度变化(x0-x1)正好等于对数平均浓度差Δxm,那么这个萃取塔正好相当于一个传质单元。这个萃取塔的高度也就是一个传质单元高度(参看图5-12)。

2)平衡线为曲线的情况

在一般情况下,平衡线为曲线,(x-xe)随萃余相浓度x变化的规律比较复杂。通常可以采用数值积分法或图解积分法求传质单元数,设计时可参阅文献[1,6]。

在两相部分互溶时,两相流量沿着塔高显著地发生变化。当料液浓度很高而萃取率也很高时,在萃取过程中,萃取相流量也有较大变化。在这些情况下,需要对传质单元数的计算方法做些修正。具体可参阅文献[3]。

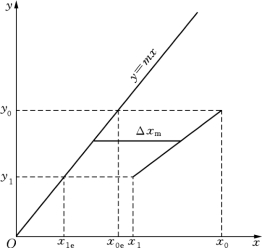
图5-12　传质单元示意图

5.3.3.3　理论级和理论级当量高度

工程上也常采用理论级和理论级当量高度的方法来估算萃取塔的高度。转盘塔的高度L可以表示为:

式中,NT为萃取过程所需的理论级数;He为理论级当量高度,即HETS,m。

理论级当量高度He的物理意义是:两相逆流流过这样高度的一段萃取塔后,其分离效果相当于一个理论级。其大小反映了萃取塔传质效率的高低。He的数值与塔结构、物系性质及操作条件有关,需经实验测定。

与精馏过程类似,完成一定分离任务所需的理论级数可以用图解法或逐级计算法求得。但是,由于连续逆流传质过程和逐级接触萃取过程有本质上的差别,因此采用理论级和理论级当量高度的方法,往往很难进行可靠的放大设计。