实验测定返混传质数据求真实总传质系数

5.3.2.1　滴内传质分系数

1)停滞液滴的传质

液滴在连续相中运动,当直径很小、速度很低时(Re=dpuSρC/μC＜10),液滴内部处于停滞状态,犹如刚性球一般,滴内的传质全靠分子扩散。这种情况的传质可以看作和其他条件作比较时的极限情况。传质分系数kD可按下式计算:

式中,kD为滴内传质分系数,m/s;DD为滴内分子扩散系数,m2/s;dp为液滴直径,m。

2)滞流内循环液滴的传质

当液滴较大时(Re＞10),液滴在连续相中运动,界面上的摩擦力会诱导出如图5-9(a)所示的滴内环流。滞流内循环液滴的传质分系数可用下式近似计算

式中符号与式(5-23)相同。

3)湍流内循环液滴的传质

湍流内循环的流型如图5-9(b)所示。当运动速度大时(有人建议Re＞80),液滴内不仅有切向作用力,还有径向作用力。后者使液滴变形产生摆动,即在圆球形与椭圆球形之间来回变化。由于液滴摆动所引起的界面拉伸和内部循环混合的联合作用,使得液滴的传质速率增高。在连续相阻力可以忽略时,滴内传质分系数可用下式计算:

式中,uS为两相相对速度,m/s;μD、μC分别为分散相、连续相的黏度。

人们已对内循环液滴提出了多种模型,但由于问题复杂,研究还有待深入。

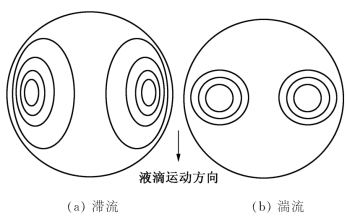
图5-9　液滴内循环的流型

5.3.2.2　滴外传质分系数

1)停滞液滴外侧的传质

对于停滞液滴,Treybal提出的计算滴外传质分系数kC的近似式为:

式中,uS为两相相对速度,m/s;kC为滴外传质分系数,m/s。

Calderbank等人建议用下式计算:

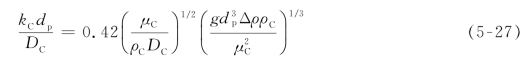
式中,DC为滴外分子扩散系数;g为重力加速度。也有人认为此式也适用于循环液滴外侧的传质。

2)内循环液滴外侧的传质(www.xing528.com)

液滴内循环可减少液滴外侧边界层的厚度,因而使传质系数增大,通常可采用下式估算内循环液滴外侧的传质分系数:

此式在计算黏度较大的液滴时误差较大,因此有人建议将上式修正为:

Calderbank和Moo-Young提出,在有搅拌的情况下滴外传质分系数可用下式计算:

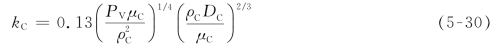
式中,PV为单位体积液体的功耗,W。

5.3.2.3　总传质系数

设萃取相(溶剂)为分散相,萃余相(料液)为连续相,溶质在两相中的平衡关系为:

式中,x为萃余相浓度,kmol/m3;y为萃取相浓度,kmol/m3;m为溶质在两相间的分配系数。

按双膜理论,总传质系数可表示成如下两式:

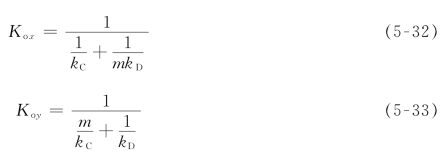
式中,Kox为以萃余相浓度差为推动力的总传质系数,m/s;Koy为以萃取相浓度差为推动力的总传质系数,m/s。

各种情况下的kD和kC可按式(5-23)～式(5-30)计算,然后根据式(5-32)或式(5-33)估算总传质系数。

当界面被少量杂质污染或存在表面活性物质时,界面扰动减弱,液滴内循环衰减甚至停止,因而使传质速率显著降低。这种现象在工程上是很重要的,设计时应予以考虑。必要时,应以实际物料进行中间试验。

关于转盘塔的传质特性研究很多,得出了许多传质系数的关联式[9]。Strand等人曾对转盘塔的传质特性进行了研究和分析,他们考虑了返混的影响后,得到了真实的总传质系数的测量值,然后与从停滞液滴和湍流内循环液滴传质分系数求出的总传质系数进行了比较。对于停滞液滴,kD用式(5-23)计算,kC用式(5-26)计算;对于内循环液滴,kD用下式计算:

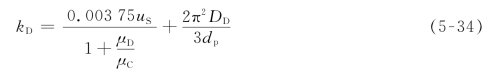
kC用式(5-28)计算。实验结果和计算结果用图5-10的方式进行比较。对于甲苯(分散相)-丙酮-水体系,当丙酮由分散相向连续相传质时,不同直径的转盘塔的实验数据处于停滞液滴和内循环液滴的计算值之间。其他的实验还表明,体系、传质方向和微量界面污物的存在都会影响实验结果。但是,塔径对结果并没有影响。因此,从小型实验塔求得的传质实验数据,按这种方式处理后,可以用来预测大型转盘塔的传质性能。

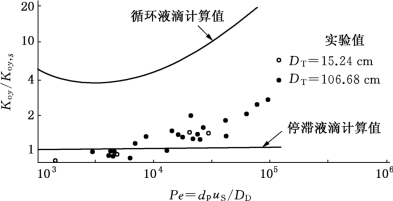
图5-10　转盘塔的传质性能——测量值与计算值之比较

苏元复等人也对转盘塔的传质性能进行了系统研究。根据实验测定的返混和传质数据,求出真实总传质系数。把此值与按停滞液滴理论模型的预测值之比Koy/Koy,s看作是液滴Peclet数(Pedr=dpuS/DD)的函数,经过回归分析,得出如下关联式:

在进行转盘塔放大设计时,只要算出给定条件下的Koy,s和Pedr,就可以从式(5-35)求出塔内真实的总传质系数(Koy)。