再沸器的优化工艺设计方案

由于立式热虹吸再沸器具有一系列的突出优点和优良性能,工业上首先考虑选用立式热虹吸再沸器。另外,立式热虹吸再沸器是依靠单相液体与气液混合物间的密度差为推动力来形成釜液流动循环的,其釜液循环流量、压力降及热流量之间相互关联。因此,在对立式热虹吸再沸器进行工艺设计时需将传热计算和流体力学计算相互关联,采用试差的方法进行计算,计算过程较复杂。这里主要介绍其工艺设计,其他型式的再沸器的工艺设计可参考文献[1,4]。

如图2-19所示,立式热虹吸再沸器内的流体流动系统是由塔釜内液位高度Ⅰ、塔釜底部至再沸器下部封头管箱的管路Ⅱ、再沸器的管程Ⅲ及其上部封头至入塔口的管路Ⅳ所构成的循环系统。工艺设计时先假设传热系数,估算传热面积,其基本步骤介绍如下。

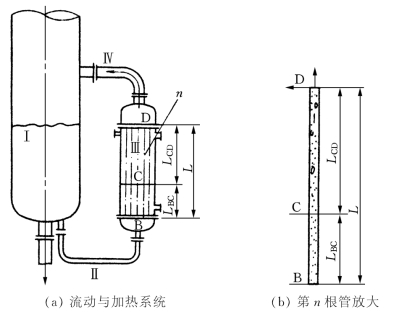
图2-19　再沸器管程的加热方式

2.5.3.1　估算再沸器尺寸

(1)再沸器的热流量

根据实际情况,再沸器的热流量可以管程液体蒸发所需的热流量或以壳程蒸汽冷凝所释放的热流量为准,按下式计算

式中,r为物流相变热,kJ/kg;D为相变质量流量,kg/s;b,c分别表示蒸发与冷凝。

(2)计算传热温度差Δtm

若已知壳程水蒸气冷凝温度为T,管程中釜液的泡点为tb,则Δtm为

若已知壳程或管程中混合蒸气露点为Td、泡点为Tb,管程或壳程中釜液的泡点为tb,则Δtm为

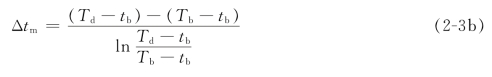
(3)假定传热系数K

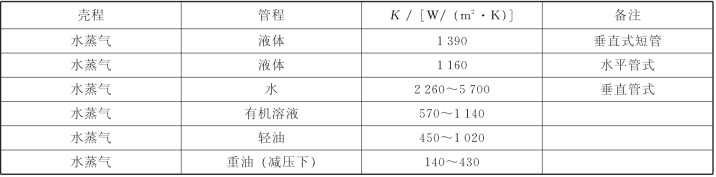
依据壳程中介质的种类,查表2-15。从中选取某一K值,作为假定的传热系数K,计算实际传热面积Ap。

表2-15　传热系数K值大致范围

(4)工艺结构设计

根据选定的单程传热管长度L及传热管规格,按下式计算总传热管数NT为

若管板上传热管正三角形排列时,则排管构成正六边形的个数a、最大正六边形内对角线上管子数目b和再沸器壳体内径D可分别按下式进行计算。

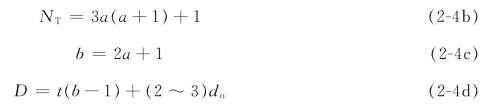
式中,NT为排列管子总数;a为正六边形的个数;t为管心距,mm;do为传热管外径,mm。

再沸器的接管尺寸可参考表2-16选取。

表2-16　再沸器接管直径

2.5.3.2　热流量核算

立式热虹吸再沸器传热管内流体被加热的方式如图2-19(b)所示,由于塔釜内存在一定的液位高度,所以当釜液流入管内B点时,流体的温度必定低于其压力所对应的泡点,当流体沿管上流,被加热至泡点(对应于点C)之前时,管内液体是单相对流传热,即管内流体在LBC段中所获得的热量仅作为其升温显热,故LBC段称为显热段,若该段的传热系数KL大一些,则LBC会短一些,流体流经C点之后直至D点,即在LCD段流体将沸腾而部分蒸发成为气、液混合物,故LCD段称为蒸发段,在此段中流体呈气、液两相混合流动。可见,每根传热管都是由显热段和蒸发段两部分组成的。

若塔釜内液面高度低于再沸器上部板下缘,则不能提供足够大的釜液循环所需要的推动力ΔpD。因为ΔpD的形成首先要靠密度差(管程C点之后的流体密度显著小于塔釜中液体的密度),其次要靠塔釜内液面高度。实际上,一般要求塔釜内液面高度与再沸器上部板处于同一水平高度上,如图2-19(a)所示。这样确定塔釜内液面高度可使显热段较短而传热系数KL较高。设计计算中还要适当选取管程的进、出口管内径Di、Do,以保证较小的汽化率,最终使再沸器满足工艺的热流量。

如上所述,立式热虹吸式再沸器的热流量核算,应分别计算显热段和蒸发段各自的传热系数,然后取其平均值(按管长平均)作为其总传热系数。

(1)显热段传热系数KL

显热段传热系数的计算方法与无相变换热器的计算方法相同,但为求取传热管内的流体流量,需先假设传热管的出口汽化率,然后在流体循环量核算时核算该值。

①釜液循环量。假设出口汽化率为xe,其值的大致范围为:对于水的汽化一般在2%～5%,对于有机溶剂一般为10%～20%。则釜液循环量为

式中,Db为釜液蒸发质量流量,kg/s;Wt为釜液循环质量流量,kg/s。

②显热段传热管内表面传热系数αi。传热管内釜液的质量流速G为

式中,so为管内流通截面积,so= NT,m2;di为传热管内径,m;NT为传热管数。

管内雷诺数Re及普朗特数Pr分别为

式中,μb为管内液体黏度,Pa·s;cpb为管内液体定压比热容,kJ/(kg·K);λb为管内液体导热系数,W/(m·K)。

若Re＞104,0.6＜Pr＜160,显热段管长与管内径之比LBC/di＞50时,按圆形直管强制湍流公式来计算显热段传热管内表面的传热系数ai。

③壳程蒸汽冷凝表面传热系数ao。壳程蒸汽冷凝的质量流量m可用下式计算:

式中,m为蒸汽冷凝液的质量流量,kg/s;Q为冷凝热流量,W;rc为蒸汽冷凝热,kJ/kg。

求得该值后,可由垂直管外冷凝给热系数的计算公式来计算壳程冷凝表面的传热系数ao。

显热段传热系数KL由此可方便地求出。

(2)蒸发段传热系数KE

要计算垂直管内气、液两相并流向上流动沸腾表面的传热系数,必须首先了解气、液两相流动沸腾传热的流动流型。如图2-20所示,沸腾开始时,首先是鼓泡流,当气泡相连而变大时,就成为块状流。再往上,管中心就成为连续的汽心,称为环状流。从块状流到环状流的过渡区一般都不稳定。据有关资料介绍,当汽化率xe达到50%以上,就基本上成为稳定的环状流。当汽化率xe增加到一定程度,就进入雾状区。在该区域内,壁面上的液体全部汽化,只有汽心中有些液滴。这时,不仅表面传热系数下降,而且壁温剧增,易于结垢或使物料变质。

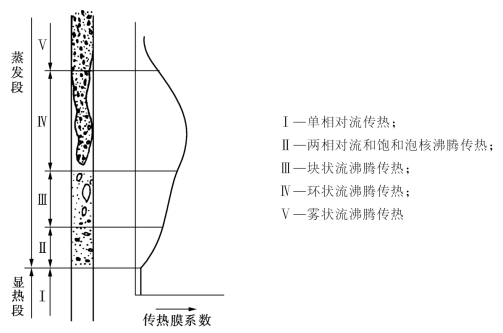
图2-20　管内沸腾传热的流动流型及其表面传热系数

在再沸器的设计中,为了使其在操作时具有稳定性,应将汽化率xe之值控制在25%以内。因此,沸腾传热的流动流型是处在饱和泡核沸腾和两相对流传热的流动流型中。目前一般采用双机理模型来解决管内沸腾传热问题。所谓双机理模型就是同时考虑两相对流传流机理和饱和泡核沸腾传热机理,可采用以下经验关联式来计算管内沸腾表面传热系数。

式中,αv为管内沸腾表面传热系数,W/(m2·K);αtp为两相对流表面传热系数,W/(m2·K);αnb为泡核沸腾表面传热系数,W/(m2·K);a为泡核沸腾压抑因数,量纲一。

①两相对流给热膜系数αtp按下式计算

式中Ftp称为对流沸腾因子,是Xtt[马蒂内利(Martinelli)参数]的函数。不少研究者都提出以下函数式

若令

φ=(ρv/ρb)0.5(μb/μv)0.1

则

式中,x为蒸气的质量分数,即汽化率;ρv、ρb分别为沸腾侧气相与液相的密度,kg/m3;μv、μb分别为沸腾侧气相与液相的黏度,Pa·s。

对流沸腾因子的具体公式列于表2-17中,可见,不同研究者所得结果有所不同。

表2-17　对流沸腾因子

在再沸器的设计中采用了登格勒(Dengler)及亚当斯(Addams)关联式来计算Ftpo

由于蒸发段的汽化率是不断变化的,因此,设计上一般取汽化率为出口汽化率的40%处的值作为平均值,即令x=0.4xe,用式(2-13)求得Xtt,再用式(2-14)求得Ftp。

αi是以液体单独存在为基础而求得的管程表面传热系数(www.xing528.com)

用式(2-10)可求得两相对流表面传热数αtp。

②泡核沸腾表面传热系数αnb。已发表的计算泡核沸腾表面传热系数的公式颇多,在两相流沸腾给热中,许多研究者推荐应用麦克内利(Mcnelly)公式

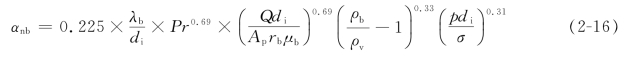
式中,di为传热管内径,m;rb为釜液汽化潜热,kJ/kg;p为塔底操作压力(绝对压),Pa;σ为釜液表面张力,N/m。

③泡核沸腾压抑因数a。该值也与汽化率有关,一般按下式取平均值

式中,aE为传热管出口处泡核沸腾修正系数,量纲一;a′为对应于汽化率等于出口汽化率40%的泡核沸腾修正系数。

这两个修正系数都与管内流体的质量流速Gh[kg/(m2·h)]及1/Xtt(相关参数)有关。

式中,G为传热管内釜液的质量流速,kg/(m2·s);Gh为传热管内釜液的质量流速,kg/(m2·h)。

若令x等于传热管出处的汽化率xe,则可先用式(2-13)求得此时的1/Xtt,而后再用式(2-18)求得此时的Gh,由垂直管内流型图(图2-21)可查得aE;若令x=0.4xe,则可重复上述过程,得到的值是a′。用式(2-17)可求得泡核沸腾压抑因数a,于是可用式(2-9)求得管内沸腾表面传热系数αv。

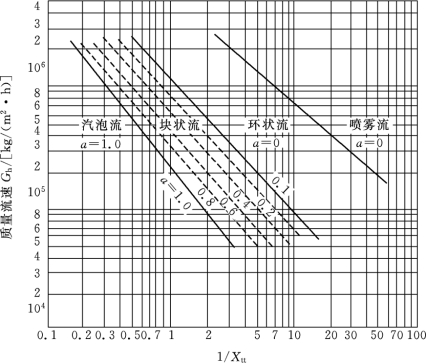
图2-21　垂直管内流型图

求得以上各量后即可计算蒸发段传热系数KE。

(3)显热段和蒸发段的长度

显热段的长度LBC与传热管总长L的比值为

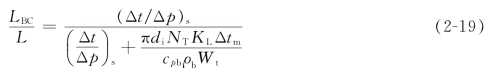
式中(Δt/Δp)s为沸腾物系的蒸气压曲线的斜率,常用物质的蒸气压曲线的斜率可由表2-18查取,或根据饱和蒸气压与温度的关系来计算。

表2-18　常用物质蒸气压曲线的斜率

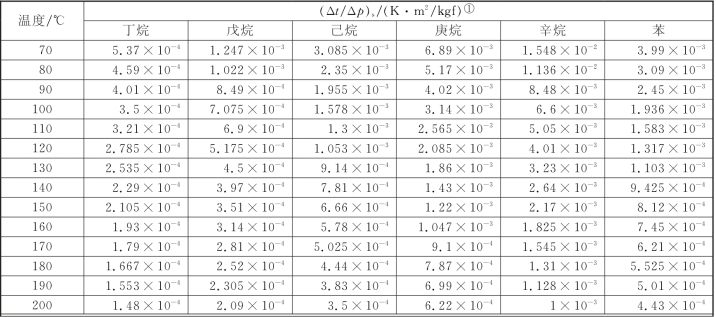
①注:1 kgf=9.8N

续表

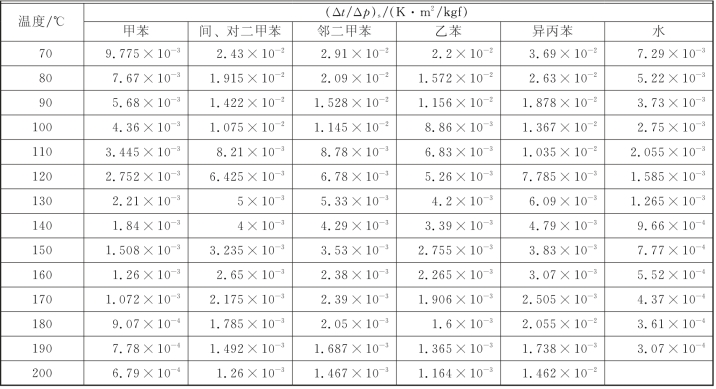
根据式(2-19)可求得显热段和蒸发段的长度LBC与LCD。

(4)计算传热系数KC

(5)面积裕度核算

求得传热系数后,可计算需要的传热面积和面积裕度。由于再沸器的热流量变化相对较大(因精馏塔常需要调节回流比),故再沸器的裕度应大些为宜,一般可在30%左右。若所得裕度过小,则要从假定K值开始,重复以上各有关计算步骤,直到满足上述条件为止。

2.5.3.3　循环流量的校核

由于在传热计算中,再沸器内的釜液循环量是在假设的出口汽化率下得出的,因而釜液循环量是否正确,需要核算。核算的方法是在给定的出口汽化率下,计算再沸器内的流体流动循环推动力及其流动阻力,应使循环推动力等于或略大于流动阻力,则表明假设的出口汽化率正确,否则应重新假设出口汽化率,重新进行计算。

(1)循环推动力

如图2-19所示,釜液循环推动力ΔpD是由于釜液在管内从C点开始汽化形成两相混合物,其密度小于塔釜液体的密度,由此而产生密度差,形成了循环推动力。在再沸器内,与釜液具有密度差的流体柱高度为蒸发段LCD,因此,ΔpD为

式中,ΔpD为循环推动力,Pa;LCD为蒸发段高度,即相应的塔釜液柱高度,m;ρb为釜液密度,kg/m3;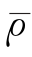tp为蒸发段的两相流的平均密度,kg/m3;ρtp为管程出口管内的两相流密度,kg/m3;l为再沸器上部管板至接管入塔口间的高度,m。

其中的l值可参照表2-19,结合再沸器公称直径进行选取。

表2-19　l的参考值

其他各参数按如下方式处理。

式中,RL为两相流的液相分率,其值为

蒸发段的两相流平均密度以出口汽化率的计算,即取x=,由式(2-21)求得的Xtt代入式(2-23),从而求得RL,再应用式(2-22)可求得ρtp;管程出口的两相流密度为常数,取x=xe,按上述同样的步骤可求得ρtp。

(2)循环阻力

如图2-19所示,再沸器中液体循环阻力Δpf(Pa)包括管程进口管阻力Δp1、传热管显热段阻力Δp2、传热管蒸发段阻力Δp3、因动量变化引起的阻力Δp4和管程出口管阻力Δp5,即

①管程进、出口管阻力Δp1。管程进、出口管阻力按下式计算:

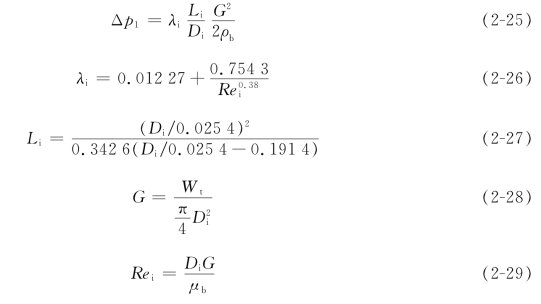
式中,λi为摩擦系数;Li为进口管长度与局部阻力当量长度之和,m;Di为进口管内径,m;G为釜液在进口管内的质量流速,kg/(m2·s)。

②传热管显热段阻力式中Δp2。传热管显热段阻力式中Δp2可按直管阻力计算:

式中,λ为摩擦系数;LBC为显热段长度,m;di为传热管内径,m;G为釜液在传热管内的质量流速,kg/(m2·s)。

③传热管蒸发段阻力Δp3。该段为两相流,故其流动阻力计算按两相流考虑。计算方法是分别计算该段的气、液两相流动阻力,然后按一定方式相加,以求得阻力。

气相流动阻力Δpv3为

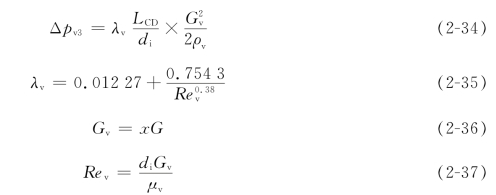
式中,λv为气相摩擦系数;LCD为蒸发段长度,m;Gv为气相质量流速,kg/(m2·s);Rev为气相流动雷诺数;x为该段的平均汽化率。

式(2-36)中的x可以取x=2xe/3进行计算,G为釜液在传热管内的质量流速,单位为kg/(m2·s),其值可按式(2-32)计算。

液相流动阻力ΔpL3为

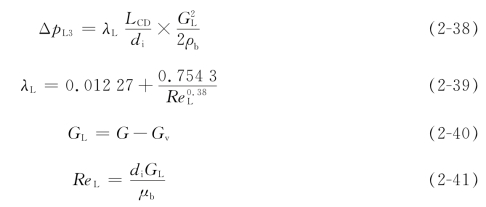
式中,λL为液相摩擦系数;GL为管程出口管液相质量流速,kg/(m2·s);ReL为液相流动雷诺数。

将以上两相阻力加和,得两相流动阻力Δp3为

④管程内因动量变化引起的阻力Δp4。由于在传热管内沿蒸发段汽化率渐增,两相流动加速,故管程内因动量变化所引起的阻力Δp4为

式中,G为管程内流体的质量流速,kg/(m2·s);M为动量变化引起的阻力系数,其值可按式(2-44)计算。

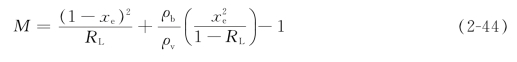
⑤管程出口管阻力Δp5。该段也为两相流,故其流动阻力计算方法与传热管蒸发段阻力Δp3的计算方法相同,但需注意,计算中所用管长取再沸器管程出口管长度与局部阻力当量长度之和,管径取出口管内径,汽化率取传热管出口汽化率。

根据以上计算,若循环推动力ΔpD与循环阻力Δpf的比值在1.001～1.05之间,则表明所设计的再沸器所假设的传热管出口汽化率xe正确,否则,重新假设传热系数K及汽化率xe,重复上述的全部计算过程,直到满足传热及流体力学要求为止。

因篇幅所限,其他型式的再沸器工艺设计及设计示例可参考文献[1,4]。