图7-7所示为12个和32个型腔的流道系统。图中三种布局都为非自然平衡,从主流道至各注射点的流径长度不同。显然,离主流道远的注射点的熔体充模压力较低,所注射制品的保压不足,成型后制品的密度较低,收缩率较大,会使各型腔成型制品的质量与尺寸不一致,降低产品的精度。因此,必须经流变学计算,调节截面尺寸,使所有注射点的注射压力一致。但计算实现流变学平衡较为困难。图7-7b和c布排的第一层次的分流道实现了自然平衡,但第二层次是非自然平衡,所以是一种混合型的流道系统。在此系统中,实现第二层次的流变学平衡较为容易。
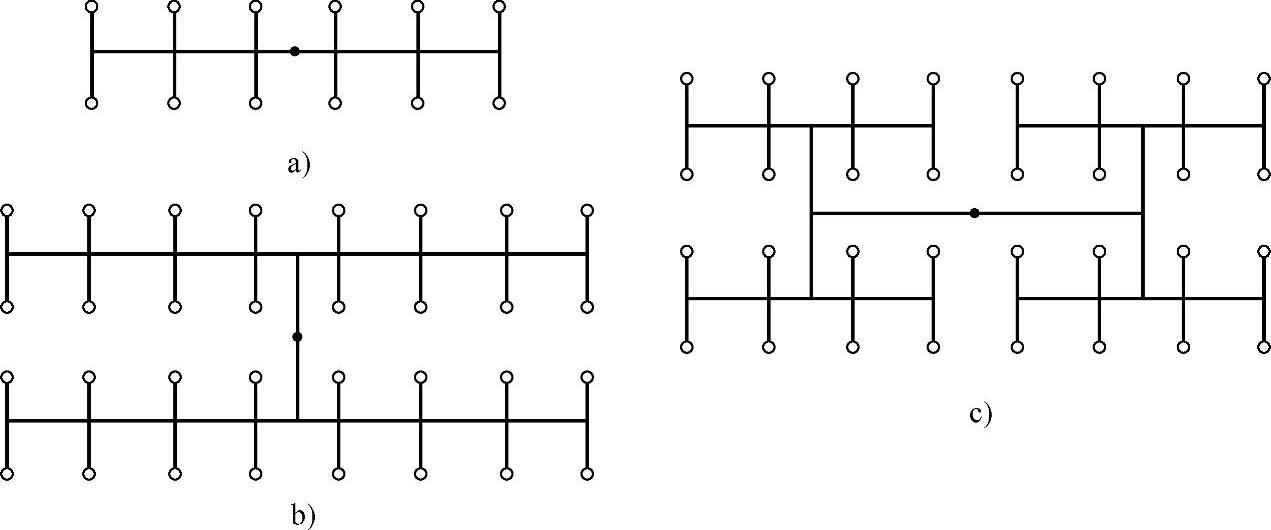
图7-7 12和32个型腔的流道系统
a)非平衡的流道系统 b)、c)部分自然平衡的流道系统
通过调节喷嘴温度,改变熔体的黏度,实现各注射点的压力一致,是不可取的,这会使各型腔的温度不同,结果是各型腔制品的残余应力和收缩率不一致。
实现理想的充模平衡是不容易的,这是因为流变学的平衡计算存在误差,热流道系统的机械加工有误差,而且生产中的工艺参量也是变数,如不均匀的排气就会影响熔体充填型腔的平衡。
人工计算或者计算机流动模拟的流变学平衡与自然平衡的流道系统相比较,流道的长度较短,流道的总体积较小,因此流道板较简单,体积小,重量轻。
对于一模多腔的流变学平衡浇注,也可以用计算机模拟方法进行,但需对流道系统和注塑件进行计算机造型,然后多次修改流道直径,直到屏幕显示各注射点有相同的压力降。由于造型和修改操作费时,因此花费的设计工时反而比人工或编程计算要多。
但是,在流变学平衡设计计算流道时,计算结果是在一定工艺条件的温度和流动速率下获得的。在实际注射生产时,使用的塑料品种牌号和工艺参量与计算预测不一致时,就会有黏度的误差,以致偏离平衡,况且流变学平衡设计计算需专业的技术和技能,必须有塑料流变参量的数据。
1.流道的流变平衡设计
(1)8型腔单层直排流道的流变学平衡设计 对于一模多腔流道系统的流变学平衡,可以人工完成设计计算。图7-10所示为一模八腔的流变学平衡计算的结果。从主流道始,至每个注射点的熔体在流道中的压力降都是5.2MPa。它通过改变流道的截面,将短流径的流道直径减小,又将长流径的流道直径增大,获得压力状态的平衡。
下面是对于共聚甲醛POM,注射熔体温度为200℃,注射充模时间为0.7s,各个型腔体积V型为3cm3的计算。
图7-8a所示的流道系统的一半被分解成四个流程,每个流程又分成若干个计算段。从计算O点起,D流程仅有一段,B流程有三段,A流程是等直径d1的三段。不计流道中熔体的体积,通过A流程1段的熔体体积为3/8V型,通过A流程2段的体积为2/8V型,流过A流程3段的体积1/8V型。
1)计算注入流道系统的体积流率。
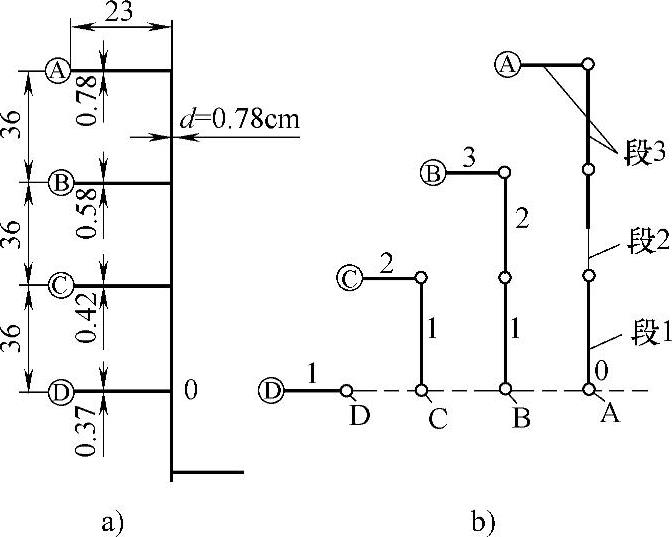
图7-8 8个型腔的流道的流变平衡设计图解
a)型腔分布和流道直径计算结果 b)流程的计算分段
每次注射塑料熔体体积V=8V型=8×3cm3=24cm3。查表5-3,注射充模时间t=0.7s。
见图7-8,A流程3段、B流程3段、C流程2段和D流程1段的体积流率

由此类推,A流程2段和B流程2段的体积流率q2=8.6cm3/s,A流程1段、B流程1段和C流程1段的体积流率q1=12.8cm3/s。
2)计算A流程的三段分流道直径d1。由式(3-7),有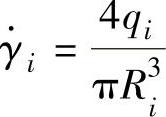 。假设R1=0.80cm/2=0.40cm,计算第三段分流道,在q1=12.8cm3/s、q2=8.6cm3/s和q3=4.3cm3/s时剪切速率
。假设R1=0.80cm/2=0.40cm,计算第三段分流道,在q1=12.8cm3/s、q2=8.6cm3/s和q3=4.3cm3/s时剪切速率
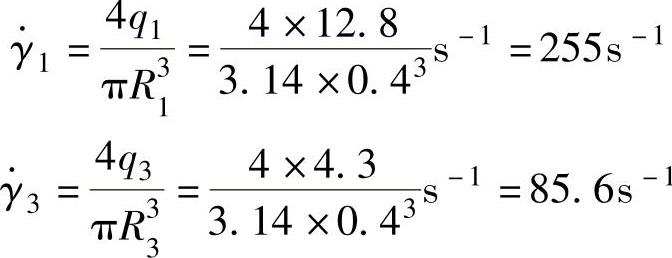
当R1=0.40cm,q3=4.3cm3/s时A流程3段流道中剪切速率
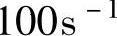 ,流道中输送熔体的黏度过稠。经几次试算,确定A流程三段分流道直径d1=0.78cm,A流程1段、A流程2段和A流程3段流道中剪切速率分别为
,流道中输送熔体的黏度过稠。经几次试算,确定A流程三段分流道直径d1=0.78cm,A流程1段、A流程2段和A流程3段流道中剪切速率分别为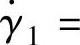
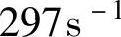 、
、 和
和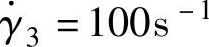 ,见表7-5。
,见表7-5。
3)计算A流程的三段流道总压力损失。
POM表观黏度ηa与剪切速率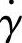 的流变曲线如图7-9所示。在熔体温度200℃曲线上,由剪切速率
的流变曲线如图7-9所示。在熔体温度200℃曲线上,由剪切速率 查得表观黏度ηa。当A流程1段流道的剪切速率
查得表观黏度ηa。当A流程1段流道的剪切速率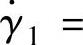
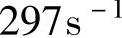 ,表观黏度ηa=370Pa·s。由此得A流程1段的压力降:
,表观黏度ηa=370Pa·s。由此得A流程1段的压力降:
表7-5 一模八腔热流道的流变计算
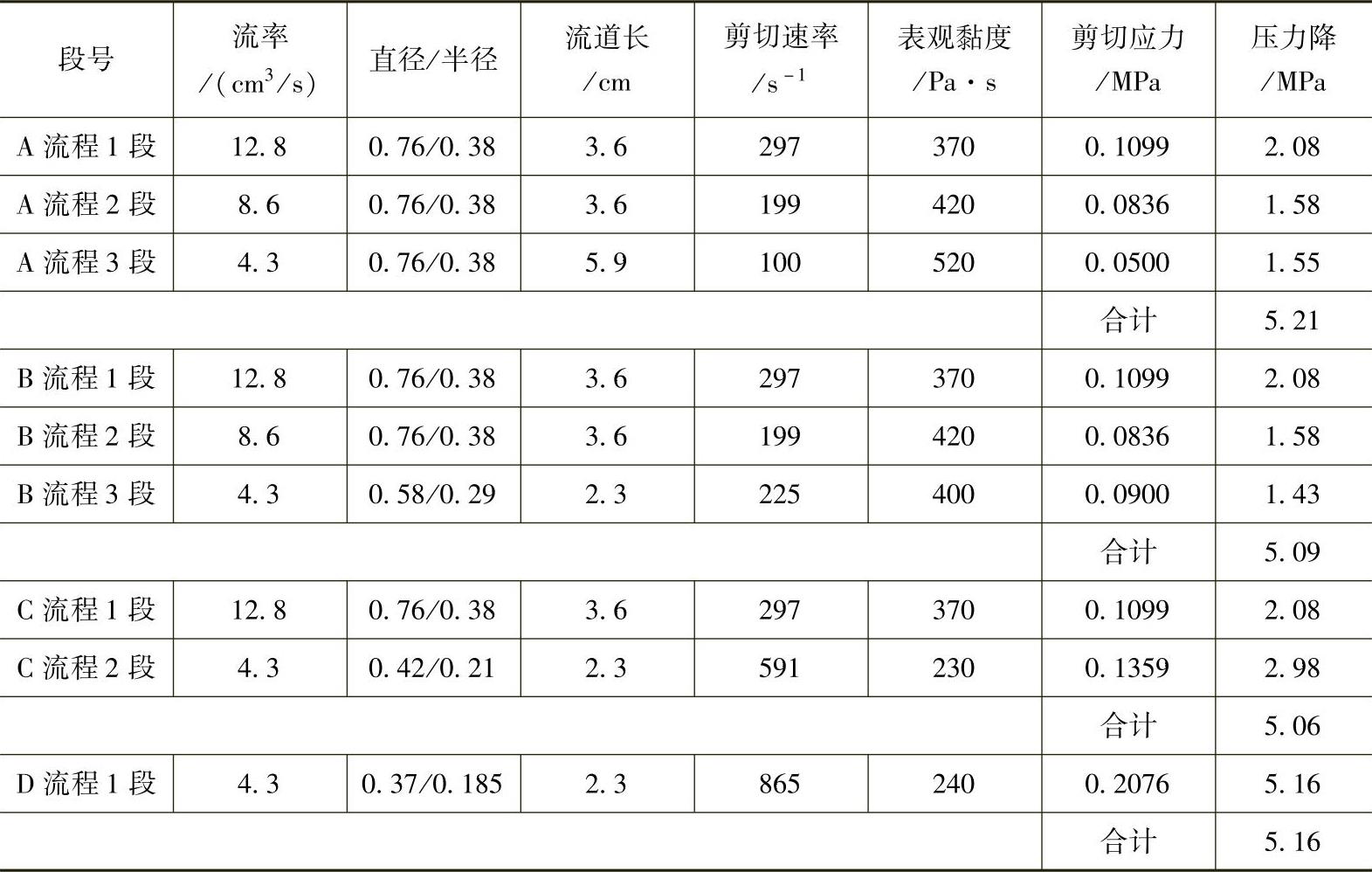

有
同样可以预测A流程2段和A流程3段流道中的压力降分别为1.58MPa和1.55MPa,见表7-5。A流程总共有(2.08+1.58+1.55)MPa=5.21MPa压力降。
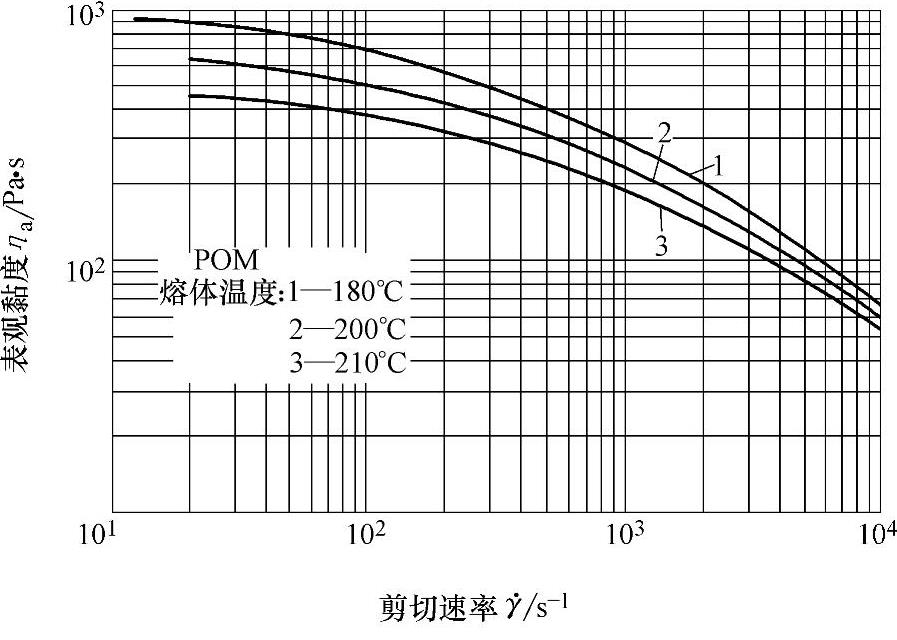
图7-9 POM表观黏度ηa与剪切速率 的流变曲线
的流变曲线
4)试算B流程3段、C流程2段和D流程1段流道直径,直到B、C与D三流程的压力损失等于A流程的压力降。
B流程中B流程1段和B流程2段与A流程1段和A流程2段的长度一致,均为3.6cm。为实现流变平衡,B流程3段与A流程3段应有相同的压力降,也就是B流程3段的2.3cm长有较细的直径,与A流程3段(2.3+3.6)cm=5.9cm长、直径0.78cm有相近的1.43~1.55MPa压降。经计算得B流程3段直径为0.58cm时,可实现平衡浇注,详见表7-5和图7-8。
对于本实例8个型腔单层直排流道的流变平衡设计,有以下三条说明:
①较高的熔体温度和较短的充模时间都能改善塑料熔体的流动性,有利于充模压力的传递。计算过程时,应取适中的充模时间和熔融温度。在注射生产时,对照流变平衡计算中设定的温度与时间要有调节余地。
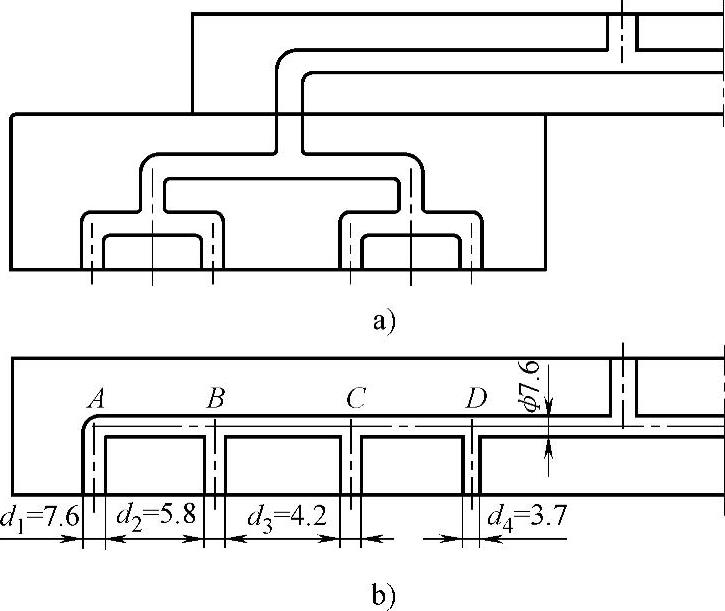
图7-10 一模八腔的两种热流道
a)三层次的自然平衡流道板 b)流变学平衡的流道板
②如图7-10所示,一模八腔的直排的流变平衡的流道板是单层的,与几何平衡布置的流道板相比,流道长度短了,流道板高度压缩了一半。
③在本例流变学平衡计算中,塑料熔体的流变性能数据回避了稠度K和流动指数n,不使用剪切速率 与表观黏度ηa流变曲线,依赖于剪切速率
与表观黏度ηa流变曲线,依赖于剪切速率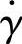 与剪切应力τ流变曲线。这不同于本书着重介绍的流变学平衡计算的途径,但两者的计算原理和方法是相同的。目前,各种塑料熔体的剪切速率
与剪切应力τ流变曲线。这不同于本书着重介绍的流变学平衡计算的途径,但两者的计算原理和方法是相同的。目前,各种塑料熔体的剪切速率 与剪切应力τ流变曲线很难获得,因此流变平衡计算还是用参数K和n及
与剪切应力τ流变曲线很难获得,因此流变平衡计算还是用参数K和n及 流变曲线为好。从
流变曲线为好。从 流变曲线获得K和n参数的方法在第3章中有详细介绍。
流变曲线获得K和n参数的方法在第3章中有详细介绍。
(2)16型腔的流变学平衡流道设计 高22mm、外径为35mm的HDPE盖帽,壁厚为1.73mm,重量Gi=4.6g。16件盖帽塑件两行直排,以2×2×4分叉布局流道。已确定用16个导流梭针尖喷嘴,喷嘴流道直径为5mm,针尖浇口直径为1.0mm。流变学设计的流道布局和直径计算结果就是如图7-11所示的16型腔的流道的流变平衡设计。与图7-6所示的16型腔布局相比,其流道板的最大特点是单层整块,刚度好,高度低。
1)计算注入流道系统的体积流率。
查表2-7,HDPE塑料熔体的密度ρm=0.727g/cm3。
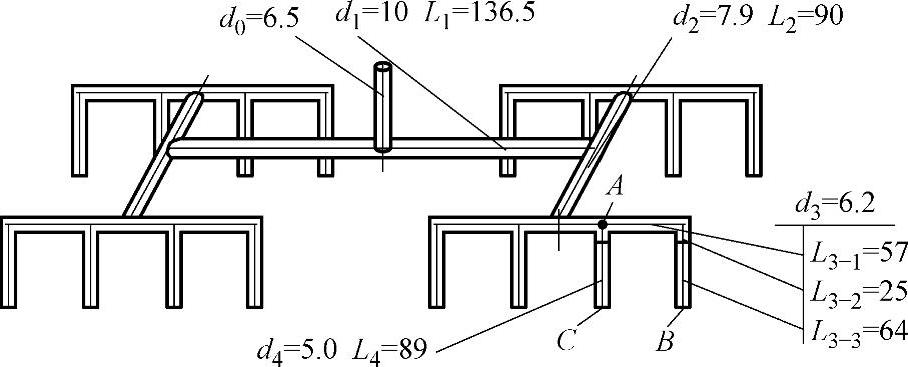
图7-11 16个型腔的流道的流变平衡设计
每个制件的熔体体积Vi=Gi/ρm=(4.6/0.727)cm3=6.33cm3。
每次注射塑料熔体体积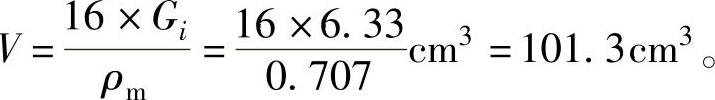
查表5-3,注射充模时间t=1.38s。
主流道喷嘴的体积流率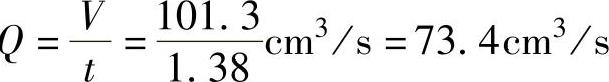
第1、2和3分流道的体积流率分别为q1=36.7cm3/s、q2=18.35cm3/s和q3=9.18cm3/s。
2)确定自然平衡流道的直径。
查表3-2,230.7℃时,流动速率MFR=9.8g/10min的HDPE塑料熔体在剪切速率 时,稠度K′=K=4663Pa·s=0.4663N·s/cm2,流动指数n=0.434。
时,稠度K′=K=4663Pa·s=0.4663N·s/cm2,流动指数n=0.434。
将分流道合理的剪切速率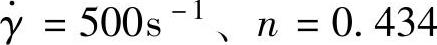 及q1=36.7cm3/s代入式(3-21),得第1分流道直径
及q1=36.7cm3/s代入式(3-21),得第1分流道直径

将q2=18.35cm3/s代入式(3-21),其他参数同上,得第2分流道直径
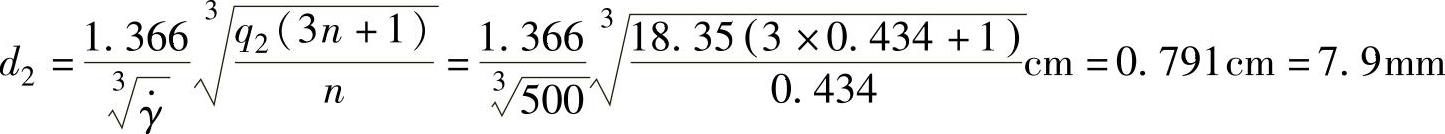
用式(7-1)计算一分为二的分叉流道的分流道直径,得

计算结果与式(3-21)相同。同理,得第3分流道直径
 。
。
查表3-2,流动速率MFR=9g/10min的HDPE塑料熔体在剪切速率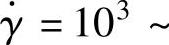
 时,稠度K′=K=9750Pa·s=0.9750N·s/cm2,流动指数n=0.327。
时,稠度K′=K=9750Pa·s=0.9750N·s/cm2,流动指数n=0.327。
将合理的剪切速率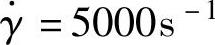 和n=0.327代入式(3-21),得主流道喷嘴的直径
和n=0.327代入式(3-21),得主流道喷嘴的直径
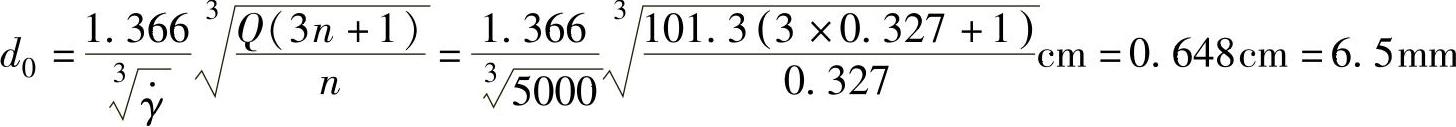
3)设计计算非平衡流道的直径。
流变平衡计算是调整AB和AC流程的流道的直径,使熔体输送流程压力损失相等,让B和C两点的注塑压力相等,如图7-11所示。AC流程在流道板上的流道长度仅25mm,采用流变平衡计算调整流道的直径不现实,故将喷嘴流道长度64mm的压力降计入调整范围。非标准的喷嘴流道直径可以加工。先将AB流程的流道直径和喷嘴内径确定为d3=6.2mm,压力损失为4.35MPa。将AC流程(直径d4)的长度计入喷嘴流道后,L4=89mm。将AC流程的流道直径和喷嘴直径d4逐次调整,当压力降等于4.34MPa时,喷嘴直径d4=5mm可实现流变平衡。一模十六腔热流道的流变平衡计算见表7-6。
表7-6 一模十六腔热流道的流变平衡计算

注:1.230.7℃时,MFR=9.8g/10minHDPE, ,K′=4663Pa·s,n=0.434。
,K′=4663Pa·s,n=0.434。
2.如图7-11所示,AB1=L3-1=5.7cm,AB2=L3-2+L3-3=8.9cm。
对于本实例16型腔单层直排流道的流变平衡设计,有以下四条说明:
①本实例2×2×4的最后一级是非平衡的流道布局。如图7-11所示,前2×2级是平衡布置,其流道设计计算必须使熔体输送具有5×102s-1左右的剪切速率,这样才能给下游的非平衡流道的流变平衡提供流道直径调整的余地。
②流变平衡是通过流道直径调整,实现AB和AC流程的压力损失相等。另外,被调整流道中仍要有100~1000s-1的剪切速率。输送熔体的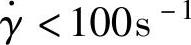 是不允许的,非牛顿流体黏度太高,会使流动阻力过大。
是不允许的,非牛顿流体黏度太高,会使流动阻力过大。
③本例流变平衡计算的AC流程在流道板上长度仅25mm,实现与AB流程的压力平衡不现实,为此将下游喷嘴流道加入,与流道板流道直径一起调整。AB和AC流程中包含了两个长65mm的喷嘴流道,因此也可确保喷嘴流道中的熔体平稳输送。如果是针阀式喷嘴,也可以与分流道串接在一起实现流变平衡,但调整针阀式喷嘴的环隙流道比较困难。
④如图7-12所示,一模十六腔直排的流变平衡的流道板是单块一层的。与图7-6所示的16型腔几何自然平衡布置的流道板相比,流道长度短了,流道板高度压缩了一半,节省了流道板所用钢材,装配方便,且减少了散热面积,还可降低加热器的功率。
2.几何关系的流道设计
非平衡布置时流道的总长度较短,但是浇口射出的熔料压力不同,影响成型制品的质量。可以通过各流道,甚至浇口尺寸的调整,实现浇注系统各输出点的压力相等。浇注系统的平衡处理在注射模的设计和热流道的流道系统的设计中具有实用意义。非平衡布置的流道尺寸计算的原理和步骤与平衡布置基本相同,其区别和难度在于流道直径和长度的函数关系拟定。
(1)几何关系的流道尺寸计算 非平衡布置流道系统的流量平衡方程和几何关系的流道尺寸计算适用于牛顿流体管道输送。它可以作为塑料熔体非平衡布置流道系统的初步试算。
1)非平衡布置流道系统的流量平衡方程。
如图7-13所示的分流道非平衡布置系统为使牛顿流体在分流道输送中就达到稳定流动,流体应同时到达各分流道末端。

图7-12 单一块的16型腔2×2×4流道板结构
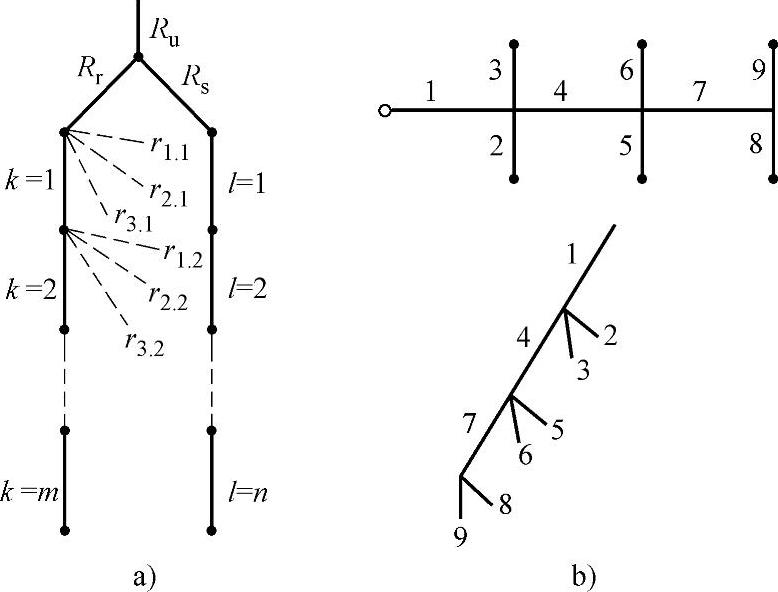
图7-13 分流道非平衡布置线图
a)流道系统非平衡布置线图 b)一模六腔非平衡布置流道(https://www.xing528.com)
如图7-13a所示,两个任意分支分流道半径Rr和Rs具有公共上游半径Ru,Rr和Rs又分别为下游各分支的半径。其中,Rr流道以下有m级支流道,Rs流道以下又有n级支流道。熔体能同时到达这两条路径末端,两支叉的熔体流动的压力降应相等,有
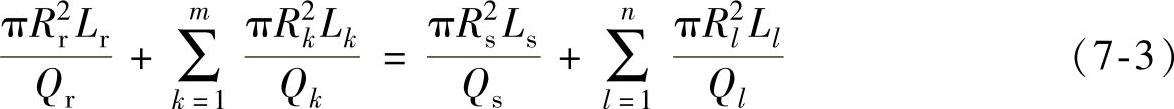
式中 m、n——分别为Rr和Rs再分支的流道数;
Rr、Qr、Lr和Rs、Qs、Ls——分别为两分支流道的半径、流量和长度;
Rk、Qk、Lk和Rl、Ql、Ll——分别为两分支的再分支流道的半径、流量和长度,k=1,2,…,m,l=1,2,…,n。
根据熔体在分流道中剪切速率相同的原则,有
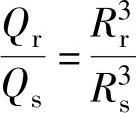
代入式(7-3),化简后得两流道间的半径比,即
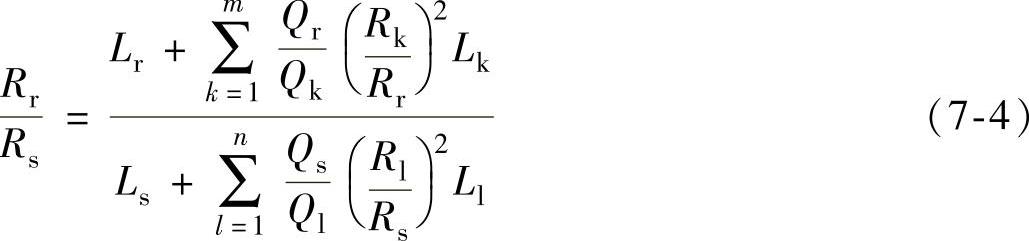
同理,在熔体流动前沿更新时,各分支流通道内的剪切速率仍应相等。若令u、d分别表示上游和下游分流道的序号,则有下面的关系式

式中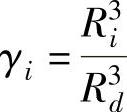 ,i=1,2,…,d-1。
,i=1,2,…,d-1。
若将 用下游分支流道半径比表示,有
用下游分支流道半径比表示,有

将式(7-5b)与式(7-5a)相乘,有

将(7-5c)代入式(7-4),可得到非平衡布置流道几何关系的比例式:
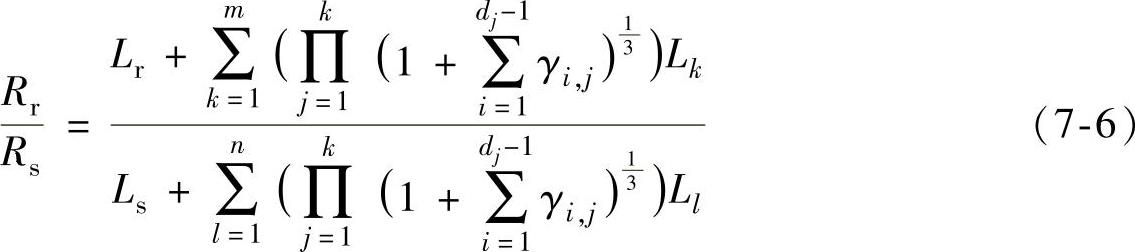
此式中j是对于r和s两支路上的节点编号,含义同k或l。因此dj是对于第“j”节点下游的分流道数目,即

显然,Lk与Ll应为与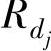 对应的长度。
对应的长度。
2)流道直径和长度的函数关系拟定。式(7-4)~式(7-6)在分流道各段长度已知时,可限定分流道的总体积,计算各分流道半径。也可根据型腔充模需要,先假定某分流道的半径,再计算其他分流道半径和流道体积。但是,此方程式与塑料的流变性质无关。计算结果必须与注射工艺和注射机技术参数结合,进行充模速率和压力降的多次校核修改。
[例] 一模六腔的流道布置如图7-13b所示。主分流道长度L1=L4=L7=2cm,支分流道长L2=L3=L5=L6=L8=L9=1cm。根据型腔充模需要,R5=R6=0.25cm。求分流道半径及流道系统总体积。
[解] 根据已知条件,在下游无支流时可由式(7-6)计算,得
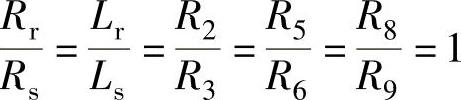
而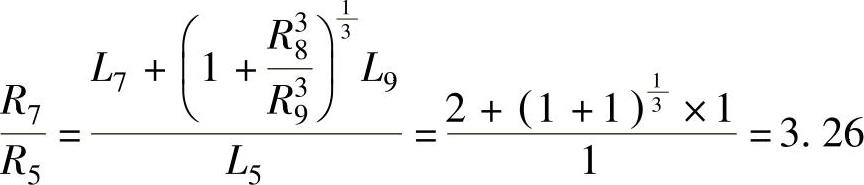

由上、下游流道半径关系式 ,有
,有
R73=R38+R39=2R38,得R7=1.26R8;
R43=R53+R36+R73=(1+1+3.263)R53=36.65R53,得R4=3.32R5;
R31=R23+R33+R43=(1+1+5.323)R23=152.57R32,得R1=5.34R2。
将R5=R6=0.25cm代入上述半径比,可得

流道总体积 。
。
此例中,R5=R6=0.25cm的确定无根据。最粗岔道R8=R9=0.647cm,是最细岔道R2=R3=0.156cm的4.47倍。最粗流道R1=0.833cm,是最细流道R2=0.156cm的4.34倍。明显不符合流道系统的分流道直径之间的比例关系。流道系统的各级流道中的剪切速率和剪切应力差异很大,塑料熔体输送流动不稳定,各注射输出点的压力不相等。
(2)几何关系的流变平衡流道计算 现有非平衡布置的一模六腔,如图7-14所示。图中注射点间距离L1=6cm,L2=L3=L5=L6=L8=L9=8cm,L4=2cm,L7=8cm。每个PC制件的重量为10g。
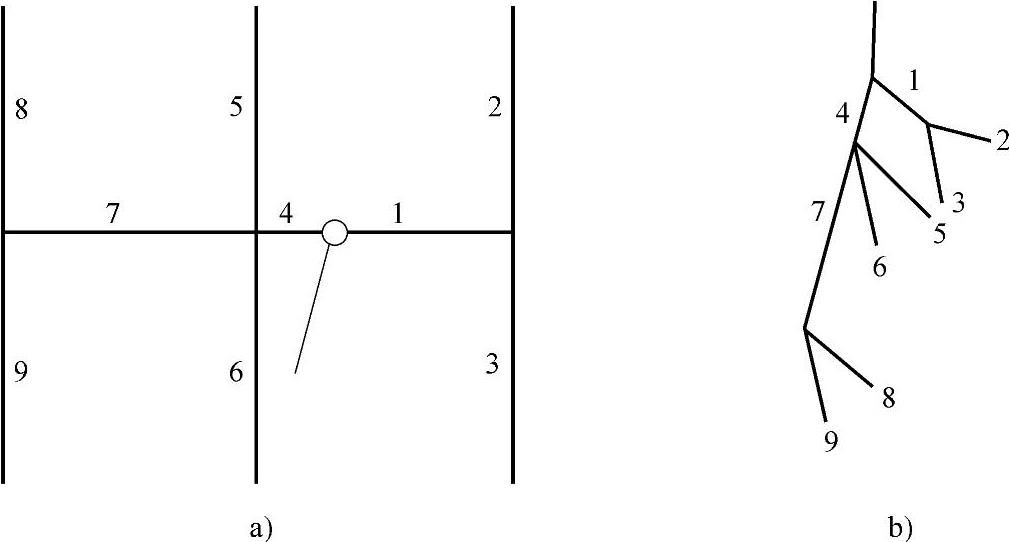
图7-14 型腔体积10cm3的一模六腔非平衡布置线图
a)流道布置 b)布置线图
1)以流体同时到达各分流道末端,做流道尺寸的初步拟定。
①由式(7-6),作图7-14b所示的布置线图,列出如下计算各流道直径的比例关系:

②计算注入流道系统的体积流率。
查表2-7,PC塑料熔体的密度ρm=1.0332g/cm3。
每个制件的熔体体积Vi=Gi/ρm=10/1.033=9.68cm3。
每次注射塑料熔体体积V=6Vi=6×9.68cm3=58.1cm3。
查表5-3,螺杆推进注射充模时间t=0.99s。
主流道喷嘴的体积流率
流道板注入喷嘴的体积流率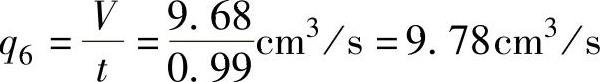 。
。
第1、第4和第7分流道的体积流率分别为q1=19.56cm3/s、q4=39.12cm3/s和q7=19.56cm3/s。
查表3-2,在260~320℃时,流动速率MFR=13g/10min的PC塑料熔体在剪切速率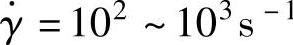 时,稠度K′=K=1947Pa·s=0.1947N·s/cm2,流动指数n=0.737。
时,稠度K′=K=1947Pa·s=0.1947N·s/cm2,流动指数n=0.737。
将分流道合理的剪切速率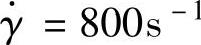 、n=0.737及q6=9.78cm3/s代入式(3-21),得第5和第6分流道直径
、n=0.737及q6=9.78cm3/s代入式(3-21),得第5和第6分流道直径

查表3-2,流动速率MFR=13g/10min的PC塑料熔体在剪切速率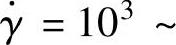
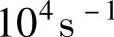 时,稠度K′=K=10931Pa·s=1.0931N·s/cm2,流动指数n=0.487。
时,稠度K′=K=10931Pa·s=1.0931N·s/cm2,流动指数n=0.487。
将合理的剪切速率 和n=0.487代入式(3-21),得主流道喷嘴的直径
和n=0.487代入式(3-21),得主流道喷嘴的直径

以第5和第6分流道直径d6=5mm,按上述计算各流道比例关系得到表7-7初定的各段流道半径和长度。
表7-7 初定的各段流道半径和长度

2)以塑料熔体的充模速率和压力损失校核流道尺寸。
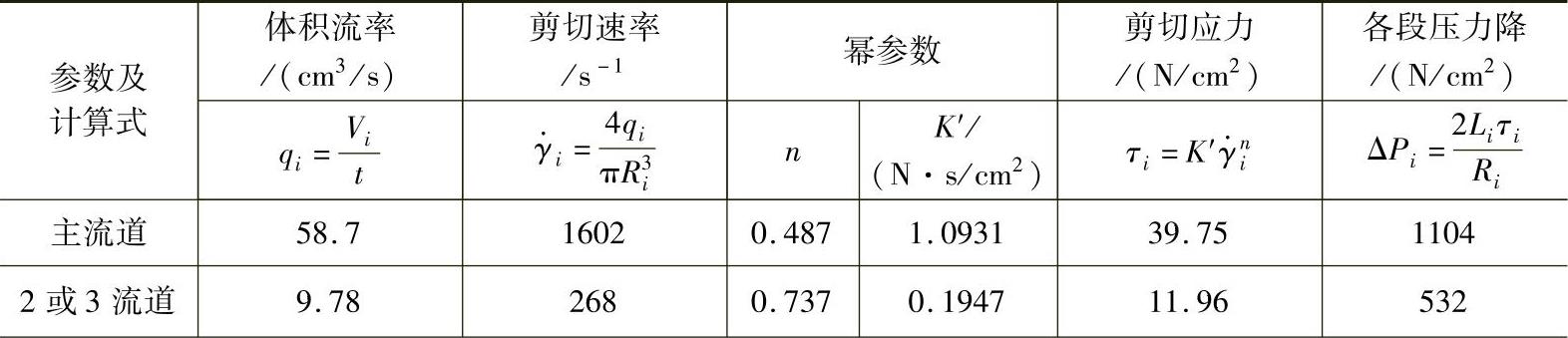
表7-7各段流道半径和长度进行压力降校核的最终结果见表7-8。
表7-8 对表7-7各段流道的压力损失计算校核
(续)

由于塑料熔体的非牛顿性,充模熔体在流道板各流程的注射点的输出压力相差很大,充模过程不平衡。
经流道2或3流程:(11.04+3.13+5.32)MPa=19.49MPa;
经流道5或6流程:(11.04+7.14+17.14)MPa=35.32MPa;
经流道8或9流程:(11.04+7.14+1.04+2.60)MPa=21.82MPa。
而且,如图7-14a所示,d4=12mm大于两头d1=9.1mm和d7=11.3mm,加工很困难。
3)以塑料熔体的流变平衡设计流道尺寸。
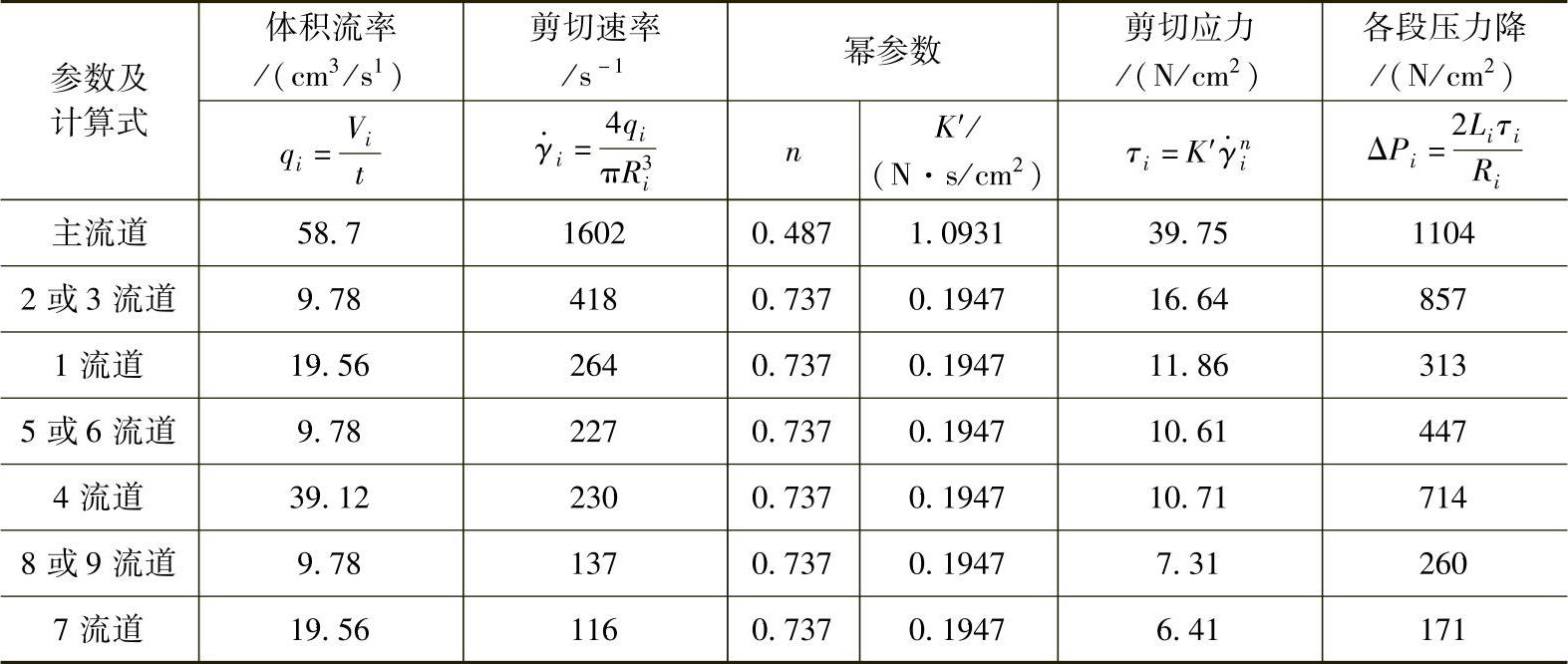
表7-9中的各段流道半径和长度进行压力降校核的最终结果见表7-10。充模熔体在流道板各流程的注射点的输出压力相等。
经流道2或3流程:(11.04+3.13+8.57)MPa=22.74MPa;
经流道5或6流程:(11.04+7.14+4.47)MPa=22.65MPa;
经流道8或9流程:(11.04+7.14+1.71+2.60)MPa=22.49MPa。
关于一模多腔非平布置流道系统的,流变平衡设计,有以下四条意见供参考:
①一模多腔流道系统的局部非平衡布置,可以笔算实现流变平衡,能缩短流道长度,可减小分流道层次,降低流道板高度。流变平衡设计和计算简便,与应用流动分析计算机软件相比可节省许多时间。
②一模多腔流道系统的完全非平衡布置可以用牛顿流体的流量平衡方程进行初步设计,然后用流变平衡方法进行修正,达到各注射点的压力基本相等。
③一模多腔流道系统的平衡布置也应该按流变平衡原理设计流道尺寸,使各级各段流道中输送塑料熔体的剪切速率和剪切应力基本不变,达到稳定流动的最好状态,也容易实现整个流道板温度均匀分布。
④一模多腔流道系统的非平衡布置达到流变平衡后各级各段流道中的剪切速率和剪切应力有变化,输送塑料熔体不是稳定流动。为了防止不良的流动状态,各段流道的流体剪切速率应限制在102~103s-1范围内。
表7-9 流变平衡的各段流道半径和长度

表7-10 对表7-9流变平衡的各段流道的压力损失设计计算
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




