非牛顿型塑料熔体的流动特性

塑料熔体在注射成型流动过程中的黏度变化极为复杂。本节介绍聚合物熔体的非牛顿型流动和流变曲线的测定。

1.非牛顿型流体流动

剪切流动按剪切应力与剪切速率的关系，可以分为牛顿型流体和非牛顿型流体的流动。

（1）牛顿型流动 流体流动时内部抵抗流动的阻力称为黏度，它是流体内摩擦力的表现。为了研究流体剪切流动的黏度，可将这种流体的流动简化成图3-1所示的层流模型。

图3-1所示的稳定的剪切流动出现在塑料熔体的注射过程中。如果采用直角坐标系，y=0处流体是静止的，y=h处的流体则以与上平面相同的速度v_max在x方向上运动。此种流动发生在两平行板间的窄缝之中。假如采用圆柱坐标系，则圆柱中央r=0处流体以v_max在x方向上运动，在r=R管壁上流动是静止的。此种流动发生在压力作用下的圆管道剪切流动中。

将这种切变方式的流动看作许多彼此相邻的薄液层沿外力作用方向进行的相对移动。图3-1中的F为外部作用于面积A上的剪切力。F克服面积A下各层的流体间的内摩擦力，使以下各层流体向右流动。单位面积上的剪切力称剪切应力，单位为Pa，剪切应力τ是流动方向的单位面积的剪切力，反映了流体内摩擦的黏滞阻力，有

图3-1 剪切流动的层流模型

流体以速度v沿剪切力方向移动，在黏性阻力和固定壁面阻力的作用下，使相邻液层之间出现速度差。假定液层对固定壁面无滑移，与壁面接触的液层的流动速度为零。在间距为dy的两液层面的移动速度分别为v和v+dv。dv/dy（或dv/dr）是垂直液流方向的速度梯度，称为剪切速率，以表示，其单位为s^-1，有

设液体运动方向为x轴正向，运动距离dx与相应的移动时间dt之比为速度，即v=dx/dt，则速度梯度为

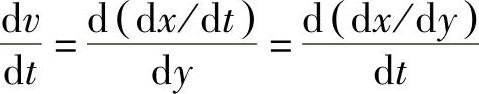
因此，剪切速率也可理解成间距为dy的液层在dt时间内的相对移动距离，或者在单位时间内剪切力作用下液体产生的剪切应变。

理想黏性流体的流动符合牛顿型流体的流变方程。遵循牛顿黏性定律的牛顿型流体，其剪切应力与剪切速率成正比，有

式（3-3）中，比例系数μ为牛顿黏度，单位为Pa·s（1Pa·s=1N·s/m²）。它是流体本身所固有的性质，其大小表征抵抗外力所引起的流体变形的能力，反映了物料流体的流动性优劣。

剪切应力τ与剪切速率的关系曲线也称为流动曲线或流变曲线，如图3-2所示。牛顿型流动曲线是通过原点的直线。该直线与轴夹角θ的正切值是流体的牛顿黏度，即

牛顿流体的应变是不可逆的。纯黏性流体流动的特点是在其应力解除后应变永远保持。牛顿黏度与温度有密切关系。真正属于牛顿流体的只有低分子化合物的液体或溶液，如水和甲苯等。

图3-2 各种类型流体的流动曲线

a—膨胀性流体 b—牛顿流体 c—假塑性流体

（2）非牛顿型流动 图3-2所示的流动曲线a和c，其流体的剪切应力和剪切速率之间呈现非线性的曲线关系。所有不服从牛顿黏性定律的流体称为非牛顿流体。这些流体在一定的温度下，其剪切应力和剪切速率之间不成正比关系。其黏度不是常数，而是随剪切应力或剪切速率而变化的非牛顿塑料熔体的表观黏度η_a，如图3-3所示。

假塑性流体是非牛顿流体中最常见的一种。橡胶和绝大多数聚合物及其塑料的熔体和浓溶液都属于假塑性流体。如图3-2曲线c所示，此种流体的流动曲线是非线性的，剪切速率的增加比剪切应力增加得快。又如图3-3曲线c所示，此种流体的流变曲线的特征是黏度随剪切速率或剪切应力的增大而降低，常说成是剪切变稀的流体。聚合物的细长分子链在流动方向的取向使黏度下降。

膨胀性流体的流动曲线如图3-2曲线a所示，其剪切速率的增大比剪切应力的增大要慢一些。又如图3-3曲线a所示，此种流体的流变曲线的特征是黏度随剪切速率或剪切应力的增大而升高，常说成是剪切增稠的流体。聚合物熔体与固体颗粒填料体系等属于此种流体。在较高剪切速率下碳酸钙填充的塑料熔体具有膨胀性。在静止状态，固体粒子密集地分布在液相中，能较好地排列并填充在间隙中。在以高剪切速率流动时，颗粒沿着各自的液层滑动，不进入层间的空隙，出现膨胀性的黏度增加。

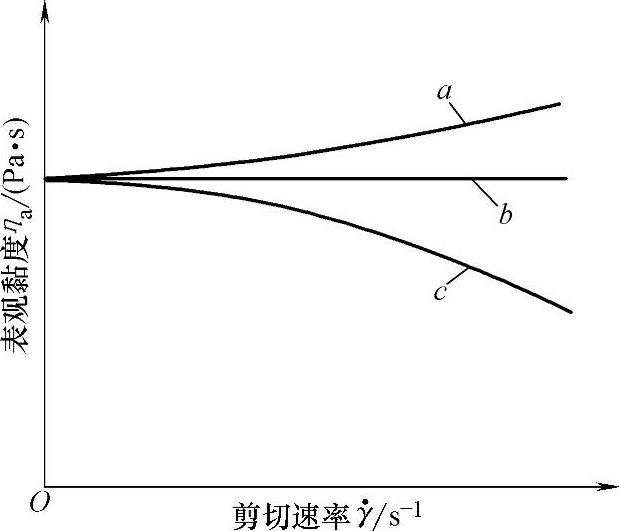
图3-3 各种类型流体的流变曲线

a—膨胀性流体 b—牛顿流体 c—假塑性流体

描述假塑性和膨胀性的非牛顿流体的流变行为用幂律函数方程表示，即

式中 K——流体稠度（Pa·s）；

n——流动指数，也称非牛顿指数。

流体稠度K值越大，流体越黏稠。流动指数n可用来判断流体与牛顿型流体的差别程度。n值离整数1越远，则呈非牛顿型越明显。对于牛顿流体，n=1，此时K相当于牛顿黏度_μ；对于假塑性流体，n<1；对于膨胀性流体，n>1。

将幂律函数方程与牛顿流体的流变方程进行比较，有

令

得

式中 η_a——非牛顿型塑料熔体的表观黏度（Pa·s）。

2.流变曲线

注射成型是将塑料熔体在一定压力下，经流动充填模具型腔来实现的。塑料熔体有比一般流体高得多的黏度，通常为10²～10³Pa·s，并且有非牛顿型的假塑性流体的特征。

生产中通常用黏度的相对值来评估熔体的流动性。热塑性塑料熔体流动速率试验方法使用最普遍的是国家标准GB/T3682中的方法。熔体流动速率[熔体流动速率（g/10min），缩写MFR或MFI]是在一定温度和负荷下，10min通过标准口模的熔体质量。口模内径为2.095mm，长为8mm。负荷用的砝码及机筒自动控制的温度均要按标准条件进行。注射模适宜浇注的塑料熔体熔体流动速率为5～50g/10min。

图3-4 毛细管流变仪

1—口模 2—聚合物 3—柱塞 4—机筒 5—热电偶 6—加热器 7—加热盘 8—支框 9—负重 10—机架

塑料熔体的流动速率测量方便，检测仪器简单，数据容易获得。它是工业企业对熔体黏度的相对测定法，但此数据不能用于熔体流动的黏度、体积流率、剪切应力、剪切速率及流程压力损失的计算。塑料熔体的黏度特性要用流变仪测得，常用图3-4所示毛细管流变仪在压力作用下进行剪切流动有关流变参数的测定和分析。熔体流动速率仪的口模长径比（L/D）比较小，L/D大约为4，而毛细管流变仪的L/D大致为20～40。熔体流动速率仪是对挤出物称重得知流量，而流变仪上装有传感器，可测出活塞杆的压力和位移，又经自动计时，可获知柱塞下降速度，从而推算出熔体流经口模的流量，而且它的载荷和柱塞速度有很大的调节范围。

图3-5 聚丙烯的流变曲线

a）剪切应力τ与剪切速率流变曲线 b）表观黏度η_a与剪切速率流变曲线MFI=10.8g/10min毛细管L/D=40/1

测量时，将恒定压力作用在柱塞上，把装在机筒里经熔化的物料从毛细管中挤出，测得柱塞的下移速度。由流量、压力、温度和毛细管几何参量，可获得如图3-5所示的流变曲线。常见的有毛细管剪切应力τ与剪切速率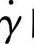的流变曲线（见图3-5a）和表观黏度η_a与剪切速率的流变曲线（见图3-5b）。

利用实验室的毛细管流变仪，可测得图3-5所示的流变曲线。有了这些流变曲线，并经流动方程的分析计算，能解答注射模中塑料流动的工程问题，能分析计算模具流道和型腔中熔体流动的剪切速率和剪切应力，能计算预测各段流程的压力损失，从而校核设计计算流道尺寸和型腔间隙等。国内外市场上出现的注塑流动分析模拟CAE/CAD计算机软件，就是经实验储存了各种塑料品种的流变曲线参量，这些参数可用来优化塑料件和注射模设计以及注射加工工艺的拟定。

注射充模的热塑性塑料熔体的黏度不但与温度和压力有关，而且随流动的剪切速率增大而下降，有“剪切变稀”的现象，如图3-5b中的曲线所示，即表观黏度η_a随增大而下降。因此，非牛顿流体的流变方程以流动指数n来描述。

熔体在圆管中流动时，若τ为管壁的最大剪切应力，有

式中 Δp——管道两端的压力差（Pa）；

R——管径（m）；

L——管道长度（m）。

变换式（3-6a）的形式，还可用来求塑料熔体在圆管流道中流动的压力损失，即

为管壁上剪切速率，也称作表观剪切速率，有

(www.xing528.com)

式中 Q——体积流率，可用被充模的型腔体积V与注射机常规充模时间t之比求得。

近年来，国内在流道和型腔充模流动分析的工程计算时，为应用流变数据的方便，常用式（3-8）来计算τ：

式中 K′——表观稠度（Pa·s）。

从流变仪测得的数据为表观的稠度、黏度和剪切速率。“表观”一词常冠以实验测定的流变参量。在一定条件下，只能片面或局部地观察到流变参量，故要经过修正，才能获知真实的稠度、黏度和剪切速率。用毛细管流变仪测定的非牛顿流体的流变曲线，需做两项修正才能成为真实的流变曲线。其中，一项是非牛顿修正，又称雷比诺维茨修正；另一项是入口修正，又称贝格里修正。

在未修正的流变曲线上可获知K′。不过真实值与表观值相差不大，在工程计算时可以忽略差异。K′与K有如下关系：

表观稠度K′与流体稠度K相差不大，当n=0.1时，有

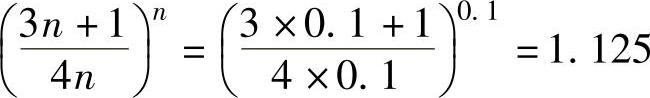
当n=0.9时，有

3.流变曲线上获得表观稠度K′和近似n值

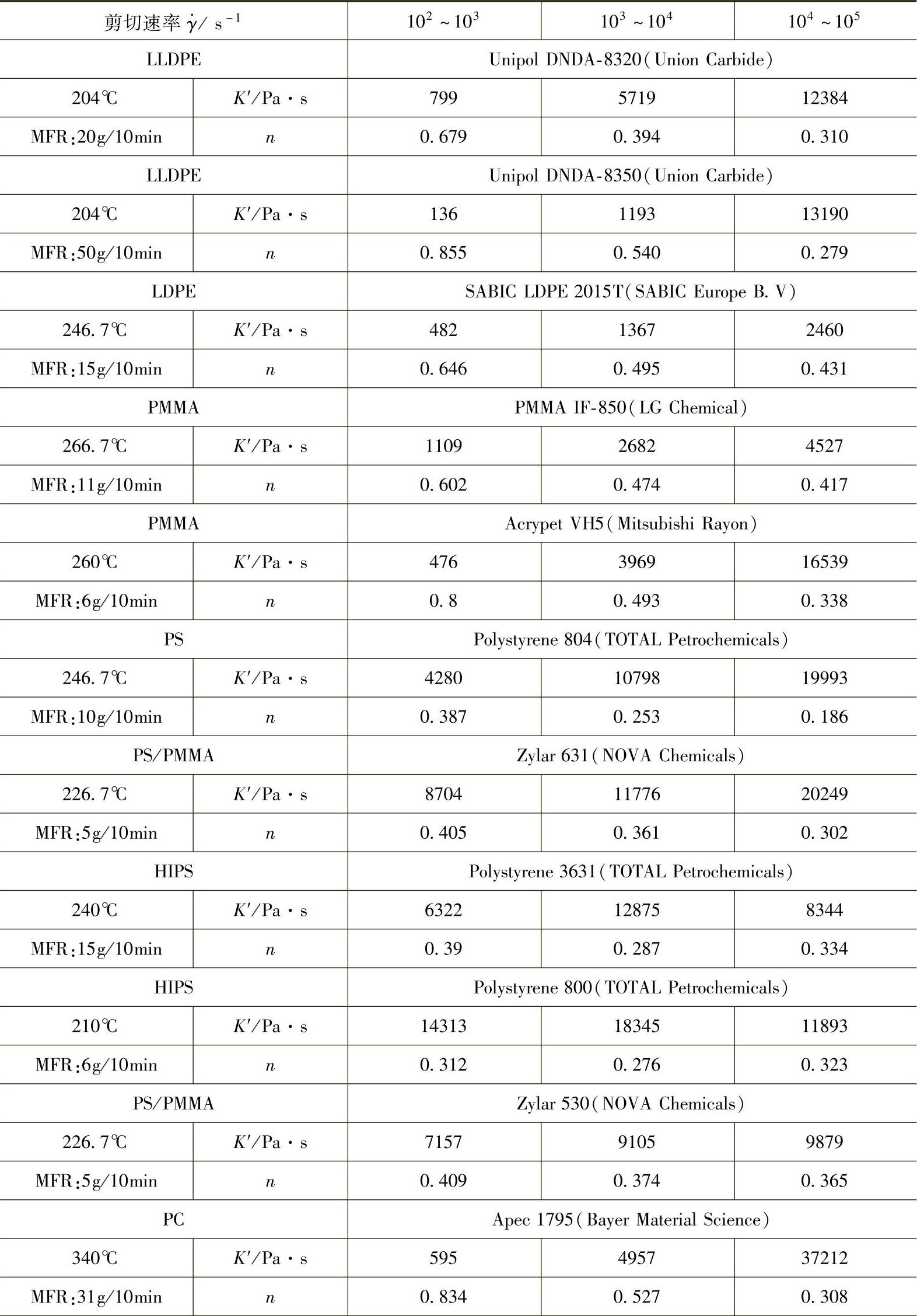
聚合物熔体在工程上的实用计算方程，用K′和n描述也就是用流变的表观参量来进行运算，这样，数据不经修正处理，来源方便。工程上还习惯将剪切速率范围内的流变曲线视为小段直线。在此区间内有一定的表观稠度K′和近似n值。表3-1列出了我国20世纪末实测的塑料熔体的表观稠度K′和流动指数n的数据。熔体流变数据单位用N-m-s，对于制品和模具设计很不方便，因此常用N-cm-s，黏度单位用N·s/cm²。表3-1中，表观稠度K′单位Pa·s=10^-4N·s/cm²。

表3-1 塑料熔体的表观稠度K′和流动指数n

（续）

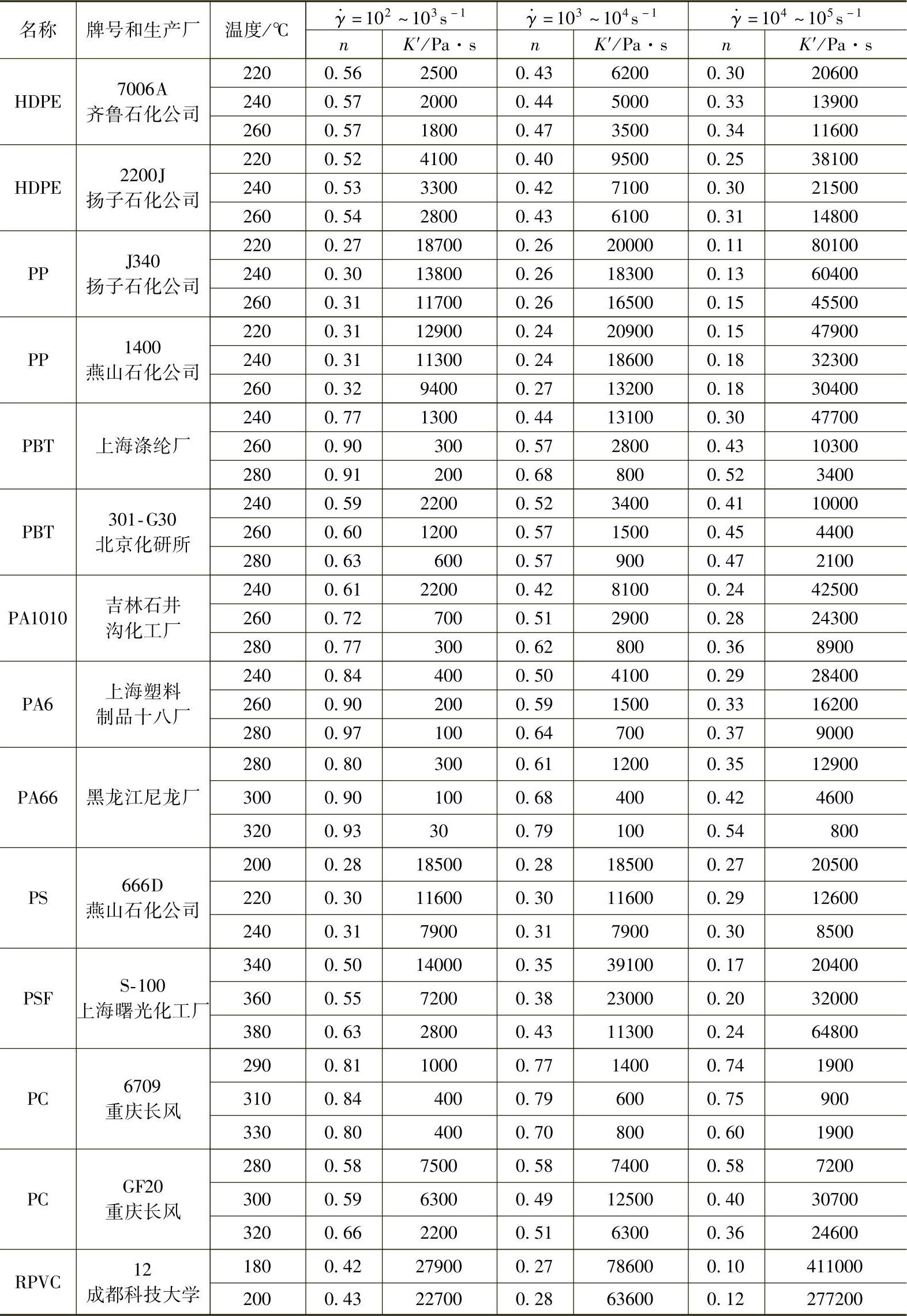
图3-6所示的流变数据用先进的注射机上的流变仪测得，并储存于计算机的专业数据库中。用这种表观黏度η_a与剪切速率的流变曲线，可以求出剪切速率某区间内的表观稠度K′和流动指数n。得到表3-2所列的数据后，可方便用于人工的流变学计算。

图3-6 ABS的表观黏度η_a与剪切速率的流变曲线

MFI=13g/10min

从图3-6所示的ABS的流变曲线可以求得其K′和n，步骤如下：

1）读220℃剪切速率对应的表观黏度_ηa值。

对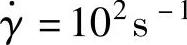，读实际值和坐标区间值，将比值经指数运算，得

η_a1=10^3.105263Pa·s=1274Pa·s

对，读实际值后，经指数运算，得

η_a2=10^2.4210526Pa·s=264Pa·s

2）由两点的联立方程求解K′和n。

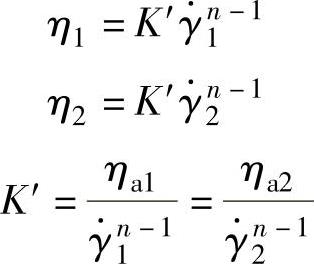
代入_ηa1和η_a2、和数值后，得

解此方程，得

n=0.316=0.32

代入方程，得

3）校核后取平均值。

得剪切速率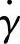在10²～10³s^-1区间内。

n=0.32

K≈K′=2.91×10⁴Pa·s

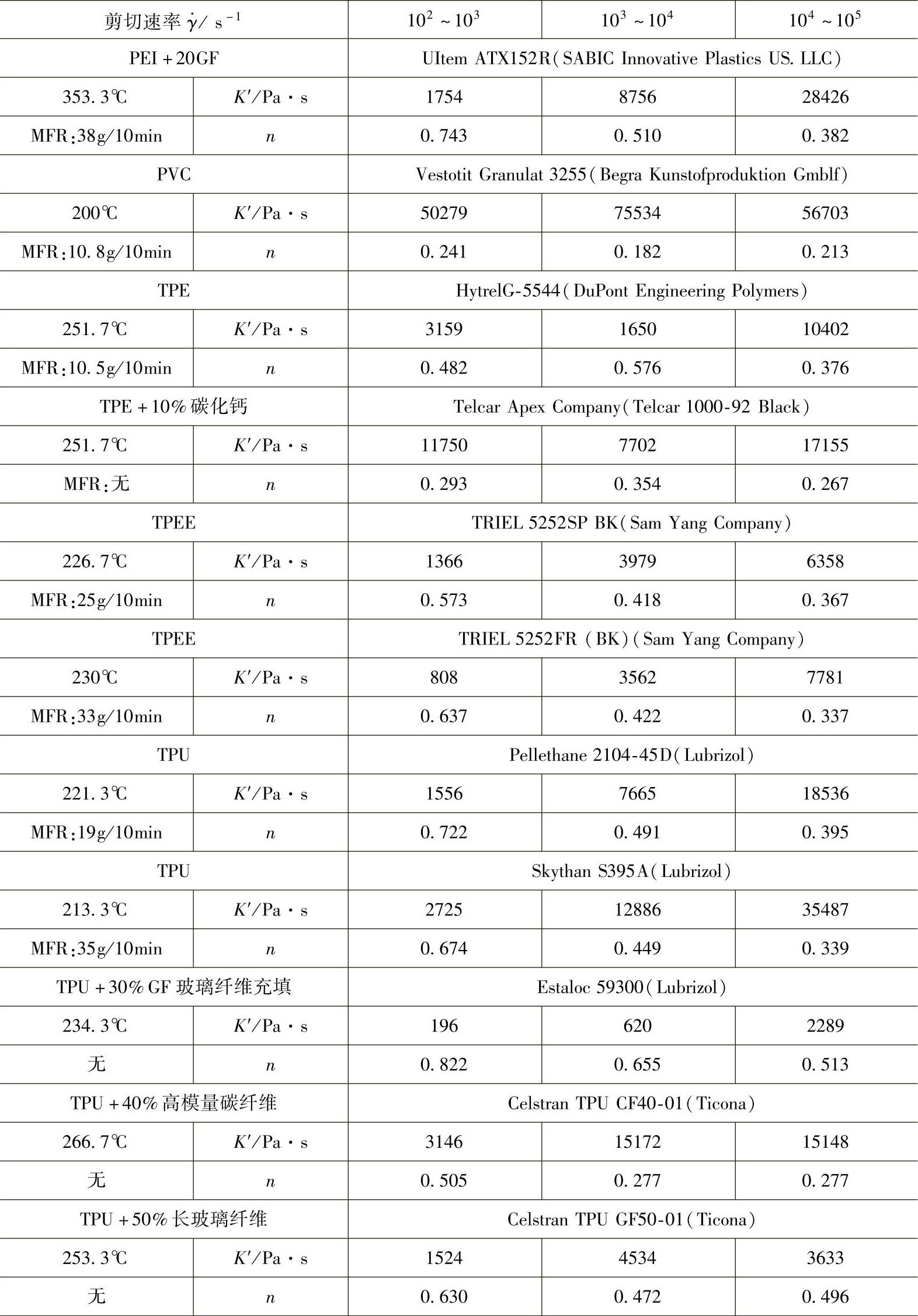
表3-2 一些国外塑料的表观稠度K′和流动指数n

（续）

（续）

（续）

（续）

（续）

（续）

（续）

在注塑件的设计中，应该将塑件成型型腔和注射模具的浇注系统一起考虑，并做流变学和传热学分析。现有的各种流动分析方法可以经人工计算，获知在充模过程中和流程各位置的体积流率、剪切应力与剪切速率、各段流程的压力损失，从而在以下两个方面避免塑件形状和尺寸的不良设计。

1）要保证注射充模时熔体具有合理的剪切速率。塑料熔体在模具通道间隙中的剪切速率应为10²～10⁴s^-1。过低充模速率会使熔体流动性变差。过高的剪切速率在型腔内会出现湍流或涡流，会产生熔体喷射并且破碎，将成型废次的注塑件。熔体在模内流动应是雷诺数很低的层流。

2）要保证型腔的充模压力。塑料熔体的压力传递能力较差，流经各流程的流道和浇口后，压力逐渐下降会使注射到塑件型腔的熔体压力不足。进入塑件型腔的熔体压力应有（250～500）×10⁵Pa。为此，一方面浇注系统的流道要有足够的截面尺寸，另一方面，塑件型腔流程不能太长又薄，以免使料流末端的压力不足，造成注塑件密度低、收缩率大，严重的甚至不能注满。因此，必须由各种塑料熔体的流程比来校核塑件的壁厚，必须将浇注系统中的熔体输送压力损失限制在350×10⁵Pa以下。

众所周知，对注射模塑进行计算机模拟，是流动和冷却分析先进和有效方法。现代注射成型计算机辅助工程CAE（Computer Aid Engineering）软件能辅助设计注射制品和模具。它是决策性的软件，能将注塑件设计、模具设计、注射工艺拟订、试模、注射依次进行数值分析，并可进行反复修改及优化，直观地在计算机屏幕上模拟出实际成型过程，预测塑件设计对产品的影响，直接观察到塑件上熔合缝和气囊的位置，预见注塑件成型时的剪切速率、温度场和压力场，判断塑件上密度不足、凹陷和注不满等缺点，为改进注塑件和模具设计提供科学依据。

但是，计算机模拟的前提是计算机造型，应让计算机获知注塑件和浇注系统所有形体和尺寸的信息，然后用有限元数值分析方法将形体离散化，进行网格划分。常用的是二维流动模型的分析方法。将三维的塑件展平，有分支地展成若干个流程，将圆管件、圆板件、平板件或圆环板件相互串联。因为塑料注射件是薄壁板的组合件，故二维的计算机浇注系统模拟应用广泛。在应用CAE软件辅助设计注塑件和模具时，对分型面、流道的分布和尺寸、浇口的形式和位置，设计师应该有所考虑。