LNG是以甲烷为主,包括氮、乙烷、丙烷等组分的低温液体混合物,与外界环境存在着温度差和压力差。其冷量即为LNG变化到与外界平衡状态所能获得的能量,所以采用 的概念可以对LNG的冷量进行评价[4]。
的概念可以对LNG的冷量进行评价[4]。
LNG是以甲烷为主,包括氮、乙烷、丙烷等组分的低温液体混合物,与外界环境存在着温度差和压力差。其冷量即为LNG变化到与外界平衡状态所能获得的能量,所以采用 的概念可以对LNG的冷量进行评价[4]。
的概念可以对LNG的冷量进行评价[4]。
LNG的冷量 ex可分为压力p下由热不平衡引起的低温
ex可分为压力p下由热不平衡引起的低温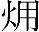 ex,th和环境温度下由力不平衡引起的压力
ex,th和环境温度下由力不平衡引起的压力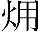 ex,p,即
ex,p,即
ex(T,p)=ex,th+ex,p (7-1)
其中
ex,th=ex(T,p)-ex(T0,p) (7-2)
ex,p=ex(T0,p)-ex(T0,p0) (7-3)
LNG的冷量 ex可分为压力p下由热不平衡引起的低温
ex可分为压力p下由热不平衡引起的低温 ex,th和环境温度下由力不平衡引起的压力
ex,th和环境温度下由力不平衡引起的压力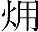 ex,p,即
ex,p,即
ex(T,p)=ex,th+ex,p (7-1)
其中
ex,th=ex(T,p)-ex(T0,p) (7-2)
ex,p=ex(T0,p)-ex(T0,p0) (7-3)
LNG在定压下由低温升高到T0的过程中发生沸腾相变。设LNG为在温度Ts下处于平衡状态的两相物质,汽化热为r,相应潜热炯为 ,加上从Ts到T0气体吸热的显热
,加上从Ts到T0气体吸热的显热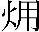 ,则其低温
,则其低温 ex,th为
ex,th为
LNG在定压下由低温升高到T0的过程中发生沸腾相变。设LNG为在温度Ts下处于平衡状态的两相物质,汽化热为r,相应潜热炯为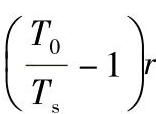 ,加上从Ts到T0气体吸热的显热
,加上从Ts到T0气体吸热的显热 ,则其低温
,则其低温 ex,th为
ex,th为
压力 ex,p为
ex,p为
压力 ex,p为
ex,p为
LNG是低温多组分液体混合物,其相变潜热、平均泡点温度等与压力、组分等有密切关系。汽化后的气体如压力较高,则性质偏离理想气体。因此,要对式(7-4)和式(7-5)进行计算,必须建立LNG相平衡关系,采用真实流体状态方程进行分析。
RKS方程形式虽然简单,但用于轻烃混合物气液相逸度及其他有关热力学性质时,却能获得较高精度。RKS方程标准形式如下:
LNG是低温多组分液体混合物,其相变潜热、平均泡点温度等与压力、组分等有密切关系。汽化后的气体如压力较高,则性质偏离理想气体。因此,要对式(7-4)和式(7-5)进行计算,必须建立LNG相平衡关系,采用真实流体状态方程进行分析。
RKS方程形式虽然简单,但用于轻烃混合物气液相逸度及其他有关热力学性质时,却能获得较高精度。RKS方程标准形式如下:
其中
其中
式中,p是压力(Pa);Rg是气体常数[J/(kg·K)];T是温度(K);v是比体积(m3/kg);a、b是与气体种类有关的常数;ω是物质的偏心因子;下标cr表示临界点的值。
多项式形式为
Z3-Z2+(A-B-B2)Z-AB=0 (7-7)
其中
Z=pv/(RgT);A=ap/(RgT)2;B=bp/(RgT)
式中,Z是压缩因子。
用于混合物时,式(7-6)中的系数如下:
式中,p是压力(Pa);Rg是气体常数[J/(kg·K)];T是温度(K);v是比体积(m3/kg);a、b是与气体种类有关的常数;ω是物质的偏心因子;下标cr表示临界点的值。
多项式形式为
Z3-Z2+(A-B-B2)Z-AB=0 (7-7)
其中
Z=pv/(RgT);A=ap/(RgT)2;B=bp/(RgT)
式中,Z是压缩因子。
用于混合物时,式(7-6)中的系数如下:(https://www.xing528.com)
式中,zi、zj是混合物中i、j组分的摩尔分数;kij是二元交互作用系数,一般由实验来确定。
当用状态方程求解多元气液相平衡时,气液相温度和压力相等,各种组分化学势相等。因此各种组分在各相逸度也相等,即
式中,zi、zj是混合物中i、j组分的摩尔分数;kij是二元交互作用系数,一般由实验来确定。
当用状态方程求解多元气液相平衡时,气液相温度和压力相等,各种组分化学势相等。因此各种组分在各相逸度也相等,即
则
则
式中, 是溶液中i组分的逸度和逸度系数;xi、yi是溶液中i组分的气相摩尔分数、液相摩尔分率,∑xi=∑yi=1,zi=(xi+yi)/2;Ki是气液相平衡常数。
是溶液中i组分的逸度和逸度系数;xi、yi是溶液中i组分的气相摩尔分数、液相摩尔分率,∑xi=∑yi=1,zi=(xi+yi)/2;Ki是气液相平衡常数。
将RKS方程代入,可得
式中, 是溶液中i组分的逸度和逸度系数;xi、yi是溶液中i组分的气相摩尔分数、液相摩尔分率,∑xi=∑yi=1,zi=(xi+yi)/2;Ki是气液相平衡常数。
是溶液中i组分的逸度和逸度系数;xi、yi是溶液中i组分的气相摩尔分数、液相摩尔分率,∑xi=∑yi=1,zi=(xi+yi)/2;Ki是气液相平衡常数。
将RKS方程代入,可得
对于气液两相,当液相组分的摩尔分数xi和系统压力p给定后,可得到气液平衡对应的泡点温度Ts和气相组成的摩尔分数yi。
汽化热即为气相与液相之间焓差。对真实流体,焓可由剩余函数求得。由RKS方程可得剩余摩尔焓为
对于气液两相,当液相组分的摩尔分数xi和系统压力p给定后,可得到气液平衡对应的泡点温度Ts和气相组成的摩尔分数yi。
汽化热即为气相与液相之间焓差。对真实流体,焓可由剩余函数求得。由RKS方程可得剩余摩尔焓为
其中
其中
对相平衡气液两相,Himd相同,因此汽化热即是此偏离函数之差值,即
r=Hv,m-Hl,m=(Hidm-Hm)l-(Hidm-Hm)v (7-14)
真实气体摩尔定压热容为
Cp,m=C0p,m+ΔCp,m (7-15)
其中
对相平衡气液两相,Himd相同,因此汽化热即是此偏离函数之差值,即
r=Hv,m-Hl,m=(Hidm-Hm)l-(Hidm-Hm)v (7-14)
真实气体摩尔定压热容为
Cp,m=C0p,m+ΔCp,m (7-15)
其中
式中,Aj、Bj、Cj、Dj是j组分理想气体摩尔热容方程的各常数;ΔCp,m通过焓差微分求得。
式中,Aj、Bj、Cj、Dj是j组分理想气体摩尔热容方程的各常数;ΔCp,m通过焓差微分求得。
将Ts、r、cp等代入式(7-4),即可得LNG低温 。而压力
。而压力 为
为
将Ts、r、cp等代入式(7-4),即可得LNG低温 。而压力
。而压力 为
为
将RKS方程代入积分,可得
将RKS方程代入积分,可得
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




