天然气的传输特性，天然气的粘度

天然气的传输特性是天然气传热和流动阻力计算的关键数据，在模拟与天然气输送、液化、储存相关的生产过程时，需要有能应用于烃混合物及过程条件的范围很大的迁移性质关联式。天然气液化流程中不可避免地存在着流体的流动、不同工质间的传热传质问题，为了更合理有效地发挥各流程设备的作用，需要了解天然气在不同工况下的流动和传热传质特性，而这些也需要有精确的天然气迁移物性数据作为保证。

粘度、热导率和扩散系数，是液化天然气传输特性的主要决定因素，在涉及到动量、热量和质量传递计算的场合发挥着重要作用，是液化天然气流动和传热计算的关键数据，也是天然气输送、储存相关过程的计算、分析及设计时首先需要精确知道的参数。

1.天然气的粘度

（1）常用粘度计算方法综述天然气的粘度计算涉及到天然气的气态、液态的粘度预测，因此首先分别对常用的气态、液态粘度计算方法进行评述。用于气体粘度估算较好的方法有Chung、Lucas、Reichenberg等法，对于非极性物，误差约0.5%～1.5%，对于极性物，误差约2%～4%。Lucas法和Chung法可用于非极性和极性化合物，Reichenberg法主要针对有机物。高压气体的计算则要考虑压力对气体粘度的影响，对上述算法进行修正或采用剩余粘度法计算。

关于液体粘度的理论研究很多，但是目前液体粘度和热导率的理论计算方法十分复杂，需要多个特性参数，难以直接计算。工程上，一般可以采用经验公式或关联式计算。与气体粘度相反，液体粘度随温度升高而减小。低于常沸点时，可采用Andrade方程关联；高于常沸点时，可用Antoine方程关联。在液体粘度的计算模型中，当T_r＜0.75K时，以Van Velzen的基团贡献法和Przeziecki-Sridhar的对应状态法较好；T_r＞0.75K时，宜用Letsou-Stiel法。总的说来，上述模型计算误差均偏大，一般在10%～15%。

中、低压力下，压力对液体粘度的影响较小。随压力的增大，其影响逐渐增大。压力的影响还与温度有关，温度越低，压力影响越大。目前尚无成熟的理论预测压力对粘度的影响规律，主要有一些经验、半经验关联式，如Barus方程、Eyring方程、Dymond模型等。液体混合物的粘度和组成之间一般无直线关系，有时还会出现极大值和极小值甚至S曲线关系，目前尚难理论预测。

综合来说，低压天然气的粘度计算较为准确的算法有Chung法和Lucas法，高压天然气的计算要考虑压力对气体粘度的影响，采用修正后的Chung和Lu-cas高压粘度模型或剩余粘度法计算；液化天然气的粘度计算则以Jamieson经验关联式与Teja-Rice法结合使用较好。由于天然气为多组分混合物，计算混合物的迁移性质时要考虑组分的影响。有关纯组分迁移性质计算的算法很多，而能适用于混合物迁移物性计算的算法则相对较少，所以最直接有效的方法，就是在纯物质迁移性质计算的基础上，通过引入混合规则，将混合物看做具有一套按一定规则求出的虚拟临界参数、性质均一的虚拟纯物质，进而关联混合物迁移性质与组成的关系。这种方法能够准确地预测宽广范围内的混合物迁移性质，已成为混合物物性计算的最重要手段。

（2）混合规则的选取 混合规则是把混合参数Q_m表示为混合物组成和纯组分参数的关系式：

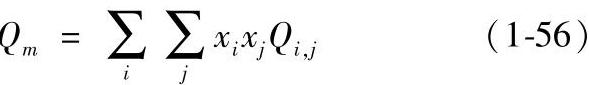
式中，x_i，x_j是组分i，j的摩尔分数。

根据纯物质参数Q_i确定混合物参数Q_m有三种常用的组合方式，即线性组合、平方根组合、洛伦兹组合。混合规则的确定，通常要先从理论上提出模型，然后根据混合物的实验数据，利用分析及数学方法，拟合混合物的参数与纯物质参数间的关系。混合规则的优劣，最终由它是否正确反应混合物的实验结果鉴定。一般而言，混合物迁移物性的混合规则是与其相关的算法紧密联系的。目前，天然气混合物迁移物性计算中主要的混合规则有Lucas混合规则、Chung混合规则和Teja对应态混合规则，下面分别加以说明。

1）Lucas混合规则

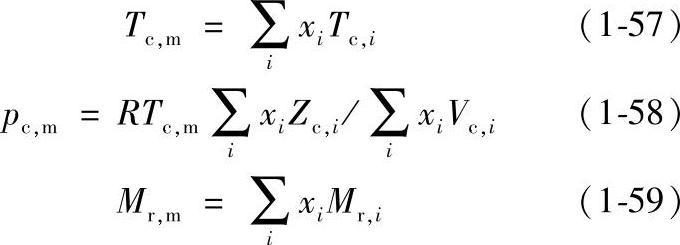
式中，T_c，m是混合物的虚拟临界温度；p_c，m是混合物的虚拟临界压力；Z_c，i是组分i的临界压缩因子；T_c，i为组分i的临界温度；V_c，i是组分i的临界摩尔体积；M_r，m是混合物相对分子质量；M_r，i是组分i的相对分子质量；x_i是组分i的摩尔分数。

2）Chung混合规则

T_c，m=1.2593（ε/κ）_m （1-60）

V_c，m=（σ_m/0.809）³ （1-61）

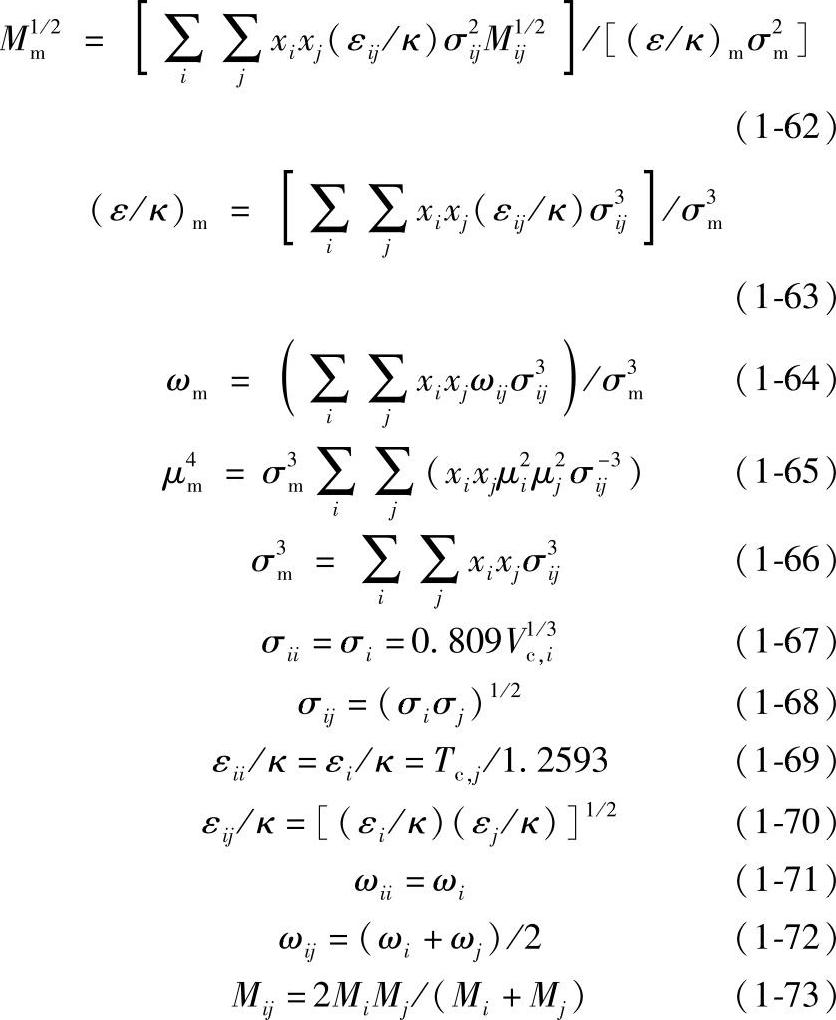
式中，V_c，m是混合物虚拟临界摩尔体积；ω_m是混合物偏心因子；μ_m是混合物偶极矩；σ_m是混合物碰撞直径。

3）Teja对应态混合规则

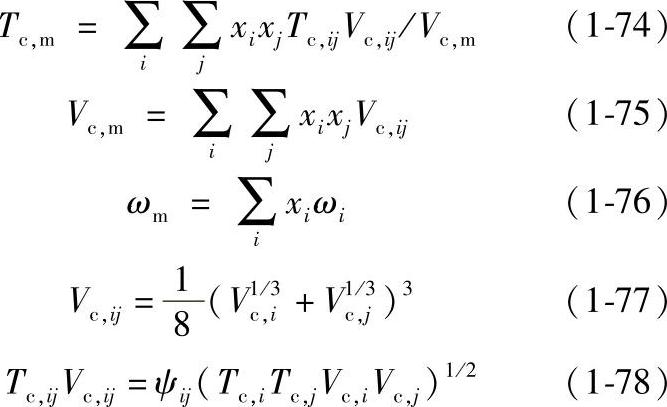
式中，ψ_ij是相互作用因子，必须由实验数据回归确定；ω_m是混合物偏心因子。

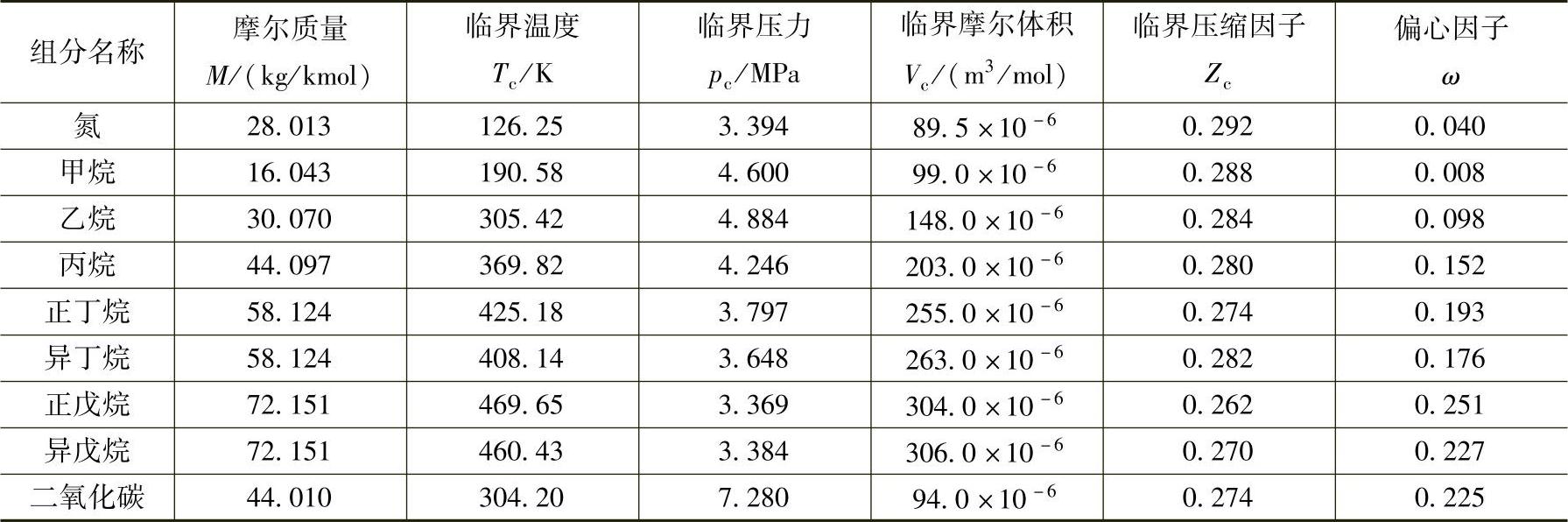
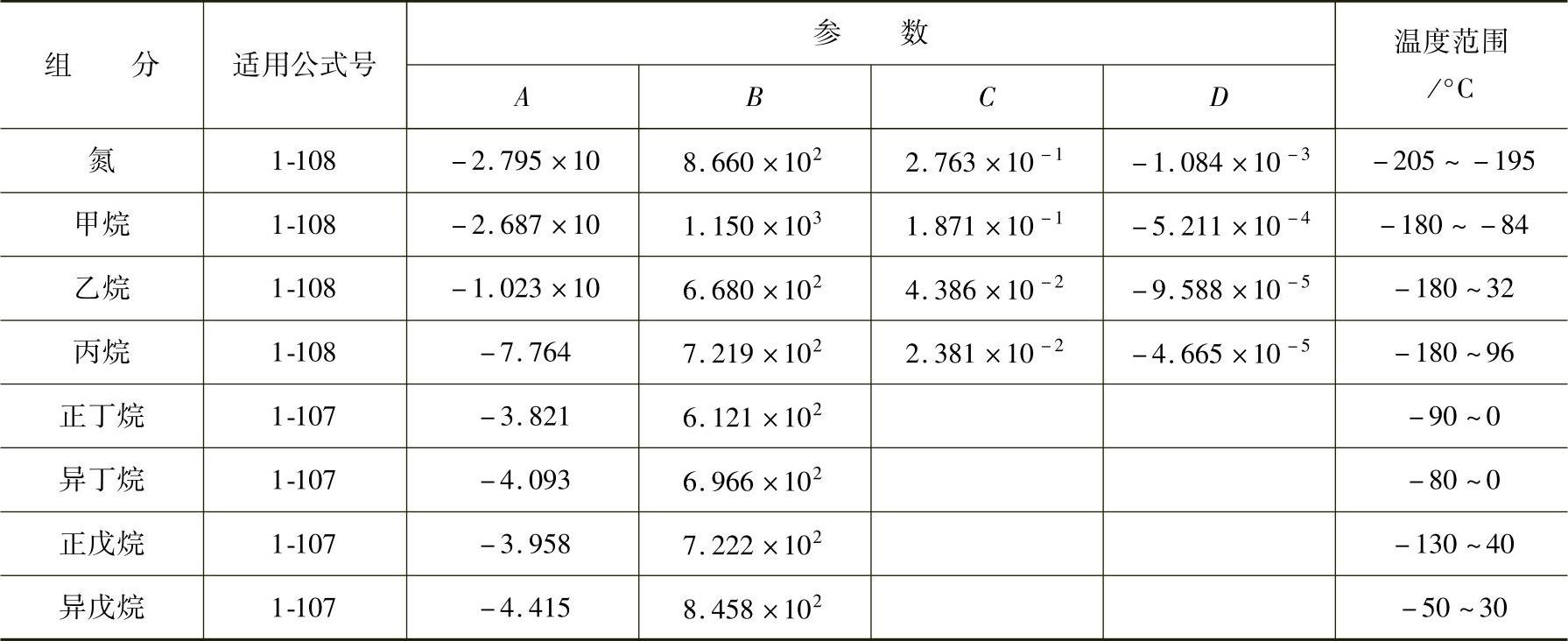
混合规则所需要的天然气常见组分特性参数见表1-20。

表1-20 天然气组分物性数据表

（3）不同压力范围的天然气的粘度计算

1）气体粘度压力修正界限的判别准则。气体压力对气体粘度影响很大，在临界点附近以及对比温度T_r为1～2时，气体粘度随压力的上升而增加；当对比压力很大时，可使气体粘度随温度升高而降低。因此，高、低压气体粘度的计算公式不同，需要考虑压力对气体粘度的影响。为此，首先需要确定气体粘度压力修正的界限。天然气在压力p、温度T下的对比压力、对比温度分别为

p_r，m=p/p_c，m （1-79）

T_r，m=T/T_c，m （1-80）

式中，p_r，m、T_r，m是混合物的虚拟对比压力和对比温度。

由气体修正粘度可得如下判别准则：

p_r，m＞0.188T_c，m （1-81）

高压气体混合物以式（1-81）为界限。压力低于此限，可忽略压力对气体粘度的影响。

2）低压天然气的粘度计算公式。低压气体粘度计算公式较好的有Lucas法和Chung法^[1]。

①Lucas法

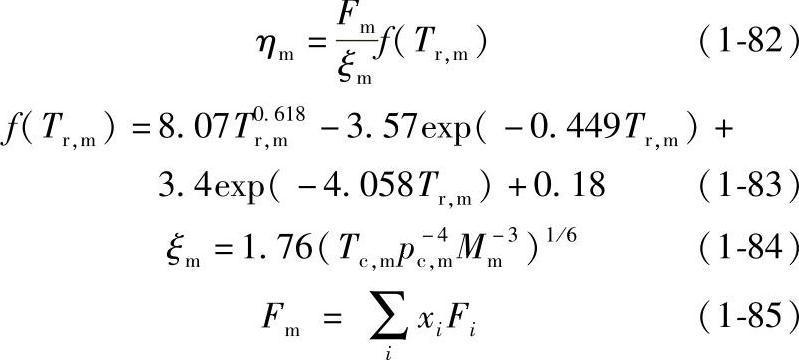
式中，η_m是混合物的粘度；F_m是极性气体的校正系数；M_m是混合物相对分子质量。

混合物的参数计算采用式（1-82）至式（1-85）的Lucas混合规则。

②Chung法

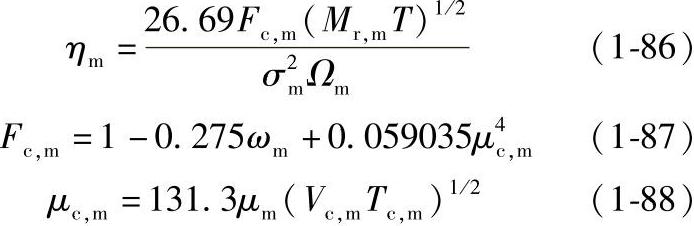
式中，F_c，m是极性气体的校正系数；M_r，m是混合物相对分子质量；σ_m是混合物的碰撞直径；Ω_m是混合物碰撞积分；ω_m是混合物的偏心因子；μ_m是混合物偶极矩。

混合物的参数计算采用式（1-86）至式（1-88）的Chung混合规则。

3）高压天然气的粘度计算公式。高压气体粘度较好的计算公式有修正后的Lucas法、Chung法和剩余粘度法。

①修正后的Lucas法

式中，K是压力修正相，定义为对比压力、对比温度的函数；η_pm是高压气体混合物粘度；F_pm是高压下极性气体的校正系数；ξ_m是混合物的粘度对比化参数；Y是修正系数；a、b、c是与气体种类有关的常数。

计算时不需要求解混合物密度。η_m由式（1-82）计算。

②修正后的Chung法

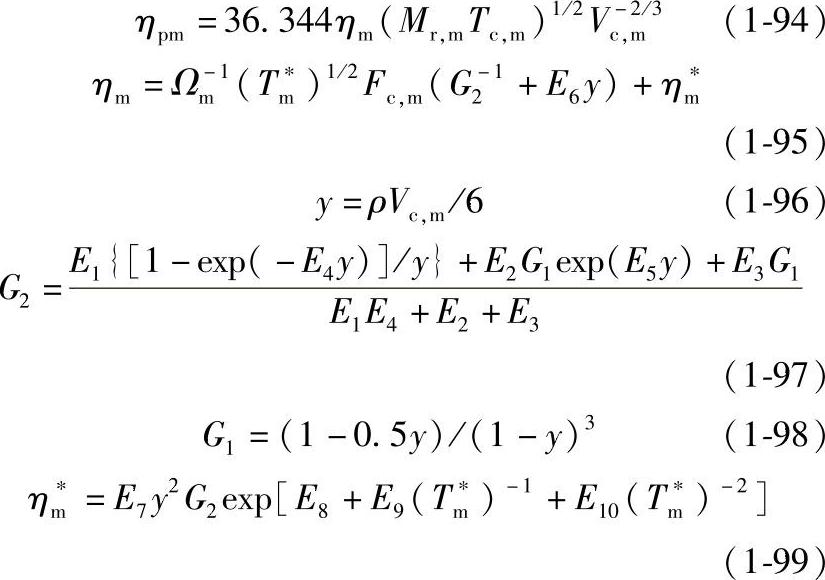
Chung法将压力修正项定义为气体密度的函数，计算中需要混合物密度值。式中，E₁～E₁₀为偏心因子ω、无量纲偶极矩μ_r及缔合因子κ的线性函数。G₁、G₂为计算方便定义的函数，

③剩余粘度法

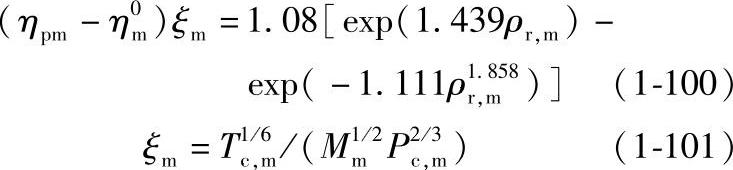
式中，η_pm是高压气体混合物粘度；η⁰_m是低压气体混合物粘度；ρ_r，m是虚拟混合物对比密度。

剩余粘度法混合规则为

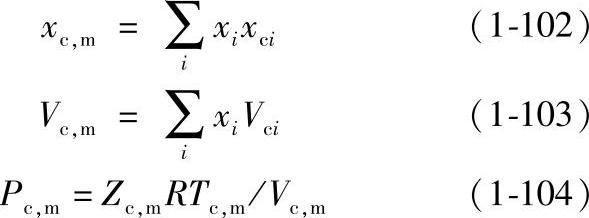
T_c，m、M_m的混合规则与Lucas混合规则相同。

4）液化天然气的粘度计算。液体粘度的理论研究较为复杂，需要多个特性参数，尚难以直接计算液体粘度。一般而言，液体沸点在T^-1_r=1.5K附近。当T^-1_r＜1.5K时，lnη与T^-1_r成线性关系，可由经验公式计算；而沸点以上无此关系，要采用对应态关联式估算。液体混合物的粘度由单组分粘度通过混合规则导出。

液化天然气各组分的粘度可由以下经验公式计算，相应的公式参数见表1-21。

lnη=A+B/T （1-105）

lnη=A+B/T+CT+DT² （1-106）

液化天然气粘度根据各组分的粘度，采用Teja和Rice对应态法计算：

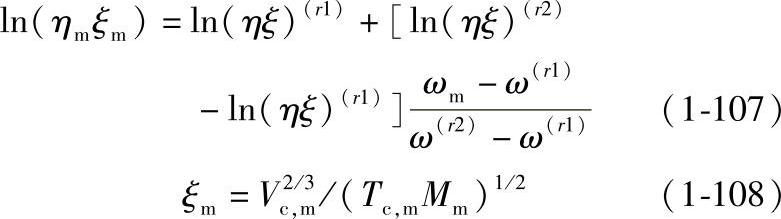
式中，上标（r1）、（r2）代表两种参考流体，可选天然气中摩尔组分最大的两种组分。混合物的参数计算采用式（1-74）至式（1-78）的Teja混合规则。

表1-21 液体粘度的经验公式参数

（4）统一天然气粘度计算模型 上述根据不同压力、相态范围的天然气粘度计算方法在实际应用中显得较为复杂。下面给出一种应用范围广、准确、简洁的天然气粘度计算模型，即基于对应态原理的统一粘度模型，可以对天然气气相和液相粘度进行预测，且计算精度优于Chung模型，Lucas模型和剩余粘度法。

1）对应态原理。以临界点参数为基准，物质的粘度可通过对比参数表示。对比参数定义为实际条件下的参数除以临界点参数。根据对应态原理，如果一组物质中所有物质的对比粘度η_r与对比密度ρ_r和对比温度T_r的函数关系均相同，则该组物质的粘度遵循对应态原理。在这种情况下，仅需要组内一个组分的详细粘度数据，其他组分的粘度以此作为参比就可以很容易地求出。

天然气是以甲烷为主（质量分数为75%以上）的轻烃混合物，各组分的化学性质较为近似，且甲烷拥有大量精确的粘度实验数据。因此，选取甲烷作为参比物质，采用对应态原理可以较好地预测天然气粘度。为校正简单对应态原理与实际混合物粘度计算的偏差，Ely和Hanley提出了形状因子的概念，将对比粘度η_r表示为对比压力p_r和对比温度T_r的函数。由于形状因子的表达式复杂，且需要通过密度的迭代求解确定，致使该算法较为繁琐，并直接影响到粘度计算的精度[2]。为有效解决上述问题，在本文采用的粘度对应态模型中，将η_r表示为对比压力p_r和对比温度T_r的函数：

η_r=ηξ=f（p_r，T_r） （1-109）

式中，ξ是由气体运动理论导出的粘度对比化参数，由下式确定：

ξ=T^1/6_cM^-1/2p^-2/3_c （1-110）

则压力p、温度T状态下混合物的粘度可由下式计算：

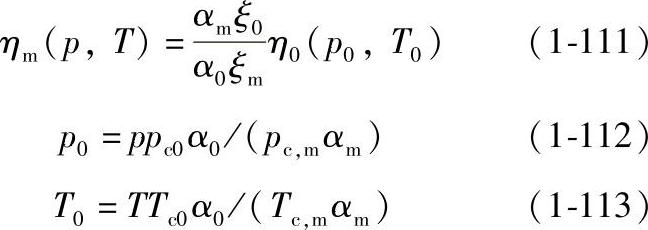
式中，ξ₀、ξ_m是参比物质甲烷和混合物的粘度对比化参数；α_m、α₀是混合物和甲烷的转动耦合系数；η₀是甲烷在压力p₀、温度T₀状态下的粘度。

2）混合规则。根据对应态原理，混合物可看做具有一套按一定规则求出的假临界参数、性质均一的虚拟的纯物质。通过引入混合规则，仅需天然气各组分的摩尔质量、偏心因子和临界参数即可预测混合物粘度。考虑到较重的组分对混合物粘度有较大影响，根据已有的粘度数据可导出如下的混合规则：

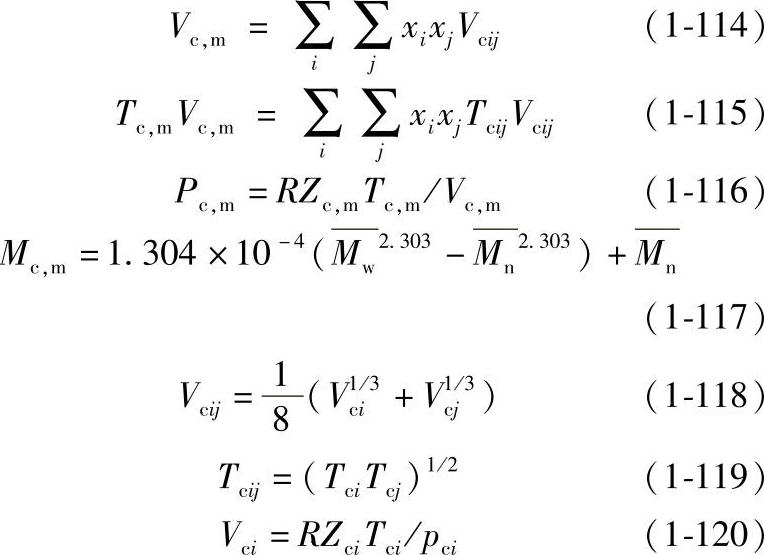
式中，V_c，m、T_c，m、p_c，m、M_c，m是混合物的假临界摩尔体积、假临界温度、假临界压力和临界摩尔质量；x_i、x_j是组分i与j的摩尔分数；M_w、M_n是重量平均摩尔质量与平均摩尔质量。(www.xing528.com)

3）算法

由式（1-111）可计算天然气粘度。天然气和参比物质甲烷的转动耦合系数α_m和α_o可分别由下式估算：

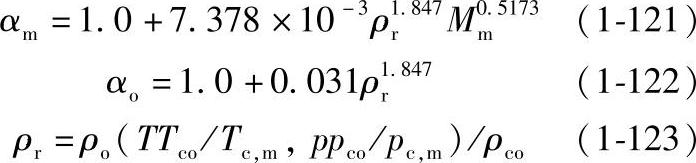
式中，p_co、T_co、ρ_co是参比物质甲烷的临界压力、临界温度和临界密度。

参比物甲烷的粘度计算采用Hanley提出的甲烷粘度模型。该模型建立在大量实验数据的基础上，适用范围广，可用于计算温度95～400K，压力由常压直至50MPa范围的天然气气相和液相粘度误差为2%，具体表达式如下：

η（ρ，T）=η₀（T）+η₁（T）ρ+Δη（ρ，T） （1-124）

式中，ρ是密度；η₀是稀薄气体粘度项；η₁是粘度的密度一阶修正项；Δη是余项。

稀薄气体粘度项η_o可由气体运动理论计算。对于甲烷可采用如下的多项式：

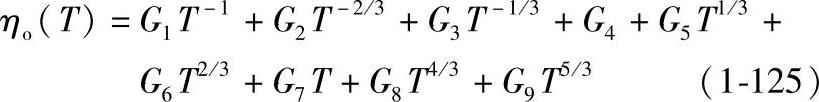
粘度的密度一阶修正项η₁由下式计算：

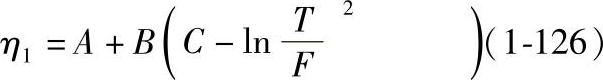
余项Δη由下式计算：

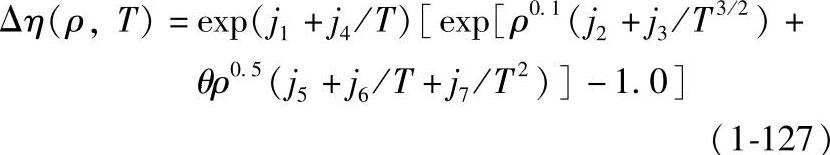
精确求解甲烷密度是粘度计算的关键。甲烷的密度采用McCarty提出的32个参数的甲烷状态方程计算^[6]：

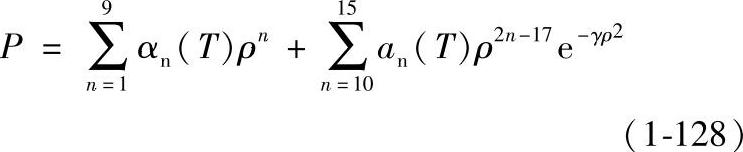
具体参数取值可见参考文献[5]，上述方程采用牛顿法迭代求解。

4）计算结果对比分析。分别采用统一对应态粘度模型、Chung法、Lucas法、剩余粘度法，对三种天然气试样的高压气体粘度进行了预测。其中，剩余粘度法计算中所需要的低压天然气粘度值由Lucas法计算。并采用Anthony^[7]测得的高压天然气粘度数据对不同粘度算法的精度进行验证。详细的计算结果参见文献[8]。通过上述不同算法对高压天然气粘度的预测值与实验数据的比较，得到如下结论：对应态粘度模型的精度最高，平均绝对误差为2.13%；Lu-cas法、剩余粘度法、Chung法的计算精度次之，平均绝对误差分别为2.16%、3.32%和3.82%。

应用对应态粘度模型对二元烃混合物的粘度进行预测，计算结果与Diller测得的甲烷-氮气、甲烷-乙烷和甲烷-丙烷二元烃混合物共计749点的粘度数据进行了比较。结论是，混合物的状态从液相区到稀薄气相区，对应态粘度模型预测结果的平均绝对误差AAD为4.13%。对于液体粘度的预测，对应态粘度模型的平均绝对误差为4.428%，优于Teja和Rice模型6.18%的预测精度。

计算结果表明，对应态粘度模型具有以下优点：该模型将混合物粘度表示为对比压力而不是对比密度的函数，可直接由温度、压力和混合物组成进行计算，简便可行，在高密度区计算误差小。由于参比物质甲烷拥有大量的粘度实验数据和精确的粘度关联式，可充分利用天然气与甲烷性质的相似性预测天然气的迁移性质。大量实验数据与对应态模型的预测结果的比较表明，该模型在宽广的温度和压力范围内对天然气粘度预测具有较高的精度。

2.天然气的热导率

（1）常用热导率计算方法综述 气体热导率常用的计算方法有单原子气体理论方程、Chung热导率模型、Ely-Hanley模型以及Stiel-Thodos模型。高压下气体的热导率随压力变化较为复杂，常用的计算模型有Chung热导率模型、Ely-Hanley模型。Chung热导率模型对非极性气体的平均计算误差为5%～8%，Ely-Hanley模型则较为复杂，对于烃类的计算误差为3%～8%，最大可达15%。气体混合物热导率的计算一般可采用Mason-saxena法、Chung法、Stiel-Tho-dos模型计算。

液体的热导率测定由于液体对流的存在而非常困难，实验数据更显缺乏。目前理论研究虽然很多，但尚难以直接预测热导率，一般还是采用估算法。液体热导率较为重要的几种计算方法为Sato-Reidel法、Latini法、Sheffy-Johnson法、Jamieson双参数方程。相比较而言，Jamieson双参数方程适用的物质类别和温度范围较广。总的来说，液体热导率的计算还是以采用经验关联式较为准确。由于实验数据的缺乏，多元液体混合物热导率的研究还很不成熟。目前，液体混合物热导率的估算方法有指数方程、Li方程等。

（2）不同压力范围及相态的天然气的热导率计算模型 热导率的理论研究较为复杂，需针对物质所处的不同状态选择合适的计算模型。

1）低压天然气的热导率计算。精度较高的可直接对混合物热导率进行计算的模型有Chung热导率模型，另外若已知混合物各组分的热导率值，也可采用Mason-Saxenafa法计算混合物热导率。

①Chung热导率模型。采用式（1-60）至式（1-73）的Chung混合规则，低压气体热导率的计算公式为

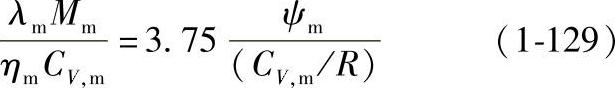
式中，λ_m是混合物热导率；M_m是混合物摩尔质量；η_m是气体混合物粘度；ψ_m是校正系数。C_V，m是混合物摩尔定容热容，由下式计算：

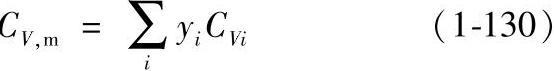
②Mason-Saxenafa法。将混合物的热导率表示为不同组分热导率的关系式：

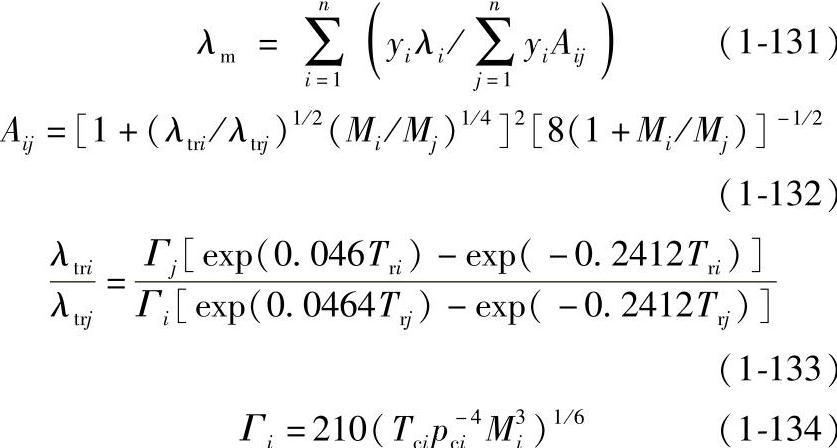
式中，λ_tri、λ_trj是组分i和j的单原子热导率；Γ_i、Γ_j是组分i和j的对比热导率的倒数。

Mason-Saxenafa算法在已知混合物各组分热导率的情况下，对非极性低压气体混合物的计算误差为3%～4%。当混合物各组分热导率未知时，必须通过其他的纯物质热导率模型计算各组分热导率。Stiel-Thodos模型是单组分热导率模型中精度较高的一种，计算公式如下：

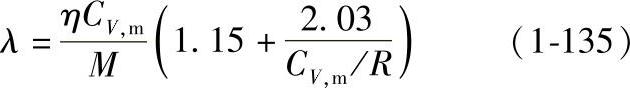
2）高压天然气的热导率计算。当压力在10^-4～1MPa时，压力对气体热导率的影响可忽略不计。高于1MPa时，气体热导率随压力的变化关系比较复杂。高压天然气热导率计算可采用Chung热导率模型和Stiel-Thodos模型。

①考虑压力的影响，Chung高压气体热导率的计算公式为

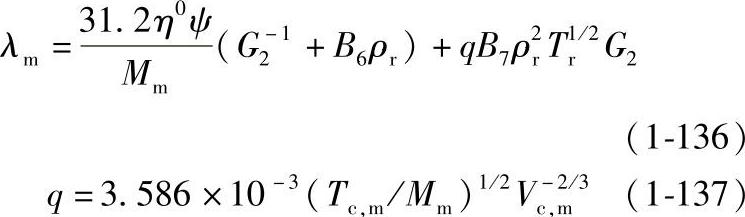
式中，ρ_r是对比密度；η⁰是低压气体粘度；G₂是校正因子。

Chung法将压力修正项定义为气体密度的函数，需要计算混合物密度。

②Stiel-Thodos高压热导率模型的具体表达式如下：

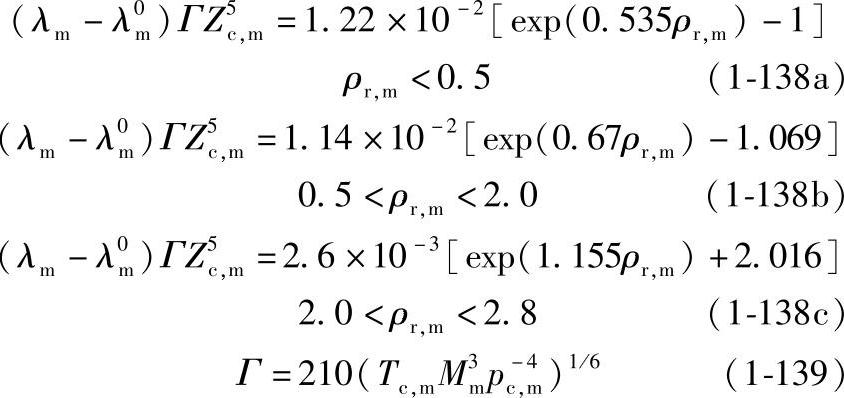
式中，λ_m是高压气体混合物热导率；λ⁰_m是低压气体混合物热导率；ρ_r，m是混合物虚拟对比密度；Z_c，m是混合物的虚拟临界压缩因子。

Stiel-Thodos模型的混合规则与Teja对应态相同。

3）液化天然气的热导率计算。大多数液体的热导率随温度升高而减少，但不像粘度那样对温度敏感。在沸点前，热导率与温度近似成直线关系。常温下，压力对液体的影响较小。直至5～6MPa的中压范围，工程上仍可忽略压力对热导率的影响。液体混合物的热导率一般由单组分热导率通过混合规则导出。目前较为成熟的混合物热导率模型大多针对二组分混合物，多组分液体混合物的热导率公式相对较少，以Li模型较为方便、准确。本节液化天然气的热导率计算采用热导率经验关联式与Li模型结合使用的方法。

液化天然气各组分的热导率可由以下经验公式计算，有机物采用式（1-140），无机物采用式（1-141），相应的公式参数见表1-22。

lgλ=A+B[1-T/C]^2/7 （1-140）

λ=A+BT+CT² （1-141）

表1-22 液化天然气组分液体热导率的经验公式参数

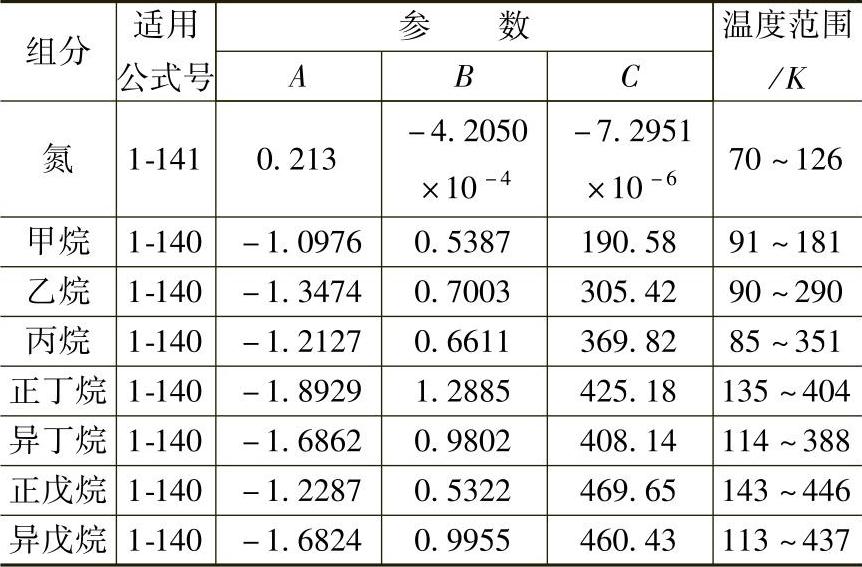
Li模型如下：

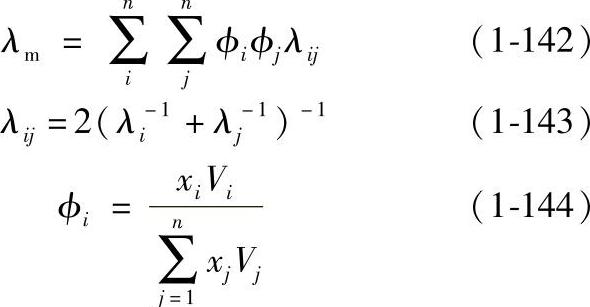
式中，x_i是组分i的摩尔分数；ϕ_i是组分i的体积分数；V_i是组分i纯液体的摩尔体积。

（3）天然气的热导率对应态预测模型 同前面对天然气粘度算法的计算分析可知，采用对应态模型预测天然气粘度具有适用范围广、精度高的优点，这主要是由于参比物质甲烷和天然气的化学结构和相对分子质量近似相同，较好地符合了对应态原理。因此，这里也采用对应态理论计算天然气热导率。

1）对应态原理。简单热导率对应态模型中，对于一组遵循对应态原理的物质，对比热导率可以表示为对比压力ρ_r和对比温度T_r的函数：

λ_r=λξ=f（p_r，T_r） （1-145）

式中，ξ是由气体运动理论导出的热导率对比化参数，由下式确定：

ξ=T^1/6_cM^1/2p_c^-2/3 （1-146）

混合物的热导率计算必须对简单的对应态原理进行校正。将热导率分成两部分：

λ=λ_tr+λ_int （1-147）

式中，λ_tr是平移能量传递对热导率的贡献；λ_int是内能传递对热导率的贡献。

对应态理论只适用于计算混合物热导率中的平移项。

采用校正系数α校正混合物热导率与简单对应态模型之间的偏离，得到如下的混合物热导率的模型^[10]：

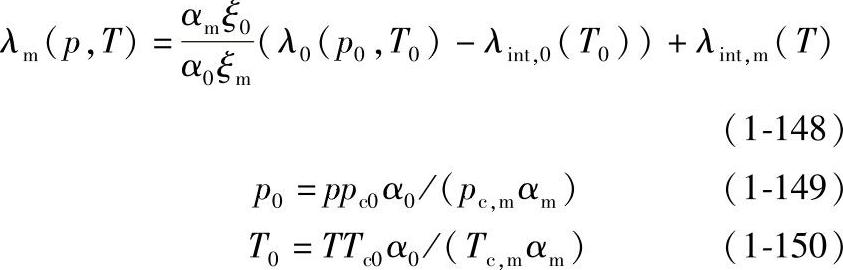
式中，ξ₀、ξ_m是混合物和参比物质的热导率对比化参数；α_m、α₀是混合物和参比物质的热导率校正项；λ₀是参比物质在压力p₀、温度T₀状态下的热导率；λ_int，0、λint，m是参比物和混合物热导率的内能项。

λ_int=1.18653η₁（c_p^id-2.5R）f（ρ_r）/M （1-151）

f（ρ_r）=1+0.053432ρ_r-0.03182ρ²_r-0.029725ρ³_r （1-152）

式中，η₁是混合工质在温度T和101kPa下的粘度；c^id_p是温度T时理想气体的比定压热容。

2）混合规则。热导率的混合规则与天然气粘度对应态模型类似，T_c，m，p_c，m可分别由式（1-114）至式（1-120）计算，混合物的相对分子质量M_m由Chap-man-Enskog理论导出：

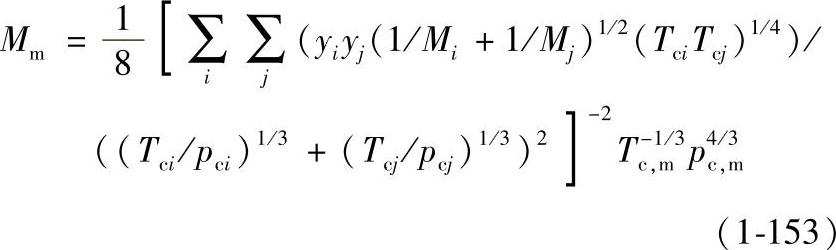
3）算法。由式（1-148）即可根据甲烷的热导率计算天然气的热导率混合物的热导率校正项α_m由下式估算：

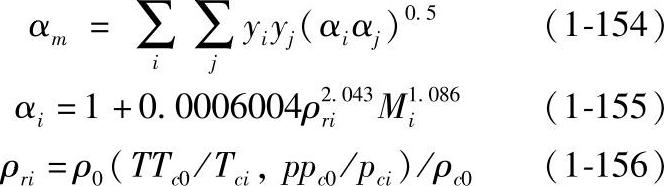
本文采用Hanley提出的甲烷热导率模型，该模型建立在大量实验数据的基础上，适用范围广，可用于计算温度95～400K，压力由常压直至50MPa范围内的甲烷气态、液态的热导率，最大误差为2%。甲烷热导率模型的具体表达式如下：

λ（ρ，T）=λ₀（T）+λ₁（T）ρ+Δλ（ρ，T）+Δλ_c（ρ，T） （1-157）

式中，ρ是密度；λ₀是稀薄气体热导率；λ₁是热导率的密度一阶修正项；Δλ是余项；Δλ_c是热导率的临界点增强项。

4）计算结果对比分析。采用对应态热导率模型、Chung法和Stiel-Thodos模型对二元混合物气体的热导率进行了预测。预测结果与Christensen测得的甲烷-氮气、甲烷-二氧化碳进行了对比。从预测结果可知：对应态热导率模型的平均绝对误差为5.03%；Chung法、Stiel-Thodos模型的平均绝对误差分别为4.93%和7.57%。

采用上述热导率模型对一组氮烃类混合物的热导率进行了预测，混合物组分的摩尔分数为：N₂（0.367），CH₄（0.246），C₂H₆（0.12），C₃H₈（0.267）。对应态热导率模型对混合物气相预测的平均绝对误差为2.09%，Chung法、Stiel-Thodos模型的平均绝对误差分别为2.35%和4.38%。对应态热导率模型对混合物液相的平均绝对误差为4.35%，而Li模型的计算平均绝对误差为7.51%。

由上述计算结果可知，对应态热导率模型、Chung法的计算精度要优于Stiel-Thodos模型。而且对应态热导率模型的适用温度、压力范围广，精度较高，优点较为明显。