1.对流换热的理论基础
在工程实践中,存在大量的对流换热实例,如换热器管内流动沸腾换热等。流体流过固体表面所发生的热量交换称为对流换热。
(1)牛顿冷却公式及影响对流换热的因素 对流换热是指流体流经固体时流体与固体表面之间的热量传递现象。对流换热的基本计算公式是牛顿冷却公式,即热流密度q=hΔt,其中,h是表面传热系数;对于面积为A的接触面,则对流换热量Φ=hAΔtm。其中,Δtm为换热面与流经该面流体的平均温差。约定q和Φ总是取正值,Δt和Δtm也总是取正值。
对流换热是流体的导热和对流两种基本传热方式共同作用的结果。影响对流换热的因素是影响流动的因素和影响流体中热量传递的因素综合作用,基本有以下五个因素:
1)流体流动的起因。按照流动起因的不同,对流换热分为强制对流换热和自然对流换热两大类。前者是由于泵、风机或其他外部动力源造成的;后者是由于流体内部的密度差所引起。两种流动流体中的速度场有差别,换热规律不一样。
2)流体有无相变。在流体没有相变时,对流换热中的热量交换是由于流体的显热变化而实现的,而在有相变的换热过程中(如沸腾或凝结时),流体的相变潜热往往起着主要作用,因而换热规律与无相变时不同。
3)流体的流动(单相流动)状态。粘性流体在层流时,流体微团沿着主流方向作有规则的分层流动;而湍流时,流体各部分之间发生剧烈的混合。因此,在其他条件相同时两种流态的换热能力不相同。
4)流体的物理性质。流体的物理性质,如流体密度、动力粘度、热导率等对流体的流动和流体中的热量传递都有影响。
5)换热表面的几何因素。换热表面的形状、大小、换热表面与流体运动方向不同的流动条件,对换热的影响是不同。
(2)相似原理与对流换热问题的无量纲准则方程式的建立 通过实验求取对流换热的实验关联式,是传热学解决问题的重要手段。但对于存在着许多影响因素的复杂物理现象,要找出众多变量间的函数关系,实验次数十分庞大。为了减少实验次数,得出具有一定通用性的结果,必须在相似原理的指导下进行实验。
1)相似。同类的物理现象,在相应的时刻与相应的地点上,与现象有关的物理量一一对应成比例,即为彼此相似。相似的概念只限于在同类的物理现象之间,即指用相同形式并具有相同内容的微分方程式所描写的现象。两个彼此相似的稳态对流换热现象,必须具备几何形状相似、温度场分布相似、速度场分布相似及热物性场相似等。凡是相似的物理现象,其物理量的场一定可以用一个统一的量纲为1的场来表示。
2)判断两个同类现象相似的条件。相似原理规定物理现象相似所必须满足的条件。
①同名的已定特征数相等。已定特征数是由所研究问题的已知量组成的特征数。
②单值性条件相似。包括初始条件、边界条件、几何条件和物理条件。
3)物理量量纲为1化和特征数方程。物理量量纲为1化,是通过确定某一特征尺度,使物理量量纲为1。表示物理现象解的量纲为1的物理量之间的函数关系式,称为特征数方程。
4)相似分析法。此法是根据相似现象的基本定义——各个物理量的场对应成比例,对于过程有关的量引入两个现象之间的一系列比例系数(称相似倍数),然后应用描述该过程的一些数学关系式,导出制约这些相似倍数间的关系,从而得出相应的相似特征数。
①雷诺数Re。若流体的两个运动现象相似,则Re′=Re″,其中Re为表示流动相似的量纲为1的数,且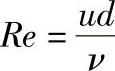 。
。
①雷诺数Re。若流体的两个运动现象相似,则Re′=Re″,其中Re为表示流动相似的量纲为1的数,且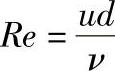 。
。
②贝克来数Pe。如两热量传递现象相似,则有Pe′=Pe″,其中Pe表示热量传递现象相似的量纲为1的数,且P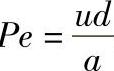 。
。
②贝克来数Pe。如两热量传递现象相似,则有Pe′=Pe″,其中Pe表示热量传递现象相似的量纲为1的数,且P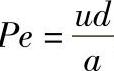 。
。
③普朗特数Pr。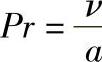 也是一个量纲为1的数,表示动量扩散厚度与热量扩散厚度之比的一种度量。
也是一个量纲为1的数,表示动量扩散厚度与热量扩散厚度之比的一种度量。
④努塞尔数Nu。图1-12示出流体与固体间的对流换热现象,有
③普朗特数Pr。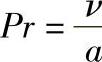 也是一个量纲为1的数,表示动量扩散厚度与热量扩散厚度之比的一种度量。
也是一个量纲为1的数,表示动量扩散厚度与热量扩散厚度之比的一种度量。
④努塞尔数Nu。图1-12示出流体与固体间的对流换热现象,有
由相似现象定义导得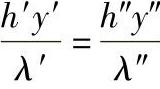
即Nu′=Nu″
由相似现象定义导得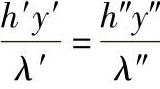
即Nu′=Nu″
式中,Nu为量纲为1的数,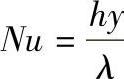 (y是边界层厚
(y是边界层厚
度)。
式中,Nu为量纲为1的数,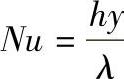 (y是边界层厚
(y是边界层厚
度)。
图1-12 流体中的温度分布
⑤格拉晓夫数Gr。此特征数表明自然对流中浮升力的影响,是浮升力与粘性力之比的一种量度。
图1-12 流体中的温度分布
⑤格拉晓夫数Gr。此特征数表明自然对流中浮升力的影响,是浮升力与粘性力之比的一种量度。
式中,αV是流体的体胀系数;l是特征长度。(https://www.xing528.com)
应用相似原理可指导试验的安排及试验数据的处理,并将结果整理成准则数间的关系式,但具体的函数形式以及定性温度和特征长度的确定,则带有经验的性质。
2.对流换热问题
(1)自然对流换热 不依靠泵或风机等外力推动,由流体自身温度场的不均匀所引起的流动称为自然对流。
自然对流分为层流和湍流。图1-13为贴近热竖壁的自然对流情况。在壁的下部,流动刚开始形成,它是有规则的层流;若壁面足够高,则上部流动会转变为湍流。不同的流动状态对换热具有决定性的影响。层流时,换热热阻主要取决于薄层的厚度。从换热壁面下端开始,随着高度的增加,层流薄层的厚度也逐渐增加。图中的曲线表示换热系数hx沿竖壁高度x的变化。可见,hx随高度增加而减小。如果壁面高度足够,流体的流动将逐渐转变为湍流。湍流时换热规律有所变化。旺盛湍流时,局部表面换热系数hx几乎是常量。
式中,αV是流体的体胀系数;l是特征长度。
应用相似原理可指导试验的安排及试验数据的处理,并将结果整理成准则数间的关系式,但具体的函数形式以及定性温度和特征长度的确定,则带有经验的性质。
2.对流换热问题
(1)自然对流换热 不依靠泵或风机等外力推动,由流体自身温度场的不均匀所引起的流动称为自然对流。
自然对流分为层流和湍流。图1-13为贴近热竖壁的自然对流情况。在壁的下部,流动刚开始形成,它是有规则的层流;若壁面足够高,则上部流动会转变为湍流。不同的流动状态对换热具有决定性的影响。层流时,换热热阻主要取决于薄层的厚度。从换热壁面下端开始,随着高度的增加,层流薄层的厚度也逐渐增加。图中的曲线表示换热系数hx沿竖壁高度x的变化。可见,hx随高度增加而减小。如果壁面高度足够,流体的流动将逐渐转变为湍流。湍流时换热规律有所变化。旺盛湍流时,局部表面换热系数hx几乎是常量。
图1-13 贴近热竖壁的自然对流情况
自然对流换热分为大空间和有限空间两类。在大空间自然对流换热情况下,流体的冷却和加热过程互不影响。
(2)强制对流换热 影响强制对流换热的主要因素有:
1)层流和湍流流动形态的影响。当Re<2300时,流动为层流;当2300<Re<10000时,流动处于过渡区内;当10000<Re时,流动为旺盛湍流。
2)入口段的影响。入口段的热边界层薄,表面传热系数高。层流入口段的l/d≈0.05RePr;湍流入口段的l/d≈60。图1-14为层流、湍流入口段示意图。
3)热边界条件的影响。热边界条件指均匀壁温和均匀热流。除液态金属外,湍流对两种条件的差别可不计;层流的两种边界条件下的换热系数差别明显。图1-15示出流体温度和壁面温度沿主流方向的变化。
图1-13 贴近热竖壁的自然对流情况
自然对流换热分为大空间和有限空间两类。在大空间自然对流换热情况下,流体的冷却和加热过程互不影响。
(2)强制对流换热 影响强制对流换热的主要因素有:
1)层流和湍流流动形态的影响。当Re<2300时,流动为层流;当2300<Re<10000时,流动处于过渡区内;当10000<Re时,流动为旺盛湍流。
2)入口段的影响。入口段的热边界层薄,表面传热系数高。层流入口段的l/d≈0.05RePr;湍流入口段的l/d≈60。图1-14为层流、湍流入口段示意图。
3)热边界条件的影响。热边界条件指均匀壁温和均匀热流。除液态金属外,湍流对两种条件的差别可不计;层流的两种边界条件下的换热系数差别明显。图1-15示出流体温度和壁面温度沿主流方向的变化。
图1-14 层流、湍流入口段示意图
图1-14 层流、湍流入口段示意图
图1-15 流体温度及壁面温度沿主流方向的变化
a)均匀热流密度 b)均匀壁温
4)特征速度及定性温度的确定。特征速度一般多取截面平均流速。定性温度多为截面上流体的平均温度,或进出口截面平均温度。
5)牛顿冷却公式中的平均温差。对恒热流条件,可取(tw-tf)作为Δtm。此时有
hmAΔtm=qmcp(tf″-tf′)
图1-15 流体温度及壁面温度沿主流方向的变化
a)均匀热流密度 b)均匀壁温
4)特征速度及定性温度的确定。特征速度一般多取截面平均流速。定性温度多为截面上流体的平均温度,或进出口截面平均温度。
5)牛顿冷却公式中的平均温差。对恒热流条件,可取(tw-tf)作为Δtm。此时有
hmAΔtm=qmcp(tf″-tf′)
式中,qm是质量流量;tf″、tf′是出口、进口截面上的平均温度;Δtm是对数平均温差,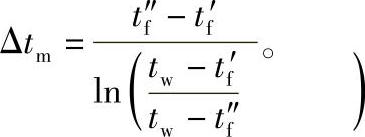
式中,qm是质量流量;tf″、tf′是出口、进口截面上的平均温度;Δtm是对数平均温差,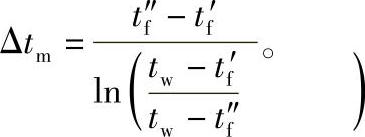
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




