理想流体运动的基本方程：流体动力学基础

1.理想流体运动的分类

1）若运动参数与时间无关，则称此流动为定常流动；反之，称为非定常流动。定常流动的流场中速度

u=u（x，y，z），v=v（x，y，z），w=w（x，y，z） （1-42）

压力和密度表示为

p=p（x，y，z），ρ=ρ（x，y，z） （1-43）

2）按照流场空间自变量数，可将流体流动分为一维、二维或三维流动。

2.连续性方程

流体在流动过程中应该遵循质量守恒定律，且不违背连续介质假设，连续性方程就是流体上述性质的数学表达形式。

对于不可压缩流体，ρ是常数，连续性方程简化为

式（1-44）表明六面表面净流入的体积流量为零。

对于一元管流定常流动，引用平均速度，则得连续性方程为

v₁A₁=v₂A₂ （1-45）

式中，v₁、v₂是有效断面A₁，A₂上的平均速度。

3.理想流体的伯努利方程

（1）伯努利方程 在上述条件下，且质量力仅仅是重力，即f_x=0，f_y=0，f_z=-g，势函数π=gz；流体是不可压缩的，可得出伯努利方程为

式（1-44）表明六面表面净流入的体积流量为零。

对于一元管流定常流动，引用平均速度，则得连续性方程为

v₁A₁=v₂A₂ （1-45）

式中，v₁、v₂是有效断面A₁，A₂上的平均速度。

3.理想流体的伯努利方程

（1）伯努利方程 在上述条件下，且质量力仅仅是重力，即f_x=0，f_y=0，f_z=-g，势函数π=gz；流体是不可压缩的，可得出伯努利方程为

使用伯努利方程时应满足下列条件：①流体必须是理想的、不可压缩的；②流动必须是定常的；③质量力仅仅是重力：④在流动无旋时，它在整个流场上成立；在流动有旋时，它仅沿流线成立。

使用伯努利方程时应满足下列条件：①流体必须是理想的、不可压缩的；②流动必须是定常的；③质量力仅仅是重力：④在流动无旋时，它在整个流场上成立；在流动有旋时，它仅沿流线成立。

1)伯努利方程的物理意义。从物理角度看，式(l-46a)中第一项zg表示单位质量流体所具有的位势能：第二项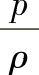表示单位质量流体所具有的压力势能：第三项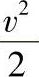表示单位质量流体所具有的动能。以三种能量之和称为总机械能。这表明：在整个流场中沿流线，单位质量流体所具有的位势能、压力势能、动能之和是常数，或者说，总机械能是常数。

1)伯努利方程的物理意义。从物理角度看，式(l-46a)中第一项zg表示单位质量流体所具有的位势能：第二项表示单位质量流体所具有的压力势能：第三项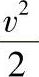表示单位质量流体所具有的动能。以三种能量之和称为总机械能。这表明：在整个流场中沿流线，单位质量流体所具有的位势能、压力势能、动能之和是常数，或者说，总机械能是常数。

2）伯努利方程的几何意义。从几何角度看，式（1-46b）的第一项z表示位置水头；第二项表示压力水头；第三项表示速度水头。三种水头之和称为总水头，前两种水头之和称为测压管水头。这表明：在整个流场中沿流线，任意点的位置水头、压力水头和速度水头之和是常数。如果把基准面作为起点，画出每一点的总水头，则所有水头高度线的端点应落在同一水平线上，这条水平线称为总水头线。各点测压管水头的连线称为测压管水头线，如图1-8所示。

2）伯努利方程的几何意义。从几何角度看，式（1-46b）的第一项z表示位置水头；第二项表示压力水头；第三项表示速度水头。三种水头之和称为总水头，前两种水头之和称为测压管水头。这表明：在整个流场中沿流线，任意点的位置水头、压力水头和速度水头之和是常数。如果把基准面作为起点，画出每一点的总水头，则所有水头高度线的端点应落在同一水平线上，这条水平线称为总水头线。各点测压管水头的连线称为测压管水头线，如图1-8所示。

图1-8 伯努利方程的几何意义图示

忽略重量的影响伯努利方程可简化为

图1-8 伯努利方程的几何意义图示

忽略重量的影响伯努利方程可简化为(www.xing528.com)

即不考虑重力影响，在流体内压力低的地方速度大，压力高的地方速度小。

（2）总流的伯努利方程 沿流线的伯努利方程用到总流上，需要一定的限制条件和进行必要的修正。

即不考虑重力影响，在流体内压力低的地方速度大，压力高的地方速度小。

（2）总流的伯努利方程 沿流线的伯努利方程用到总流上，需要一定的限制条件和进行必要的修正。

图1-9为急变流和缓变流示意图。流线几乎是平行的直线的流动称为缓变流，不符合上述条件的流动称为急变流。缓变流的主要特点是：沿有效断面，。

图1-10为总流中任一微主流束示意图。单位时间内通过总流有效断面A₁和A₁的能量之间的关系式为

图1-9为急变流和缓变流示意图。流线几乎是平行的直线的流动称为缓变流，不符合上述条件的流动称为急变流。缓变流的主要特点是：沿有效断面，。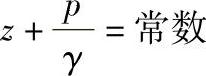

图1-10为总流中任一微主流束示意图。单位时间内通过总流有效断面A₁和A₁的能量之间的关系式为

假设A₁，A₂都处在缓变流中，则有

假设A₁，A₂都处在缓变流中，则有

用平均速度v₁，v₂表示通过A₁和A₂的流体所具有的动能，并考虑到有效断面上速度分布的布均匀性，引入动能修正系数α：，在工业管道通常的工作状态下α=1.05～1.12，一般可近似地取α=1，则

用平均速度v₁，v₂表示通过A₁和A₂的流体所具有的动能，并考虑到有效断面上速度分布的布均匀性，引入动能修正系数α：，在工业管道通常的工作状态下α=1.05～1.12，一般可近似地取α=1，则

用v₁和v₂代表平均速度，则总流的伯努利方程为

用v₁和v₂代表平均速度，则总流的伯努利方程为

如果取α₁=α₂=1，则有广泛应用得总流伯努利方程

如果取α₁=α₂=1，则有广泛应用得总流伯努利方程

图1-9 急变流和缓变流示意图

图1-9 急变流和缓变流示意图

图1-10 总流中任一微元流束示意图

总流伯努利方程应用的条件如下：

1）流体是理想、不可压缩的；流动是定常的；质量力仅仅是重力。

2）所取的两个有效断面一定要处于缓变流区域，但在这两个有效断面之间可以有急变流。

3）在所取的两个有效断面之间不能有能量输入或输出。

图1-10 总流中任一微元流束示意图

总流伯努利方程应用的条件如下：

1）流体是理想、不可压缩的；流动是定常的；质量力仅仅是重力。

2）所取的两个有效断面一定要处于缓变流区域，但在这两个有效断面之间可以有急变流。

3）在所取的两个有效断面之间不能有能量输入或输出。

4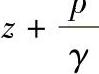）在缓变流的同一有效断面上是常数，因此可以在断面上任意点取值，一般取断面形心处的值较方便。

4）在缓变流的同一有效断面上是常数，因此可以在断面上任意点取值，一般取断面形心处的值较方便。