流体静力学基础：流体平衡

如果流体相对于某一坐标系静止不动，即流体在力学上处于平衡状态。流体在平衡状态下的力学规律称为流体静力学。所谓流体静止状态，是指所有的流体质点相对于某一选定的坐标系没有运动。通常把地球选择为惯性参考坐标系，若所选参考坐标系相对于地球表面没有运动，在该坐标系下的静止为绝对静止（简称静止）；若所选参考坐标系相对于地球表面有运动，在该坐标系下的静止为相对静止。

流体处于静止或相对静止状态时所具有的共性是：由于流体质点间没有相对运动，流体不呈现粘性，流体内每一点的切应力都为零。作用在静止流体的表面力只有静压力，此时在外力作用下，流体处于平衡的力学规律就是压力（压强）分布规律。

1.平衡状态下流体中的应力特征

当流体处于静止或相对静止状态时，作用在流体上的静压力就是负的法向应力。具有两个重要特征：

1）流体静压力的方向垂直于作用面，并沿作用面的内法线方向。

2）流体静压力的大小与作用面的方向无关，只是该点坐标的函数。即在静止流体中的任意给定点上，不论来自何方的静压力均相等。

2.流体静力学基本方程

作用在流体上的质量力仅仅是重力，而流体又近似为均质不可压缩的（ρ=常数）。流体静力学基本方程适用在重力场中处于静止状态的均质不可压缩流体。

p=p₀+γh （1-36）

这就是压力传递的帕斯卡原理（Blaise Pascal）。

3.压力

压力可以用绝对压力、表压力和真空度来表示。以完全真空为基准计量的压力称为绝对压力；以大气压力为基准的压力称为表压力。绝对压力p与表压力p_g和大气压力p_a之间的关系为p_g=p-p_a。

当流体处于真空状态时，表压力的大小通常用真空度p_v来表示。真空度与绝对压力、大气压力和表压力之间的关系为p_v=p_a-p=-p_g。

4.作用在物体表面的液体总压力

工程上在设计各种阀、容器、管道、水工建筑物时，不仅要知道流体中压力的分布，而且还需求得浸没在静止液体中的物体表面所受总压力的大小及其作用点。

（1）均质流体作用在平面上的液体总压力 图1-7所示一个浸没在静止流体中的平面与水平面之间的交角为α，它的面积为A。取坐标系如图所示，x轴和y轴在平面上，z轴垂直于平面。平面上各点的淹深不一样，故各点的压力亦不相同。压力都沿法向指向平壁，故流体合力的方向显然垂直于平壁并指向内侧。作用在整个面积A上的总压力p_t为

由于h=ysina

由于h=ysina

所以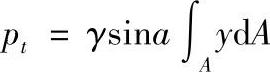

积分∫_AydA是面积A对OX轴的静面矩，如果面积A的形心C点的y坐标为y_c，则

所以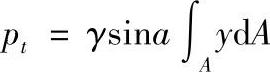

积分∫_AydA是面积A对OX轴的静面矩，如果面积A的形心C点的y坐标为y_c，则(www.xing528.com)

因此 p_t=γy_csinaA=γh_cA （1-37）

式中，h_c是形心点C的淹深，h_c=y_csina。

静止液体作用在平面上的总压力，等于平面形心点处的表压力γh_c与平面面积A的乘积。

因此 p_t=γy_csinaA=γh_cA （1-37）

式中，h_c是形心点C的淹深，h_c=y_csina。

静止液体作用在平面上的总压力，等于平面形心点处的表压力γh_c与平面面积A的乘积。

图1-7 平面上所受均质流体的作用示意图

总压力的作用点压力中心，根据理论力学中“平行力系中的诸力对某轴的力矩之和等于合力对该轴的力矩”可得

图1-7 平面上所受均质流体的作用示意图

总压力的作用点压力中心，根据理论力学中“平行力系中的诸力对某轴的力矩之和等于合力对该轴的力矩”可得

y_D是压力中心D的y坐标。dp_t=γysinadA；p_t=γy_csinaA

y_D是压力中心D的y坐标。dp_t=γysinadA；p_t=γy_csinaA

则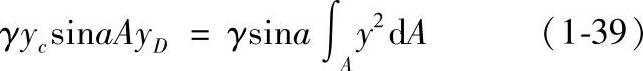

式中，∫_Ay²dA为面积A对OX轴的惯性矩，用J_x表示，故式（1-39）可整理成

则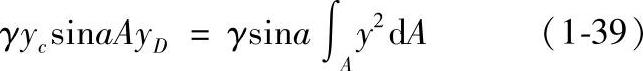

式中，∫_Ay²dA为面积A对OX轴的惯性矩，用J_x表示，故式（1-39）可整理成

根据惯性矩的平行转移轴公式J_x=J_c+y²_cA，得到压力中心的坐标y_D为

根据惯性矩的平行转移轴公式J_x=J_c+y²_cA，得到压力中心的坐标y_D为

压力中心D总是位于形心点C的下方。

压力中心D总是位于形心点C的下方。