1.热力学
自然界中可供大量产生动力的主要能源有风能、水能、太阳能、地热能、燃料化学能、原子能等。目前利用得最多的仍然是矿物燃料（石油、煤、天然气等）的化学能。各种能源除风能（空气的动能）和水能（水的位能）可以向人们直接提供机械能以外，其他各种能源往往只能直接或间接地（通过燃烧、核反应）提供热能。大量的要通过热机（如蒸汽轮机、内燃机、燃气轮机、喷气发动机等）使这些热能部分地转变为机械能，或进一步转变为电能，以供人类生产和生活的需求。掌握热能性质及其转换规律具有重要实用价值和理论意义。
2.热机和工质
热机是将热能转变为机械能的机械设备，载能物质便是工质。热机对外做功时，要求工质有良好的膨胀性和良好的流动性，才能实现持续不断地做功。由于气体同时具备良好的膨胀性和流动性，热机中的工质一般是气态物质。
3.热力学与工程热力学
工程热力学着眼于根据热力学的两个基本定律，运用严密的逻辑推理，对物体的宏观性质和宏观现象进行分析研究，并利用所获的定律、结果和公式进行工程设计和计算。
热力学除了宏观研究理论外，还有微观理论研究，即根据热学的微观理论——统计物理学，从物质的微观结构出发，依据微观粒子的力学规律，应用概率理论和统计平均的方法，研究大量微观粒子（它们构成宏观物体）的运动表现出来的宏观性质。
4.工程热力学常用的计量单位
国际单位制是我国法定计量单位的基础，一切属于国际单位制的单位都是我国法定计量单位。工程热力学中各常用物理量牵涉到的基本单位有5个，即长度、质量、时间、热力学温度和物质的量。
表1-1和表1-2列出工程热力学中常用的国家法定计量单位的基本单位和导出单位。
表1-1 国家法定计量单位的基本单位
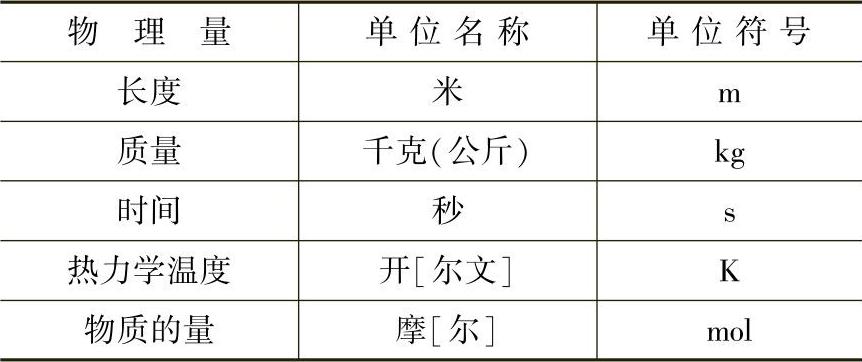
表1-2 国家法定计量单位的导出单位（部分）
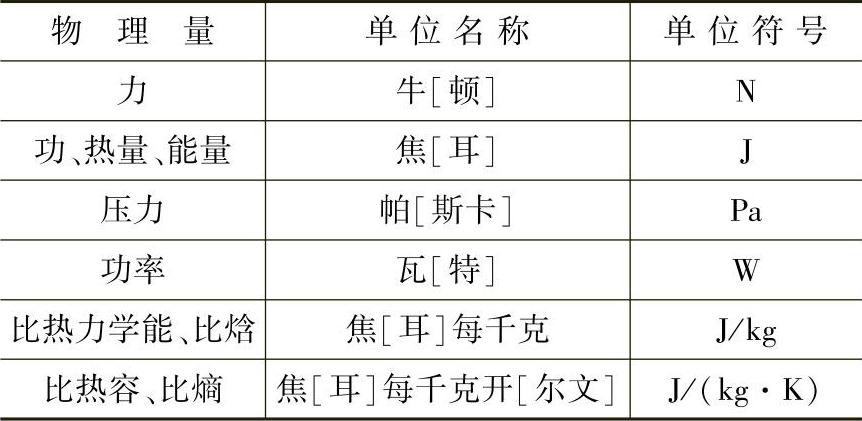
5.热力系
热力系就是具体指定的热力学研究对象。与热力系有相互作用的周围物体通称为外界。为了避免把热力系和外界混淆起来，设想有界面将它们分开。
在作热力学分析时，既要考虑热力系内部的变化，也要考虑热力系通过界面和外界发生的能量交换和物质交换，而外界的变化，一般不予考虑。
根据热力系内部情况的不同，热力系可以分为：①单元系——由单一的化学成分组成；②多元系——由多种化学成分组成；③单相系——由单一的相（如气相或液相）组成；④复相系——由多种相（如气-液两相或气-液-固三相等）组成；⑤均匀系——各部分性质均匀一致；⑥非均匀系——各部分性质不均匀。
根据热力系和外界相互作用情况的不同，热力系又可以分为：①闭口系——和外界无物质交换；②开口系——和外界有物质交换；③绝热系——和外界无热量交换；④孤立系——和外界无任何相互作用。
6.状态和状态参数
状态是热力系在指定瞬间所呈现的全部宏观性质的总称。从各个不同方面描写这种宏观状态的物理量便是各个状态参数。
在工程热力学中常用的状态参数有6个，即压力、比体积、温度、热力学能、焓和熵。其中压力、比体积和温度可以直接测量比较直观，称为基本状态参数。
（1）压力 指单位面积上承受的垂直作用力：
式中，p是压力（Pa）；F是垂直作用力（N）；A是面积（m2）。
气体的压力是组成气体的大量分子在紊乱的热运动中对容积壁频繁碰撞的结果。
1）绝对压力：式（1-1）所定义的压力是气体的真正压力，称为绝对压力。
2）表压力：由测量压力的仪表在大气环境中所得到的读数。读数为正（负）称为表压力（真空度）。
法定单位制中，压力的单位是Pa（帕）。表1-3列出常见非法定压力单位的换算关系。
表1-3 常见非法定压力单位的换算关系
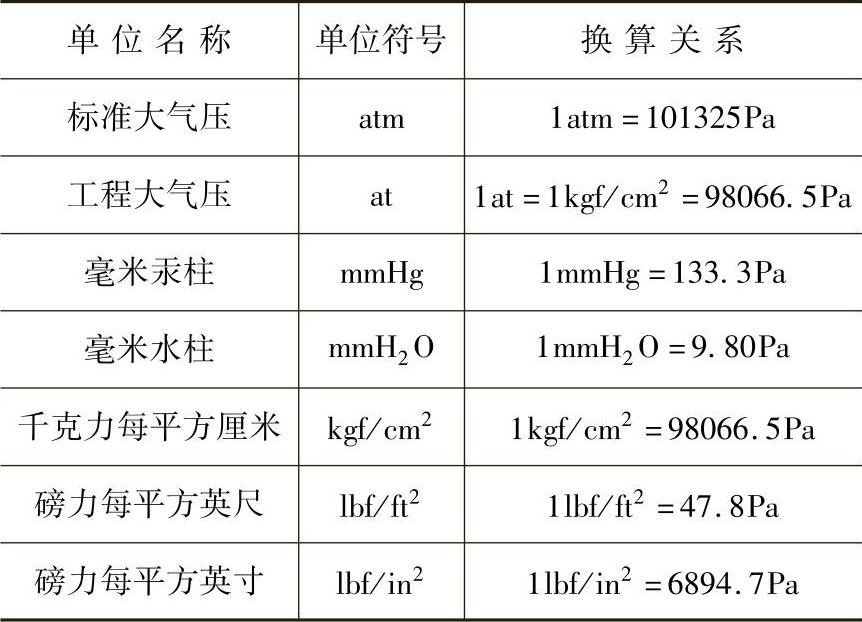
（2）比体积 比体积就是单位质量的物质所占有的体积，即
式中，v是比体积（kg/m3）；V是体积（m3）；m是质量（kg）。
比体积的倒数就是密度（ρ）。密度是单位体积的物质所具有的质量，即
密度的单位为kg/m3。
（3）温度 温度表示物体的冷热程度。法定计量单位中采用热力学温度，符号用T表示，单位为K（开）。摄氏温度用t表示，单位为℃（摄氏度）。它们之间的换算关系如下：
t=T-T0 （1-4）
式中，T0=273.15K。
（4）热力学能 热力学能是指热力系本身具有的能量（不包括热力系宏观运动的能量和外场作用的能量），包括分子的动能、分子力所形成的位能、构成分子的化学能和构成原子的原子能等。热力学能的单位为kJ。由于在热能和机械能的转换过程中，后两种能量不发生变化，故工程热力学能为
对于气体，分子动能包括分子的移动能、转动能和分子内部的振动能。
（5）焓和比焓 焓是一个组合的状态参数，其计算公式如下：
H=U+pV （1-5）
式中，H是焓（J）；U是热力学能（J）；p是压力（Pa）；V是体积（m3）。
比焓h是焓除以质量（H/m），单位为J/kg。
（6）熵和比熵 熵是一个导出的状态参数。对简单可压缩均匀系（即只有两个独立变量或自由度的均匀的热力系），它可以由其他状态参数按下列关系式导出：
式中，S为熵；S0为熵常数。
在法定单位制中，熵的单位为J/K，在工程单位制中，熵的单位为kcal/K。
比熵s是熵除以质量（S/m），单位为J/（kg·K）。(www.xing528.com)
7.平衡状态
平衡状态是指热力系在没有外界作用的情况下，宏观性质不随时间变化的状态。
处于平衡状态的单相流体（气体或液体），如果忽略重力的影响，又没有其他外场作用，它内部各处的各种性质都是均匀一致的。不仅流体内部的压力均匀一致（这是建立力平衡的必要条件）、温度均匀一致（这是建立热平衡的必要条件），而且所有其他宏观性质，例如：比体积、比热力学能、比焓、比熵等也都是均匀一致的。
处于气-液两相平衡的流体，流体内部的压力和温度均匀一致，但气相和液相的比体积（或密度）、比热力学能、比焓、比熵不同。
8.状态方程和状态参数坐标图
处于平衡（均匀）状态的热力系，两个相互独立的状态参数就可以规定它的平衡状态。在其他状态参数和这两个相互独立的状态参数之间，必定存在某种单值的函数关系。压力、温度、比体积这三个可以直接测量的基本状态参数之间存在v=f（p，T）的关系。这一函数关系称为状态方程。状态方程也可以写为如下隐函数的形式：
f（p，v，T）=0 （1-7）
9.热力过程和热力循环
热力过程是指热力系从一个状态向另一个状态变化时所经历的全部状态的总合。
热力循环就是封闭的热力过程，即热力系从某一状态开始，经过一系列中间状态后，又回复到原来状态。
10.功和热量
热力系通过界面和外界进行的机械能的交换量称为做功量，简称功（机械功）。它们之间的热能的交换量称为传热量，简称热量。功和热量是和热力系的状态变化（即过程）联系在一起的。它们不是状态量而是过程量。
功的符号是W，热量的符号是Q。对于单位质量的热力系，功用w表示，热量用q表示。热力学中通常规定：热力系对外界做功为正（W＞0），外界对热力系做功为负（W＜0）；热力系从外界吸热为正（Q＞0），热力系向外界放热为负（Q＜0）。
11.实际气体和理想气体
气体通常具有较大的比体积，气体分子之间的平均距离通常要比液体和固体的大得多。气体分子本身的体积通常比气体所占的体积小得多，气体分子之间的作用力（分子力）也较小，分子运动所受到的约束较弱，分子运动很自由。
在工程计算中，当气体的比体积不很大时，必须考虑气体分子本身体积和分子间作用力的影响时，把气体处理为实际气体。实际气体的性质比较复杂。
为使问题简化，热力学中提出理想气体的概念，即认为理想气体的分子本身不具有体积，分子之间也没有作用力，是由大量相互之间没有作用力的质点组成的可压缩流体。实际气体当比体积趋于无穷大时也就成了理想气体。这时分子间的作用力随着距离的无限增大而消失了，分子本身的体积比起气体的极大体积来也完全可以忽略了。
12.理想气体状态方程和摩尔气体常数
理想气体的状态方程为
或pv=RgT （1-8）
式中，Rg是气体常数。各种气体的气体常数不同，对于同一种气体，Rg是一个常数。气体常数的单位在我国法定计量单位中是J/（kg·K）。
如果对不同气体都取1mol，则式（1-8）变为
Mpv=MRgT或pVm=RmT （1-9）
式中，M是摩尔质量（kg/mol）；Vm是摩尔体积（m3/mol）；Rm是摩尔气体常数或通用气体常数，与气体种类无关。
13.理想混合气体
（1）混合气体的成分 工程上所遇到的气体有许多是若干种不同气体的混合物，例如天然气。如果将各组分的气体都按照理想气体计算，则称之为理想混合气体，简称混合气体。混合气体的成分可以用质量（m）、物质的量（n）、或体积（V）标出。通常都用标准状况下的体积标出。工程上常用相对成分表示（相对成分是各分量占气体总量的比值）。对理想混合气体来说，摩尔分数在数值上等于其体积分数。
（2）混合气体的平均摩尔质量和气体常数 混合气体的平均摩尔质量可以根据各组成气体的摩尔质量和各相对成分来计算。任何物质的摩尔质量都等于质量除以物质的量。混合气体的平均摩尔质量等于各组成气体的摩尔质量与摩尔分数乘积的总和。
知道了混合气体的平均摩尔质量后，就可以用摩尔气体常数除以平均摩尔质量而得到混合气体的气体常数：
（3）理想混合气体的压力与各组成气体的分压力 道尔顿定律指出，理想混合气体的压力（pmix）等于各组成气体的分压力（pi）的总和：
所谓分压力，就是假定混合气体中各组成气体单独存在，并具有与混合气体相同的温度和体积时给予容器壁的压力。
14.气体的热力性质
（1）气体的比热容 比热容定义为单位质量的物质发生单位温度变化时所吸收或放出的热量：
比热容的法定计量单位是J（kg·K），在工程单位制中是kcal/（kg·K）。1kcal/（kg·K）=4186.8J/（kg·K）
比热容不仅因物质和过程而异，而且还和压力和温度有关。对应于定容过程和定压过程，分别有比定容热容（cV）和比定压热容（cP）：
气体的比定容热容和比定压热容在计算热力学能、焓、熵及过程的热量等方面很有用。
（2）理想气体的比热容、热力学能和焓、迈耶公式 理想气体的热力学能仅是温度的函数，u=u（T）；理想气体的比焓也是温度的函数，h=u+pv=u（T）+RgT=h（T）。
根据理想气体的比定容热容和比定压热容，得
根据焓的定义式h=u+pv，微分后可得dh=du+d（pv）。对理想气体可写为
cp0=CV 0+Rg （1-17）
式（1-17）称为迈耶公式。它建立了理想气体比定容热容和比定压热容之间的关系。
因为理想气体的热力学能和焓都只是温度的函数，理想气体的比定压热容和比定容热容也都只是温度的函数。通常可以用三次多项式表示：
cp0=a0+a1T+a2T2+a3T3 （1-18）
cV0=（a0-Rg）+a1T+a2T2+a3T3 （1-19）
对不同气体，a0，a1，a2，a3各有不同的经验数值。
需要指出：单原子气体的比定容热容和比定压热容基本上是定值，可以认为与温度无关。对双原子气体和多原子气体，如果温度接近常温，为简化计算，也可将比热容看做定值。通常取298K（25℃）时气体比热容的值为比定压热容的值。
（3）理想气体的熵 根据熵的定义式
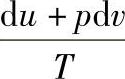，而对理想气体有du=cV0dT，
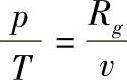，所以理想气体的熵为
v。理想气体的熵则不仅是温度的函数，它还和压力或体积有关。
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
