(1)Voronoi图
Voronoi图,又叫泰森多边形或Drichlet图,它是由一组由连接两邻点直线的垂直平分线组成的连续多边形组成。
①定义
假设V=v1,v2,v3,…,vn,n≥3是欧几里德平面上的一个点集,并且这些点不共线,四点不共圆。用d(vi,vj)表示vi,vj间的欧几里德距离。设x为平面上的点,则区域V(i)={x∈E2,d(x,vi)≤d(x,vj),j=1,2,3,…,n,j≠i}成 为Voronoi多边形。各点的Voronoi多边形构成Voronoi图。
②特点
a.Voronoi(S)把平面划分成n个多边形域,每个多边形域V(pi)包含且只包含S的一个点pi。
b.Voronoi(S)的边是S中某对点的中垂线的一个线段或者射线。
c.V(pi)是无界的,当且仅当pi属于凸包外界的点集。
d.Voronoi图至多有2×n-5个顶点和3×n-6条边。
e.每个Voronoi点恰好是三条Voronoi边的交点。即Voronoi点就是形成三边的三点的外接圆圆心,而且这些外接圆有个特点:各自内部不含任何S点集的点。
(2)Delaunay三角剖分
Delaunay三角剖分具有很好的理论基础和数学特性,一直占据网格剖分技术的主导地位。Delaunay三角网格是Voronoi图的几何对偶图,对它的研究是从对Voronoi图的研究开始的。
①定义
Delaunay边:假设E中的一条边e(两个端点为a、b),e若满足下列条件:存在一个圆经过a、b两点,圆内不含点集V中任何其他的点,则称为Delaunay边。
Delaunay三角剖分:如果点集V的一个三角剖分T只包含Delaunay边,则该三角剖分称为Delaunay三角剖分。
②Delaunay三角剖分的准则
要满足Delaunay三角剖分的定义,必须符合两个重要的准则:
a.空圆特性:Delaunay三角网是唯一的(任意四点不能共圆),在Delaunay三角形网中任一个三角形的外接圆范围内不会有其他点存在(图3-5①)。
b.最大化最小角特性:在散点集可能形成的三角剖分中,Delaunay三角剖分所形成的三角形的最小角最大。因此,Delaunay三角网是“最接近于规则化的”的三角网。即,在两个相邻的三角形构成凸四边形的对角线,在相互交换后,六个内角的最小角不再增大(图3-5②)。
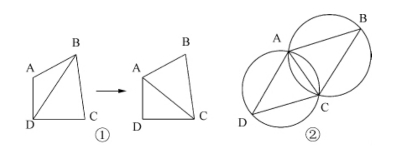
图3-5 Delaunay三角剖分的准则(https://www.xing528.com)
③Delaunay三角剖分的特性
a.最接近:以最近临的三点形成三角形,且各线段皆不相交。
b.唯一性:不论从区域何处开始构建,最终都将得到一致的结果。
c.最优性:任意两个相邻三角形形成的凸四边形的对角线如果可以互换的话,那么两个三角形六个内角中最小的角度不会变大。
d.最规则:如果将三角网中的每个三角形的最小角进行升序排列,则Delaunay三角网的排列得到的数值最大。
e.区域性:新增、删除、移动某一个顶点时只会影响临近的三角形。
f.具有凸多边形的外壳:三角网最外层的边界形成一个凸多边形的外壳。
④局部最优化处理
为了构造Delaunay三角网,Lawson提出了局部优化过程LOP(Local Optimization Procedure),一般三角网经过LOP处理,即可确保成为Delaunay三角网,其基本做法如下:
a.将两个具有共同边的三角形合成一个多边形。
b.以最大空圆准则作检查,看其第四个顶点是否在三角形的外接圆之内。
c.如果第四个顶点是在三角形的外接圆之内,修正对角线即将对角线对调,即完成局部优化过程的处理(图3-6)。
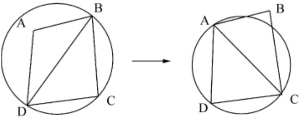
图3-6 LOP处理过程
⑤Delaunay三角网格的优势
a.Delaunay三角网格是一空间优化结构。在利用网格进行分析计算时,希望网格单元尽量饱满,这样可以使计算精度提高。而把点连成Delaunay三角形或四面体时,最能满足这个需求。
b.Delaunay三角网格的可操作性较好。Delaunay三角网格是Voronoi图的几何对偶图。它有严格的数学定义和完备的理论基础,一般情况下具有唯一性。在对已经生成的网格进行加点、减点操作时,有可靠的依据和简单的方法,可以确保得到的新网格仍然是Delaunay三角网格(图3-7)。
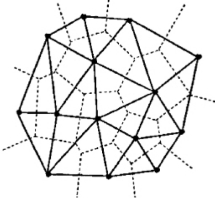
图3-7 Voronoi图与Delaunay三角剖分
注:实线表示Delaunay三角剖分,虚线表示Voronoi图
经典的Delaunay三角剖分技术已经比较成熟,近年来的研究重点是限定Delaunay三角剖分的边界恢复算法,以及如何克服薄元的问题。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




