基于空间灰色理论的人体扫描线点云孔洞修补技术

通过试验分析，上述方法不适合针对扫描线点云的孔洞修补。据前文所述，人体点云模型由若干条封闭的扫描线组成，同一条扫描线上的点位于同一扫描平面内，这些点存在必然的内在联系，同一扫描线上的点在一定程度处于一个空间灰色系统。因此，针对每条扫描线，建立空间灰色模型，利用原始点云数据预测新的点云数据，实现对扫描线的孔洞修补。

（1）空间灰色模型（SGM）的数学原理

灰色系统理论通过灰色生成来弱化数据序列的随机性并研究其内在的规律，通过建立灰色生成序列的微分方程，实现对无序数据序列的预测，从而为构造信息不完全的研究对象模型提供了一条可行的途径。

灰色系统理论主要通过灰色生成处理将原始无序数据序列变成有序数据序列，通过求解微分方程建立灰色动态模型。空间灰色模型解决的是空间点序列问题。

假设P是一组人体测量点序列：

P＝（p（t1），p（t2），…，p（tk），…p（tn）），k＝1，2，…，n

可以用以下数据序列表示原始数据序列：

P（0）＝（p（0）（1），p（0）（2），…，p（0）（k），…，p（0）（n）），k＝1，2，…，n

根据公式进行一阶累加生成，得到以下数据序列：

P（1）＝（p（1）（1），p（1）（2），…，p（1）（k），…，p（1）（n）），k＝1，2，…，n

一组新的数据序列可按公式2-2生成：

然后建立微分方程：

系数＝［a，b］T可通过最小二乘法（LSM）计算：

数据矩阵B和向量Y如下：

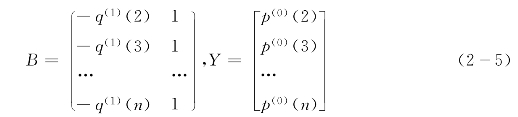
通过求解微分方程，得到p（1）（k）：

最后，通过累减生成计算预测值：

(www.xing528.com)

（2）扫描线点云空间灰色模型SGM（1，1）

每条扫描线上的点通过其空间坐标信息（x，y，z）共同决定该扫描线的运动趋势。上述测量点序列P可用下面的向量表示：

由于扫描操作特征，同一条扫描线上的点具有相同的y坐标，所以，此处只关注不同点间的x和z坐标值，建立扫描线点云空间灰色模型SGM（1，1）。

①坐标转换

根据灰色系统理论，数据序列为时间序列，要求数据序列不能为负值。因此，当测量点坐标值为负时，必须对其进行坐标转换。为便于处理，当数据序列p（tk）出现负值时，采用下面方法对其进行坐标转换。

这样，测量点数据序列可表示为：

②孔洞检测

在进行孔洞修补前，必须首先确定该条扫描线是否存在孔洞。根据扫描线特征，采用临近2点间弦长来进行孔洞检测。每条扫描线上临近2点弦长可构成下列数据序列：

｛d（1），d（2），…，d（k），…d（n）｝，

其中：

这里d（1）代表p（n）和p（1）间的弦长。通过分析整理弦长数据序列，去除异常数据，取其平均值¯d作为阈值来检测孔洞是否存在。若d（k）＞¯d，则孔洞存在。

③建立空间灰色模型SGM（1，1）

据上所述，通过孔洞检测，若存在孔洞，根据空间灰色模型基本原理，建立扫描线点云空间灰色模型：

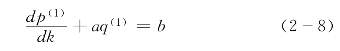
在本文的试验中，每条扫描线上的点按顺时针读取。如果只有1个孔洞，则扫描线上所有点用于建立模型；如果存在2个或2个以上的孔洞，则分段取点建立模型。每当一个新点生成时，则需按照孔洞检测方法重新检测孔洞是否存在，以决定是否需要生成新的点。

当处理完所有扫描线，就完成对点云模型的孔洞修补，结果如图2-9所示。

图2-9　孔洞修补后的人体点云模型