稳态行为下ASCS自身信息的故障检测和诊断方法研究

由9.2.1 小节中分析可知，ASCS 自身信息根据分布规律的特点可分为平稳信号和非平稳信号，其诊断先验知识见表9.1。本节分别针对平稳信号和非平稳信号提出相应的故障检测与诊断算法，并进行试验验证。

1.基于PCA 的ASCS 平稳随机信号的故障检测和诊断算法研究

稳态行为下ASCS 平稳随机信号的故障检测和诊断需充分利用信号服从一定分布规律的特点，因此对稳态行为下ASCS 平稳随机信号的历史数据进行挖掘，构建信号的分布规律，然后再将所构建的信号分布规律用于检测和诊断当前状态下系统信号，从而实现故障检测和诊断功能。

由于ASCS 平稳随机信号具有数据维数高、变量之间关系复杂等特点，采用单变量数据挖掘的方法只能检测过程变量的均值改变、阈值、方差，但却无法反映变量之间的相关关系，对于逻辑关系复杂的大型系统具有明显的不足。为了弥补此缺点，体现信号之间的相关关系，多变量统计（多元统计）被广泛地应用于工业过程监测，其典型理论有主元分析（principal component analysis，PCA）、因子分析、聚类分析等。本书选用多变量统计的主元分析方法来实现对ASCS 平稳随机信号的故障检测和诊断。

主元分析是一种降维的有效方法，它通过数据处理将高维数据以尽可能少的信息损失投影到低维空间，使数据降维，达到简化数据结构的目的。结合故障的定义，即系统至少一个特征属性或参数出现不可接受的偏差，PCA理论认为数据的变化是反映系统规律的指标，通过PCA 数据挖掘构建无故障的PCA 模型，之后运用PCA 模型计算当前系统状态变量的综合指标来反映系统状态变量的偏差，最终通过偏差的判断实现故障检测和诊断的功能。

传统PCA 算法在处理三维历史数据时，通常采用多向主元分析方法，但存在着主元模型存储空间需求大、模型之间冗余度高等问题，不利于实时故障检测算法的移植和实现。因此，在保证故障检测灵敏度的条件下，针对主元子空间数据矩阵结构进行研究以减小模型的冗余度和存储空间，同时提高主元模型对噪声的鲁棒性。

如图9.3所示，AMT 车辆从怠速状态起步，从2 挡升至5 挡。从系统轨迹中提取出系统稳态行为。选取稳态行为1 为研究对象（其余稳态行为方法类似），从历史数据中选择50 组无故障数据建立历史主元模型。其监控变量有挂挡行程位置TX （关闭电磁阀后标定参数值188）、选位行程位置TY （关闭电磁阀后标定参数值532）、离合器分离摆臂行程位置LC （离合器完全接合值144），采样时间为10 ms，取综合监控指标OIndex 控制限为11.345。

相对于传统PCA 模型，由于对子空间数据结构的优化，改进的PCA 模型具有运算量小、存储量少、对噪声鲁棒性好的优点。图9.4 （a）是将实车稳态行为1 中变量输入传统PCA 模型中的故障检测结果，图9.4 （b）是将实车稳态行为1 中变量输入改进PCA 模型中的故障检测结果。从检测结果中可知，在无故障时OIndex 指标远远小于控制限阈值11.345，此时诊断结果与实际吻合，ASCS 系统平稳变量正常。

在实际工程应用中，测量噪声是无法避免的，为了验证故障检测算法对噪声的判断，向稳态行为1 中的平稳变量分别加入高斯噪声，同时运用不同主元分析模型去检测，其故障检测结果如图9.5所示。

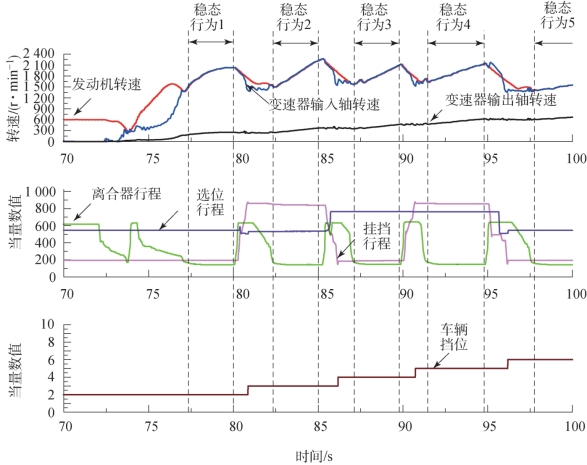
图9.3　实车ASCS 采集数据

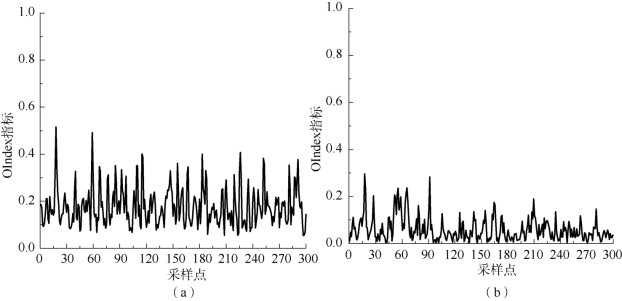
图9.4　实车稳态行为故障检测结果

（a）基于传统PCA 故障检测OIndex 指标；（b）基于改进PCA 故障检测OIndex 指标

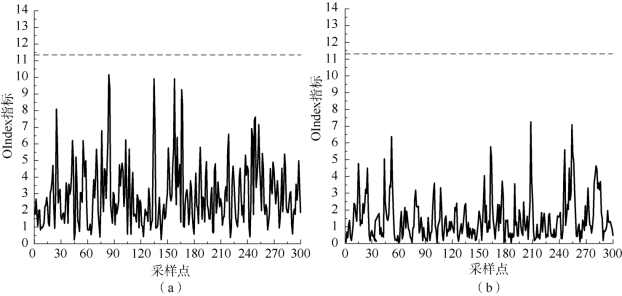
图9.5　噪声干扰下稳态行为故障检测结果

（a）基于传统PCA 故障检测OIndex 指标；（b）基于改进PCA 故障检测OIndex 指标

在图9.5 （a）中采用传统PCA 模型进行故障检测，在采样点87 和采样点135 的时候综合统计指标OIndex 接近设定阈值，若超出虚线（11.345）则认为ASCS 系统在该时刻的平稳变量之间的马氏距离不符合历史模型，若噪声加大则可能会引起故障误报。与之相比较在图9.5 （b）中，检测结果与设定阈值有一定余量，可见改进的PCA 模型对系统噪声具有更好的鲁棒性。

为了验证故障检测算法对噪声与故障的区分能力和灵敏性，向稳态行为1平稳变量中同时加入噪声和单一故障，如图9.6所示。在采样点100 时向选位行程TY 注入故障，故障类型为传感器均值异常，同时运用不同主元分析模型进行故障检测。检测结果如图9.7所示，通过检测结果图（a）、（b）对比可以发现，在故障发生之前均未发生故障误报，在采样点100 处监控指标OIndex 数值迅速上升，超出故障检测阈值，同时通过对比综合统计指标数值可以发现，基于改进PCA 的主元分析模型对故障更加灵敏。

为了体现故障检测算法对故障的跟踪能力，向稳态行为1 平稳变量TX 同时加入噪声和间隙性故障（正弦信号），故障注入如图9.8所示。

运用改进的PCA 模型进行故障检测，检测结果如图9.9所示。

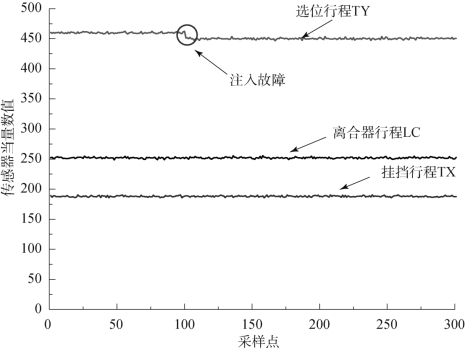
图9.6　稳态行为TY 故障注入(www.xing528.com)

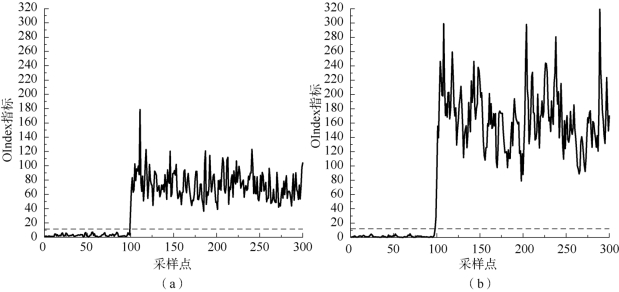
图9.7　实车稳态行为TY 故障注入的检测结果

（a）基于传统PCA 故障检测OIndex 指标；（b）基于改进PCA 故障检测OIndex 指标

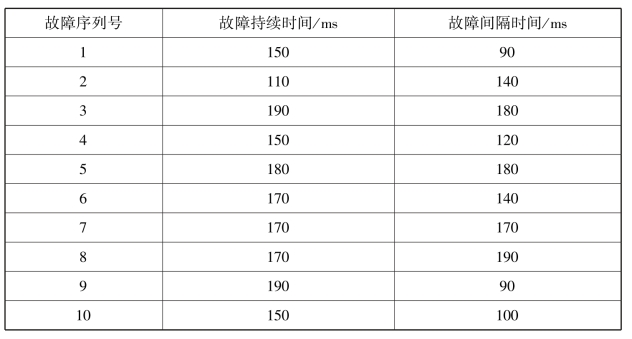
故障检测指标OIndex 超过阈值则认为系统稳态行为出现异常，图9.9 中用柱框标明，总共出现完整的9 次柱框（第10 次不完整），即认为出现了9次持续性故障，故障区间分别与波峰和波谷一一对应，故障诊断结果与注入故障（正弦故障）的特性吻合。统计超出故障检测阈值的故障持续时间和间隔时间，如表9.3所示，柱框的持续时间以及间隔时间基本一致，但是细节上均呈现出正态分布趋势，这是由测量噪声的正态分布特点所引起的。

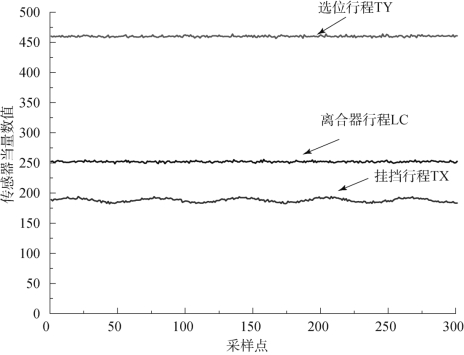
图9.8　稳态行为TX 故障注入

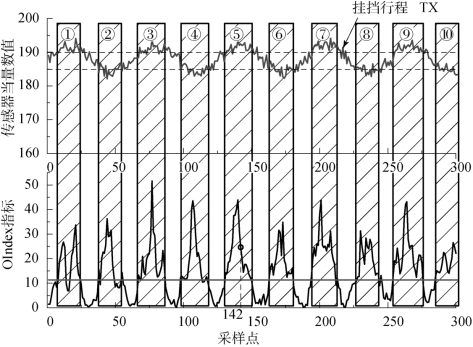
图9.9　稳态行为TX 故障检测图

将柱框投影到挂挡行程TX 数据曲线中，柱框所包含的挂挡行程数据用虚线标注。从整体的角度观察，可明显发现柱框所对应的挂挡行程数据，几乎全部集中在TX 曲线的波峰和波谷部分，也就是说当TX 数值与中心绝对误差过大时，监控指标超出设定阈值，认为故障发生。监控指标OIndex 数值与TX数值的趋势一致性说明故障检测算法对故障具有良好的跟踪性。同时在虚线部分之内则认为系统稳态行为正常，说明故障检测算法对数据自身波动有一定的冗余性。

表9.3　故障持续时间以及间隔时间统计

当故障检测算法发现ASCS 系统异常稳态行为后，将故障检测结果和三个ASCS 系统平稳变量输入故障诊断算法模块中，搜索导致监控指标OIndex 超过阈值的原因，即寻找对系统偏差贡献最大的平稳变量。

当ASCS 系统监控指标超出设定阈值时，各个采样点对应着不同的主元子空间模型，由于篇幅限制，这里省略。

2.ASCS 非平稳随机信号的故障检测和诊断方法研究

在ASCS 稳态工况过程中存在一类信号，它是驾驶员意图的衍生物，即动力系统的转速信号。驾驶员通过油门脚踏板和制动脚踏板来调整车辆速度，从而满足车辆行驶的速度需求。不同路况、不同时间、不同驾驶员产生不同车辆行驶速度的要求，即车辆速度信号在时间轴上的分布没有固定的规律，或分布参数随时间发生变化（非平稳性），因此很难用历史数据来分析或估计当前信号的参数。

虽然无法用历史数据来诊断当前ASCS 非平稳信号，但可利用系统硬件平台的自身结构来获得故障检测和诊断的先验知识，主要有以下两种诊断方法。

1）单信号诊断

单信号诊断仅针对信号自身，利用频谱分析、时域极值分析等手段，实现信号自身的故障诊断功能。单信号诊断的先验知识和故障阈值需要根据具体硬件平台信息而确定。

2）基于数学解析模型的故障诊断方法

当离合器处于接合状态时，转速之间存在一定的冗余关系：

式中，ig 为当前挡传动比；其余参数同前。

通过信号之间的数学关系来分析当前ASCS 系统转速信号的状态，从而实现故障诊断的功能。