基于DP的换挡序列优化策略

1.优化问题的确定

本节针对已知坡度的道路，利用DP 求解出AMT 重型越野车辆在一定路程内行驶时平均运行速度和燃油消耗量加权最优的换挡序列。

动态规划是解决多阶段决策问题的一种方法，重型车辆在一定路程L 内的综合性能最优换挡序列的求解，则可以看作求解一系列车速和挡位下，随着时间变化，换挡指令和节气门开度变化的一系列阶段性决策。

针对该优化问题，首先需要确定出模型的阶段、状态变量、决策和策略、状态转移、指标函数等。按照空间特征将总路程等分为N 个相互离散的阶段，每个阶段的步长（距离）为h，单位m，那么有L ＝N×h。另外，以k 作为不同阶段的阶段变量。选择阶段k 内的运行速度ve、挡位ge 和广义道路阻力系数β 作为相应阶段的状态变量，记作

根据重型车辆的特点，考虑无制动的纵向控制，选取的决策变量为换挡指令ug 和节气门开度ut。第k 阶段决策变量如式（4.69）所示。

关于状态转移关系，运行速度ve 和挡位ge，其状态转移方程参照式（4.70）和式（4.71），其中加速度ak 由车辆行驶方程计算获得。根据广义道路阻力系数β 的计算式可确定其状态转移关系，如式（4.72）所示，其中f为滚动阻力系数，α 为道路坡度。

优化的目的在于在保证重型车辆动力性能的前提下尽可能降低燃油消耗，因此选用每个阶段的运行耗时tk（s）和阶段油耗量ms，k（g）的加权和作为阶段指标函数。由于运行耗时和阶段油耗的数量级水平相同，故选用归一化加权因子，运行耗时的加权因子选为fβ∈（0，1），则阶段油耗量的加权因子为1－fβ，式（4.73）所示为本优化问题的阶段指标函数。

其中，

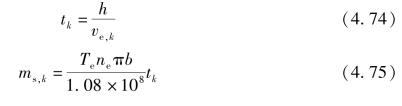
2.DP 的变量约束

考虑到该重型越野车辆的运行环境较为复杂，除了常规的铺装道路上运行速度较高外，陡坡爬行等工况下运行速度很缓慢，因此其运行速度ve 范围较广，其取值范围可以简化如下：

式中，vmin和vmax分别表示允许的最小运行速度和最大运行速度。相应地，不同速度对应于不同的挡位和发动机转速。本重型越野车辆配备的发动机怠速为600 r／min，最高空载转速为2 300 r／min，其理想工作转速在2 100 r／min 以下，考虑到DP 计算的可行性，设定发动机转速软约束如下：

该AMT 为9 挡有级式变速器，在DP 计算中将爬挡设为ge ＝1，1 挡至8挡设为ge ＝2 ～9。AMT 换挡序列所允许的挡位变化除了顺序升降挡外，还需要考虑极端道路条件下的跳降挡和跳升挡，本优化问题不考虑制动过程的影响，并尝试设定最多允许跳降3 挡，跳升2 挡，故挡位ge 和换挡指令ug 的约束如式（4.78）和式（4.79）所示。

为了限制AMT 的换挡频率，保证动力中断之后速度损失有足够时间恢复，规定相邻两次换挡过程之间时间间隔约为3 s。如果上一个阶段换挡指令ug，k－1不为零，且当前阶段耗时满足1.5 ＜tk ＜3，那么当前阶段的换挡指令赋值为ug，k ＝0。如式（4.80）所示，利用阶段耗时tk 对换挡指令ug，k进行约束。

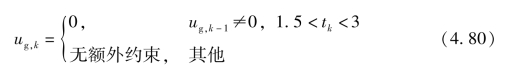(www.xing528.com)

决策变量中的节气门开度ut 也有一定限制，即0 ～100%，为了便于建立动态规划的变量网格，规定每5%为一个间隔，故节气门开度ut 的约束表示如下：

3.优化模型建立及DP 的实现

1）优化模型建立

根据主要参数的定义和变量约束，可以确定该优化问题的数学模型，表示优化目标在于获取最优的换挡指令和节气门开度变化序列，即最优策略，使得系统全局的目标函数值J 取得最小值。

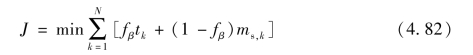
约束如下：

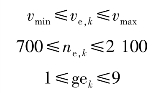
2）变量网格简化

按照4.6.1 小节介绍，进行一次全局优化的计算量至少为N ×m ×n 次，该数值可能相当巨大，为了提高计算效率，对状态变量进行适当的简化是十分必要的。下面分别针对状态变量和决策变量简化变量网格。

划分好阶段个数N 后，各个阶段的速度ve 和挡位ge 是不确定的，广义道路阻力系数也有所差别。根据发动机转速范围和不同挡位的总传动比可以确定出每个挡位下的运行速度范围，根据挡位与运行速度的对应关系可以对状态变量的组合进行预处理。图4.37所示为状态变量示意图，横坐标分别为阶段和挡位，纵坐标为速度（m／s），假设广义道路阻力系数和阶段一一对应，故在该示意图中没有绘出。

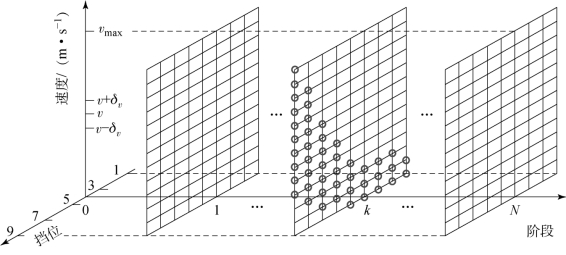
图4.37　状态变量示意图

在每个阶段中都包含挡位和运行速度的二维组合，即图中的网格交点。令速度的离散步长为Δv m／s，由于AMT 共9 个前进挡，可得该组合共m ＝9［（vmax－vmin）／Δv +1］个元素。例如，ge ＝1 时运行速度在0.609 ～2.539 m／s，删除运行速度在该范围之外的所有取值，可以减少ve 可能的取值个数，进而大幅减小m 的值。在图4.37 的网格交点中，阶段k 里圆圈表示简化后的状态变量网格。

3）考虑AMT 换挡特性的DP 改进

本优化问题重点考虑了AMT 的换挡特性，即换挡过程中离合器分离与再次接合之间存在动力中断，在此期间发动机与传动系统完全分离，重型车辆依靠惯性继续运行。当车辆在上坡行驶时，换挡必然面临着运行速度的损失。在DP 算法中相邻两个阶段如果发生换挡，即使换挡完成后车辆能提供更大的驱动力，运行速度仍会出现先下降再上升的情况。此时ve 的状态转移方程不再参照式（4.70），而是将该状态转移分为两个部分：动力中断部分和动力恢复部分。可以简单地认为动力中断部分的驱动力完全为零，则在动力中断时间内车辆仅受到相应阻力的作用。

为了便于计算，同时避免DP 无法获得可行解，此处设定动力中断时间toff ＝1.0 s，而没有按照二次挡位决策选用1.6 s。动力恢复部分是利用剩余的阶段耗时进行速度恢复，与在挡运行时状态转移方程类似。

综上，该优化问题中运行速度ve 的状态转移方程需要根据当前阶段的决策换挡指令ug 来确定，如式（4.83）～式（4.85）所示，ug，k ＝0 时状态转移方程与式（4.70）原理相同；否则分别根据动力中断期间的加速度aoff和动力恢复期间的加速度aon与时间tk－toff进行计算。需要注意的是，如果tk－toff小于零，说明运行速度较快，此时令toff ＝tk 即可。

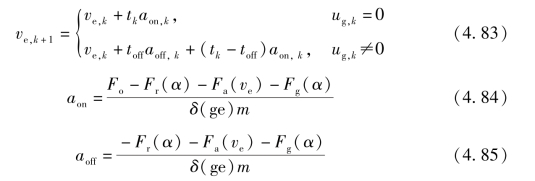
另外，除了换挡过程中动力性能的差异，也考虑了换挡过程中的燃油效率。通常的做法是用怠速过程的燃油消耗率代替换挡过程中的燃油消耗率，但结合本平台自身的特性，换挡过程中发动机转速并未下降至怠速，故动力中断过程与在挡过程的燃油消耗量差异忽略不计，均使用在挡时的油耗计算方法。