动态规划及其应用

1.动态规划

动态规划是应用数学的一个实用分支，它是解决优化问题的一种特殊途径。20 世纪50年代初Bellman 等人在研究多阶段决策过程的优化问题时，提出了最优化原理，即“每个最优策略只能由最优子策略组成”，通过把多阶段问题的优化转化为一系列单阶段问题的优化，并逐个求解单阶段的最优解，建立解决这类决策过程优化问题的新方法——动态规划。

严格来说，动态规划不算是一种算法，只是求解多阶段优化的方法。因而，它没有固定的数学表达式和明确定义的规则，而必须针对优化问题进行具体分析，所以动态规划的特点和主要问题在于优化模型的建立。动态规划主要用于求解以时间划分阶段的优化问题，对于其他静态规划可人为地引入时间因素，将其转化为多阶段决策过程，即可使用动态规划方法进行优化求解。

2.DP 方法的关键要素

DP 针对不同的问题具有不同的优化模型，因而构造DP 的优化模型对于优化问题的求解至关重要。一个多阶段决策过程最优化问题的动态规划模型通常包含以下几个要素。

（1）阶段。阶段是整个决策问题的自然划分。通常，DP 根据时间或者空间顺序的特征分解为若干相互联系的阶段，便于按照阶段号依次对优化问题求解。阶段变量一般用k ＝1，2，…，N 表示，N 为划分出的阶段总数。

（2）状态变量。状态变量表示每个阶段开始时的客观条件，或说每个阶段开始时与优化过程相关的特征。状态应该具有无后效性，简单来说就是下一个阶段的状态只和当前阶段有关，而与该阶段以前的各个阶段状态无关，这是动态规划问题可解的标志之一。通常要求状态是直接或间接可观的。

描述状态的变量称为状态变量，阶段k 的状态变量可以用sk 表示，状态变量可以是一个数或者一个向量。如果状态变量是连续变量，在数值计算中需要按照精度要求进行离散化。阶段k 内所有状态变量允许的取值范围称为状态集合，用Sk 表示，其中i 代表可能的状态变量个数，下文中含义相同，i ＝1，2，…，m。

（3）决策与策略。选定各个阶段的状态后，根据其状态可以做出不同的选择或决定，从而确定下一阶段的状态，称为决策。描述决策的变量称决策变量，用uk 表示，则uk（sk）表示针对第k 阶段的状态变量而选择的决策。如果uk 是连续的，在数值计算中需要进行离散处理。同样，决策变量uk 的取值也限制在一定范围内，该范围称为允许决策集合Dk，其中j 为决策变量可能的取值个数，下文亦同，j ＝1，2，…，n。

各个阶段的决策确定后，各阶段的决策序列构成一个策略，由第k 阶段到第j 阶段的子过程策略记作pk， j ＝｛uk（sk），…，uj（sj）｝。针对每个实际的问题，可供选择的策略也存在一定范围，称为允许策略集合，相应地，用Pk，j表示。其中使整个优化问题达到最优效果的策略叫作最优策略，记作

（4）状态转移方程。通常动态规划中下一个阶段k +1 的状态变量sk+1是当前阶段状态变量sk 和当前阶段决策uk（sk）共同作用的结果，它们之间的关系称为状态转移方程，表示为

（5）指标函数。指标函数用于衡量所选定策略优劣的数量指标，分为阶段指标函数和过程指标函数。阶段指标函数是指第k 阶段从状态sk 出发，采取决策uk 时产生的效果，记作ck（sk，uk）。

(www.xing528.com)

从第k 阶段开始，状态变量sk 采用策略pk，N后所产生的效果称为过程指标函数，记作Vk，N（sk，pk，N）。指标函数应该具有可分离性，即某一个阶段的指标函数可以表示为当前阶段状态变量、决策变量和相邻阶段指标函数的函数。常见的指标函数形式有阶段指标之和 （将所有阶段的指标函数相加）、阶段指标之积（所有阶段指标函数相乘）。最优指标函数表示从第k 阶段状态sk 采用最优策略到过程终止时的最佳效益值，记作fk（sk），即

3.DP 的逆序数值解法

以固定始端、自由终端、指标函数取和的形式进行DP 逆序数值解法说明。一般自由终端条件为

固定始端的条件可表示为S1 ＝｛s1｝。其中φ 为已知量，表示终端阶段的指标函数，取值为0 即可。根据式（4.59）和式（4.60）可知，状态转移方程和阶段指标需要针对阶段k 内状态集合Sk 的每一个取值sk，i和允许决策集合Dk（sk，i）的每一个取值u（j）k，i 进行计算，故可以将动态规划数值计算的基本方程表示如下：

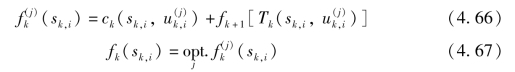
按照式（4.65）～式（4.67）逆序计算出f1（s1）即为全过程最优值。逆序计算的方法可以简述为：从第N 阶段开始进行计算，即根据该阶段所有可能的状态和相应的决策计算所有可能的指标函数值，通过比较确定出最优的阶段指标函数值及其对应的状态变量和决策。随后，阶段号k 逐次递减并搜索当前阶段所有状态变量中满足状态转移关系的特定状态变量，基于此状态变量和相应的决策再次计算该阶段的最优指标函数，根据状态转移关系累加该阶段及之后所有阶段的最优指标函数值，并确定最优的过程指标函数值和状态轨迹与策略，依此类推直到k ＝1，从而确定出最优状态轨迹和最优策略。DP 逆序数值计算流程如图4.36所示。

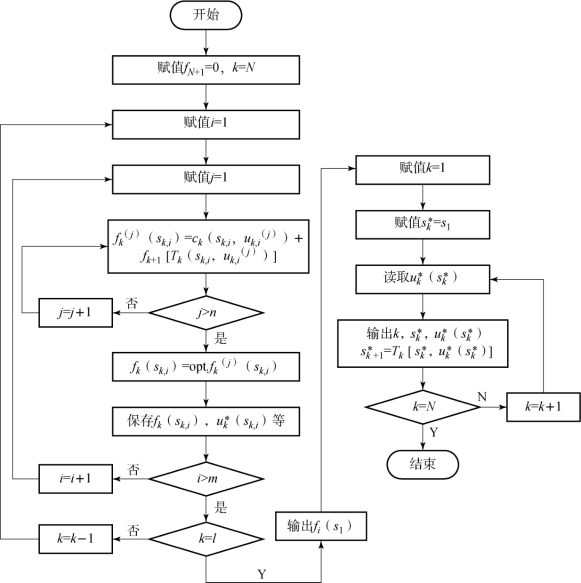
图4.36　DP 逆序数值计算流程

其具体过程可以表示为以下步骤。

第一步，令阶段N+1 的指标函数值为零，即fN+1 ＝0。

第二步，令k ＝N，计算阶段k 的最优阶段指标fk ＝ck（sk，uk）+fk+1和最优决策

第三步，取k ＝N－1 阶段的所有状态和决策进行计算，根据状态转移关系搜索出k 阶段中能够转移到k +1 阶段sk+1 的状态变量sk 及其最优决策进而累加k 阶段到N 阶段的最优指标函数值fk。

第四步，依次取k ＝N－2，N－3，…，1，并重复第三步。

第五步，最终求出全局最优指标函数值f1，并确定出最优状态轨迹和最优策略。

第六步，为了保证计算的准确性，在逆序确定出全局最优指标函数和相应的状态轨迹与策略后，利用顺序递推对上述计算结果进行验算，并输出全局最优指标函数值、最优状态轨迹和最优策略等。