二次挡位的选择策略

1.二次挡位决策概述

现有的自动变速操纵系统主要采用两参数换挡规律，即以车速和油门开度为选择不同挡位的依据。但是，目前两参数换挡规律换挡点的确定都是假设车辆换挡过程耗时很短，且忽略换挡时行驶阻力对车辆的影响，因此认为换挡过程中没有车速变化。即使是三参数换挡规律，其制定和计算也是基于一定假设的。然而，实际车辆在换挡过程中需要考虑的因素包含以下两点。

（1）换挡耗时的影响。AMT 是在手动变速器的基础上加装自动变速操纵系统组成的自动机械变速器，其收到换挡控制指令后，逐步完成相应的换挡操纵。换挡过程包含了离合器分离、摘空挡、变速器选挡（含变速器主箱选位、副箱换挡）、变速器主箱挂挡、离合器接合等一系列动作，且各个操作之间仅部分时间是重叠的。因此，AMT 重型越野车辆的整个换挡过程耗时相对一般的轿车是比较长的，根据目前的试验数据粗略统计，除起步外正常行驶时，试验车辆的换挡过程耗时在0.5 ～1.6 s，而在降挡过程换挡耗时将稍大于升挡，在复杂路况下换挡耗时又可能更大。几乎在整个换挡过程中，发动机与变速器输入轴是分离的，车辆动力传递发生中断。显然，换挡过程耗时是不能简单忽略的。

（2）外部行驶阻力的影响。AMT 在换挡过程中有动力中断，车辆除了下坡外，外部阻力之和一般不会为零，因而车速在换挡前后不可能保持不变。特别地，AMT 重型越野车辆在上坡换挡过程中，动力中断时间较长，在坡道阻力的影响下导致车速显著下降，进而使得换挡完成后，初始目标挡位无法与换挡后的车速获得良好的匹配，降低车辆的动力性能。在复杂路况下，即使不考虑换挡过程耗时的影响，由于车辆外部阻力的变化也会导致挡位与车速匹配不合理现象。

因此，在复杂工况下分析车辆行驶环境因素，尤其是估计车辆道路负载对车辆运行状态的影响十分必要，通过估计道路负载进行合理的挡位决策以提升重型AMT 车辆的动力性能具有重要意义。本节利用上文识别出的广义道路阻力系数β 作为车辆换挡控制的一个输入，进行上坡行驶的挡位决策。

2.二次挡位决策的制定

基于广义道路阻力系数β 进行二次挡位决策是对现有车辆自动换挡控制的一种补充，即在复杂路况下对多维参数换挡规律的扩充。在较小的道路负载下，认为无须采用二次挡位决策，直接按照多维参数换挡规律确定的换挡时刻和初始目标挡位进行换挡即可；在较大道路负载下，AMT 重型越野车辆换挡过程动力中断可能导致车辆连续换挡反而使得车速不断下降，为了避免出现这种极端的情况，采用二次挡位决策方法，利用车辆行驶过程中的广义道路阻力系数识别，或在换挡过程中利用动力中断判断道路负载大小，进而重新进行挡位决策，确定出新的目标挡位，而换挡时刻仍旧根据多维参数换挡规律确定。

1）广义道路阻力系数阈值的确定原则

本书中广义道路阻力系数阈值的值对于改进换挡策略具有决定性作用。无论初始目的挡位是几挡，在计算广义道路阻力系数阈值时都需要遵循以下几个原则。

第一，防止换挡后驱动力小于道路阻力。为了确保发动机提供足够的力量使车辆稳定行驶，需要计算出一个允许的广义道路阻力系数，使得驱动力能够克服道路阻力或者至少等于道路阻力。

第二，防止离合器转速过低或过高。由于换挡过程存在动力中断，在离合器接合后发动机转速被拖低。如果发动机转速低于怠速或者高于最高稳定转速，则计算出的广义道路阻力系数阈值不能作为挡位决策的辅助控制参数。

第三，需要满足与试验车辆相关的其他原则。例如，试验车辆原有的换挡控制策略在升挡时仅能顺序升至当前挡位相邻的高挡位，但是能降挡至相邻低挡位，或者跳降两个挡，甚至三个挡。

2）升挡广义道路阻力系数阈值的计算

如果通过原有两参数换挡规律或多维参数换挡规律确定的初始目标挡位比当前挡位高，则挡位决策转化至升挡模式。在计算顺序升挡广义道路阻力系数阈值βup时，由于换挡过程的动力中断，上坡时车速和离合器转速均会下降，在换挡后发动机转速最终被离合器拖低，导致发动机实际转速与发动机调速控制的目标转速不相等。顺序升挡的极端情况是换挡后发动机输出扭矩刚好等于当前的道路阻力。基于此极端情况可以求出顺序升挡时的广义道路阻力系数阈值βup，按照简化的车辆动力学模型，对应的换挡后车辆行驶方程可以近似地表示为如下公式：

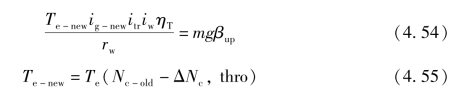
式中，Te－new为换挡后发动机输出扭矩；ig－new为变速器目标挡位的传动比；βup为顺序升挡广义道路阻力系数阈值，即在顺序升挡时所允许的最大广义道路阻力系数值；Nc－old为当前换挡规律中升挡点对应的离合器转速；ΔNc 为动力中断导致的发动机转速变化值，此时其中的β ＝βup；Δt 同上文定义一致，为动力中断时间，在此我们选取Δt 为1.6 s。另外，为了便于计算广义道路阻力系数阈值，可以将式（4.55）对应的发动机扭矩特性图转化为不同油门开度下的分段线性函数。例如，图4.27所示为试验车辆发动机外特性曲线，其中实线为试验测得的外特性曲线，人为将该曲线划分为①～④四个转速范围，并用一次函数拟合出各个转速范围内发动机扭矩随转速变化的关系，如图中的虚线所示。

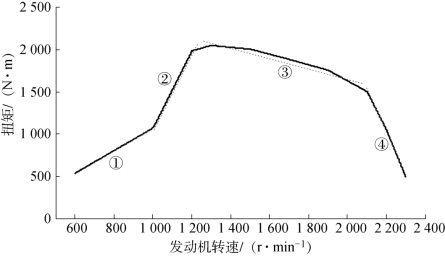
图4.27　试验车辆发动机外特性曲线

如式（4.57）所示，为拟合得到的100%油门开度下近似发动机扭矩特性表达式。

按照广义道路阻力系数计算公式，可以求出初始挡位为C 挡以外，各个油门开度下的顺序升挡广义道路阻力系数阈值，图4.28所示为试验车辆顺序升挡广义道路阻力系数阈值变化曲线。

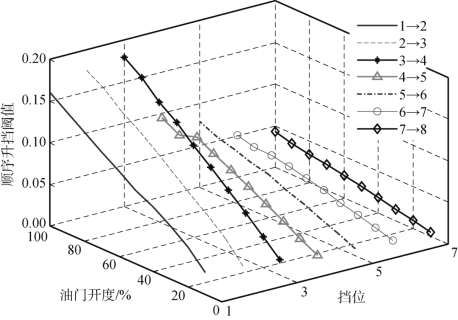
图4.28　试验车辆顺序升挡广义道路阻力系数阈值变化曲线

3）降挡广义道路阻力系数阈值的计算

如果通过原有两参数换挡规律或多维参数换挡规律确定的初始目标挡位低于当前挡位，则激活降挡挡位决策模式。由于降挡模式包含顺序降挡和非顺序降挡，因此广义道路阻力系数阈值需要根据实际降挡情况进行计算。类似于顺次升挡的阈值计算，降挡情况下广义道路阻力系数阈值也可以根据降挡后发动机扭矩刚好克服当前道路阻力的等量关系计算，车辆降挡后的运动方程和式（4.54）～式（4.56）相似。图4.29所示为试验车辆在不同油门开度下降挡时广义道路阻力系数阈值变化曲线，其中βd1，βd2分别表示顺序降挡至相邻较低挡位，跳降两挡的广义道路阻力系数阈值。

4）基于阈值计算的上坡挡位决策

根据上文介绍，改进的上坡挡位决策框图如图4.30所示，其中虚线框内为本章的主要研究内容。4.5.2 小节对RLS 识别方式进行介绍，上文说明了广义道路阻力系数阈值的计算方法，并求出针对该试验车辆的相应升挡和降挡广义道路阻力系数阈值。图4.30 中采用的是带多遗忘因子的RLS 算法，运用AMT 重型越野车辆动力学模型对整车质量m 和广义道路阻力系数β 进行识别。

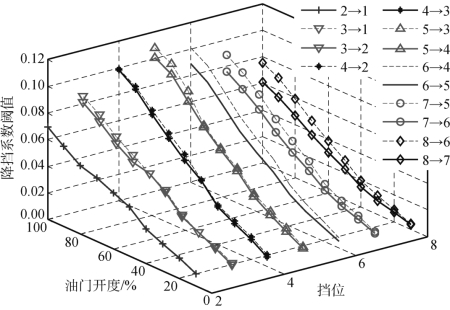
图4.29　试验车辆在不同油门开度下降挡时广义道路阻力系统阈值变化曲线(www.xing528.com)

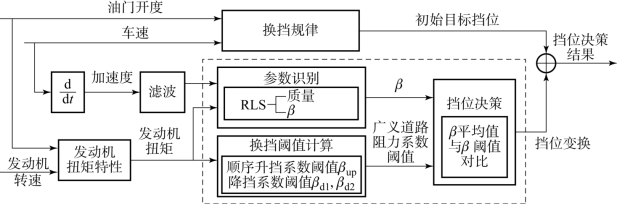
图4.30　改进的上坡挡位决策框图

改进的上坡挡位决策方法是在多维参数换挡规律基础上，增加挡位决策模块。参数估计模块的结果和预先计算获得的广义道路阻力系数阈值则作为挡位决策的输入。一定条件下，多维参数换挡规律确定了换挡时刻和初始目标挡位。随后，挡位决策模块通过对比估计出的广义道路阻力系数与对应油门开度和挡位下的阈值，来确定最终是升挡、降挡还是保持当前挡位。

TCU 计算好当前时刻前3 s内的广义道路阻力系数估计值的平均值avg.（β），在进入升挡模式时，TCU 对比avg.（β）与对应顺序升挡广义道路阻力系数阈值βup，如果该平均值小于对应βup，则经过修正的目标挡位为升挡至相邻较高挡位，否则保持当前挡位行驶。进入降挡模式时，如果avg.（β）小于βd1，则TCU 操控执行机构换至相邻较低挡位，如果avg.（β）大于βd1且小于βd2，则跳降两个挡位；如果avg.（β）大于βd2，则跳降三个挡位。为了避免跳降太多挡位导致发动机调速过程转速过高，限制降挡的最大数目为三个挡位。上坡挡位决策流程简图如图4.31所示。

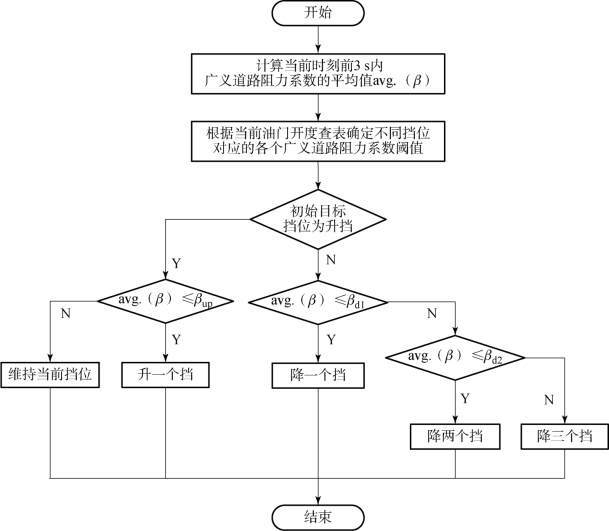
图4.31　上坡挡位决策流程简图

5）动力中断期间的挡位决策

考虑到换挡过程中外界阻力发生变化的特殊情况，在AMT 重型越野车辆换挡的动力中断期间也可能需要进行相应的挡位决策。由于动力中断期间发动机提供给车辆的动力视为零，故车辆只受到外界阻力的影响，凭借车速的变化即可确定出动力中断期间的加速度a，进而求出近似的广义道路阻力系数β，即

然而，考虑到动力中断过程本来是用来执行换挡操纵的，如果用于计算近似广义道路阻力的时间太长，则TCU 不能够及时做出判断，无法在变速器选挡前完成二次挡位决策。因此人为设定用于估算加速度的时间从离合器开始分离后约100 ms 开始，至摘空挡开始后一段时间（需要根据实际情况进行标定）为止，但是需要保证在完成摘空挡时已经确定最终目标挡位。

确定了近似的广义道路阻力后，采用条件判断的方式实现动力中断期间的二次挡位决策。首先，判断β 是否大于零，一般情况下仅在下坡时会出现广义道路阻力（系数）为非正数。如果β 非正数，则应考虑下坡行驶的挡位决策方法；否则依照4.5.3 小节中2.4 中的方法进行上坡行驶的挡位决策。

在动力中断期间进行广义道路阻力系数的估计，不需要发动机的扭矩特性，也无须加装加速度传感器，但是由于可供数据采集和计算的时间太短，往往估计结果不够准确，所以仅考虑动力中断期间的识别结果用于定性识别，辅助二次挡位的决策工作。

3.二次挡位决策的仿真

不局限于使用该二次挡位决策方法对多维参数换挡规律的扩充，在目前的AMT 重型越野车辆中，在原有的两参数换挡规律基础上也可以使用该方法来改善车辆的动力性能。另外，下坡行驶时，为了有效利用发动机制动的效能，同时兼顾驾驶员的控制意图，除了广义道路阻力系数β 外，需要配合油门开度、制动等信号，来对下坡过程的挡位控制进行相应的挡位决策。

图4.32 对比了使用原有的换挡策略和改进后的挡位决策时升挡模式下的仿真结果。图4.32 （a）给出了预设的广义道路阻力系数β，β 从初始的0.02升至0.19 （约第15 s），最终降至0.17。原有的换挡策略和改进后的挡位决策均是基于此预设的广义道路阻力系数，并保持油门开度100%。

根据图4.32 （b）和（c），随着广义道路阻力系数的增加，车辆从4 挡依次降至3 挡，随后降至2 挡，同时车速也逐渐下降。然而，图4.32 （b）显示使用原有换挡策略时，22 s后出现了2 挡与3 挡间的循环换挡，最低车速降至约3.3 m／s，而最高车速为4.4 m／s。作为对比，图4.32 （c）使用了改进的挡位决策，由于广义道路阻力系数大于0.18 并始终大于对应的广义道路阻力系数阈值，因此在22 s后经修正的目标挡位保持在2 挡，同时车速逐步提升至4.7 m／s。

图4.32　升挡模式挡位决策仿真对比

（a）预设广义道路阻力系数β；（b）原有换挡规律；（c）改进的挡位决策

降挡模式挡位决策仿真对比如图4.33所示。从曲线的对比可知，在广义道路阻力系数较小时，改进的挡位决策并未改变原有换挡规律确定的目标挡位；广义道路阻力系数增大并超过βd2后，原换挡规律下车辆逐渐从5 挡依次降至3 挡，35 s时车速为4.4 m／s；采用二次挡位决策并考虑跳降挡个数限制，20 s后车辆从5 挡直接降至3 挡，最终车速保持在4.8 m／s。类似于升挡模式的控制，改进后的挡位决策方法同样减少了换挡次数，并提升了整体车速。

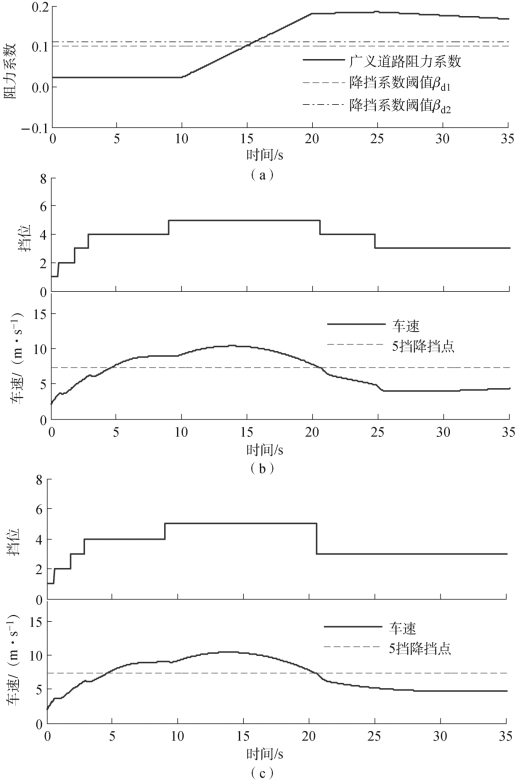
图4.33　降挡模式挡位决策仿真对比

（a）预设广义道路阻力系数β；（b）原有换挡规律；（c）改进的挡位决策

4.二次挡位决策的实车数据分析

图4.34 和图4.35 给出了改进的上坡挡位决策在实车测试的动态性能。如图4.34所示，62 s时车速已经超过了当前升挡点对应车速（11%油门开度，8.83 m／s），但是由于估计出的广义道路阻力系数平均值大于对应挡位和油门开度下的顺序升挡广义道路阻力系数阈值0.01，所以车辆保持5 挡运行。如图4.35所示，50.5 s时车速低于当前降挡点对应车速（5% 油门开度，6.9 m／s），考虑到估计出的广义道路阻力系数与对应阈值的对比关系，车辆直接从7 挡跳降至5 挡。

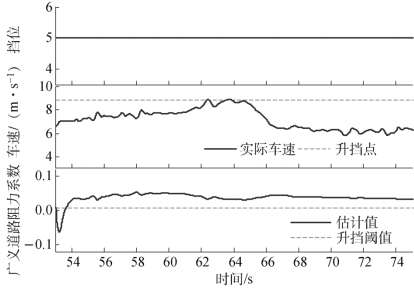
图4.34　实车达到升挡点保持5 挡不变

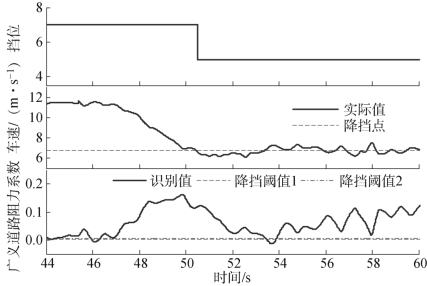
图4.35　实车达到降挡点7 挡跳降5 挡