递推最小二乘法的应用与优势

1.最小二乘法

最小二乘法原本是求解矛盾方程组的一种方法，引入辨识和参数估计领域中可以用来估计差分方程模型的参数。最小二乘法几乎和所有辨识算法有联系，使用时不需要更多的数理统计知识，容易被工程技术人员掌握。当其他算法失效时，有时候最小二乘法仍然可以应用。其具有利于实现递推计算的优点，便于进行数据的成批处理，相对于其他算法计算简单，因此最小二乘法是系统辨识领域应用最广的参数估计方法，也是获取系统数据最佳函数匹配最常用的方法。

对于一个n 阶的滑动平均（moving average，MA）数学模型，可以写成

式中，输出y（t）和输入u（t），u（t－1），…，u（t－n）均由测量得到，而参数b0，b1，…，bn 为待估计的未知量，总共有n +1 个参数需要确定。用矩阵来表示MA 模型，如式（4.15）所示。

其中

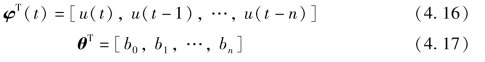
如果选定的模型结构和阶数是正确的，测量所得到的数据又不含任何噪声，那么未知量的估计其实就是n+1 元一次确定性方程组的求解问题。这只需要经过n+1 次对数据y 和u 的测量即可求解出上述的未知参数，将所有n+1 个方程列出，表示为

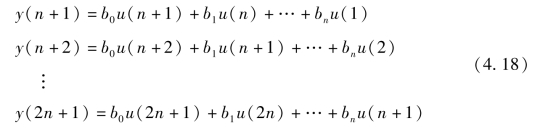
将式（4.18）写成矩阵形式

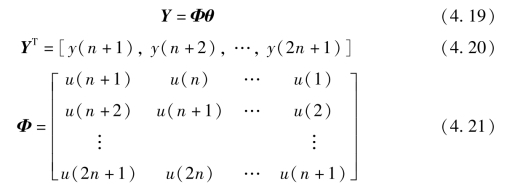
式中，Y 为输出向量；Φ 为观测矩阵；θ 为参数向量。然而，实际的模型中不可能如式（4.18）一样简单，观测矩阵和输出向量中元素的测量难免含有噪声，一旦引入噪声信号，式（4.19）将变为矛盾方程组。为此，在式（4.19）中考虑误差向量E，将系统的模型改为MA 差分模型，如下所示。

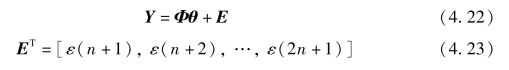
那么，模型的残差为

根据最小二乘法原理，所求未知参数的估计值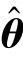（t）使得残差的平方和最小。其性能指标函数如下，其中N 为测量总次数，一般N≫n+1。

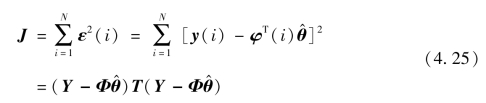
使J 取得最小值的θ 便是待估参数的最小二乘估计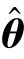（t），估计值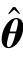（t）由下式导出：(www.xing528.com)

进而得出估计参数的表达式（4.27），只要矩阵ΦTΦ 非奇异，该估计有解。

2.递推最小二乘法及其扩展

式（4.27）给出了最小二乘法估计的一般形式，在车辆参数估计中需要的是对未知参数的实时计算，因此在计算机上实现最小二乘法的递推计算十分重要。最小二乘法的递推计算已经被大量应用，其更新形式基本是标准的。在此直接给出RLS 算法的表达式

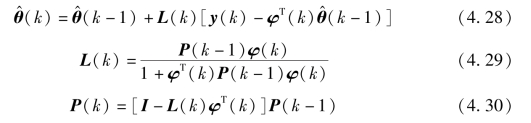
式中，k 为递推计算的步骤数；P（k）为协方差矩阵；L（k）为增益矩阵。

RLS 算法流程如图4.22所示，其中第一个步骤赋初始值是分别对未知估计量θ（0）、协方差矩阵P（0）进行设定，第一次计算前先根据设定的初始值计算增益矩阵L（1），随后计算θ（1）与P（1），此后再利用求出的协方差矩阵更新增益矩阵，进而通过递推计算，求出所有待估参数并输出。

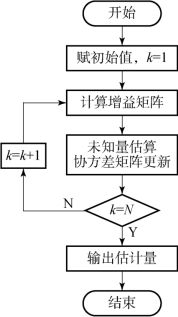
图4.22　RLS 算法流程

当未知参数保持不变时，式（4.28）～式（4.30）能够简单有效地估计出未知参数，然而车辆参数估计值不能保证待估参数为常量，使用上述方法可能会导致数据饱和，每一次递推计算的估计误差会随着数据的增多而加大，常规的RLS 方法将会丧失对参数的估计能力。对此，引入时变参数估计的指数加权最小二乘法——带遗忘因子的RLS，类似于加权RLS 的处理方式，采用遗忘因子对采集到的数据进行加权处理，即在性能指标函数中对被求和的每一项乘一个指数加权系数λk－i，0 ＜λ≤1。那么改进后性能指标函数变为

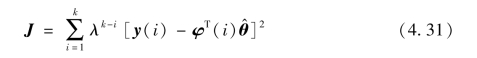
据此推导出未知参数的估计表达式如下，引入遗忘因子后仅协方差矩阵和增益矩阵有所变化。遗忘因子的引入实质上是对所采集数据的加权，随着采样时刻的推移，较先采集的数据权重越来越小，从而逐步被“遗忘”，有利于新采集数据在识别估算中发挥作用，及时反映数据变化对参数估计的影响。

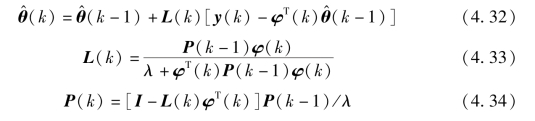
然而，需要同时估计多个未知参数时，如果各个待估参数的变化速率差距很大，那么单一的遗忘因子显然不能满足对这些时变参数的有效识别，因此在待估参数个数不多时，可以考虑针对不同的待估参数分别引入不同的遗忘因子，这种方法称为带遗忘矢量的RLS 或带多遗忘因子的RLS。以两个待估参数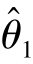（k）、（k）的RLS 估计为例，分别引入两个不同遗忘因子λ1、λ2，那么两个待估参数的表达式如下：

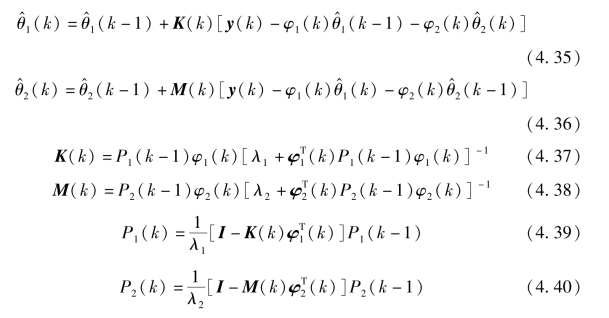
进一步，有学者提出对于带遗忘因子的RLS 识别效果易受遗忘因子取值影响，其值越小，则对时变参数的跟踪能力就越强，但同时对噪声越敏感；遗忘因子取值越大，则跟踪能力随之减弱，但对噪声不敏感，收敛时的参数估计误差也越小。因而选用时变遗忘因子来解决待估参数变化率随时间变化的问题。对于某一个遗忘因子，其时变表达式为

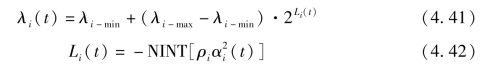
式中，λi－max 和λi－min 为允许的遗忘因子最大、最小取值；NINT 为接近于的最小整数；ρi 为遗忘因子λi 的敏感增益，控制遗忘因子趋近于1 的速率；αi 为估计误差。将上述时变遗忘因子的表达式引入式 （4.35）～式（4.40）中，即可实现对两个不同变化速率的未知参数识别估计。