传动系统动力学模型优化

在对系统进行建模分析之前，需要对动力传动系统进行基本的假设。

（1）忽略发动机扭振、轴的扭振和离合器扭转减震器对系统的影响。

（2）忽略轴的横向振动。

（3）将各元件视为完全刚性无阻尼的惯性元件，并以集中质量的形式表示。

（4）忽略齿轮的啮合间隙，不考虑齿轮啮合时的刚度变化，以综合刚度表示齿轮的啮合刚度。

（5）忽略系统其他运动副的间隙。

（6）除离合器和同步器的摩擦力外，忽略轴承和轴承座之间的摩擦阻力、搅油阻力等系统其他运动副的摩擦阻力。

（7）假定车轮与地面间接触良好，无滑转和滑移。

根据车辆动力传动系统的结构特点，在以上假设的条件下，将其简化为发动机、离合器、变速器及动力输出四个模块，正常运转情况下的动力传动系统基本模型如图2.6所示。

图2.6　正常运转情况下的动力传动系统基本模型

图2.6 中，T2 为变速器输出扭矩，N·m；Tr 为地面阻力矩，N·m；ωe为发动机曲轴转动角速度，即离合器主动部分转动角速度，rad／s；ω1 为离合器从动部分转动角速度，即变速器输入轴转动角速度，rad／s；ω2 为变速器输出轴转动角速度，rad／s；ωr 为驱动轮转动角速度，rad／s；Io 为离合器从动部分、与变速器相连的整车惯量换算到变速器输入轴上的转动惯量，kg·m2；i1 为中间轴和输入轴常啮合齿轮的传动比；iX 为挡位齿轮的传动比；iG／D为副变速器的传动比；io 为主减速器和轮边减速器的总传动比。其余参数含义同前。

图2.6 中的变速器由两部分组成：主变速器和副变速器，两个变速器分段式配成10 个挡位：R （倒）挡、C （爬）挡、1 ～8 挡，其中主变速器部分的1 ～4 挡的变换采用同步器式换挡，R 挡和C 挡的变换采用结合齿套式换挡；副变速器主要是由一组行星齿轮构成高、低两个挡位，配合主变速器实现1 ～8 挡的变换，高低挡的切换同样采用同步器式换挡机构。

R 挡和C 挡都是起步挡，挂入起步挡前，只需要离合器彻底分离，并且等变速器输入轴转速降至较低时，即可进行换挡，对车辆的连续行驶没有影响，因此这里不对R 挡和C 挡的结合齿套式换挡做深入的讨论，下文只针对同步器式换挡过程进行研究。

变速器的换挡过程根据不同的换挡需求分为两种情况：“主变速器换挡”和“副变速器换挡+主变速器换挡”，前者多为普通的连续升、降挡过程，后者则是在4、5 挡之间换挡或跨越4、5 挡的跳挡。

1.主变速器换挡过程动力学模型

车辆在某一挡位行驶时，变速器传动比ig 为

式中，ig 为某一挡位的传动比，其余各变量含义同前。

整个传动系统被简化为一个刚体处理，传动系统的动力学平衡方程式如下：

式中，η 为传动效率，其余各变量含义同前。

主变速器换挡期间，变速器被简化为两个部分：一个是与离合器从动部分相连的输入轴部分，另一个是与分动箱、传动轴等相连的输出轴部分，其升档模型如图2.7所示。

图2.7　主变速器升挡模型

图2.7 中，Ts1为同步器作用在输入轴部分的摩擦力矩，N·m；Ts2为同步器作用在输出轴部分的摩擦力矩，N·m，Ts2与Ts1大小相等，方向相反；Ti为轴承摩擦、搅油损失等效到变速器输入轴上的阻力矩，N·m；I1 为离合器从动盘、一轴齿轮、中间轴齿轮及各挡位的常啮合齿轮等换算到变速器输入轴上的转动惯量，kg·m2；I2 为与变速器输出轴相连的整车惯量等效到变速器输出轴上的转动惯量，kg·m2；其余各变量含义同前。

变速器从低挡升至X 挡时，变速器输入轴部分和输出轴部分的动力学平衡方程式如下：

车辆运行时等效至输出轴的阻力矩为滚动阻力Ff、空气阻力Fw、坡道阻力Fi 和加速阻力Fj 共同作用在车轮上的阻力矩：

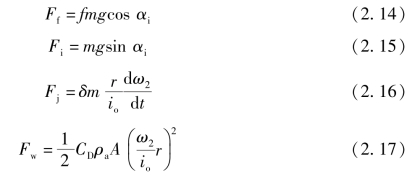
式中，式中，r 为车轮半径，m；f 为滚动阻力系数；m 为整车质量，kg；αi 为道路坡度角；CD 为空气阻力系数；ρa 为空气密度，kg／m3；A 为迎风面积，m2；δ 为车辆旋转质量换算系数。

主变速器降挡模型如图2.8所示。

图2.8　主变速器降挡模型

变速器从高挡降至X 挡时，变速器输入轴部分和输出轴部分的动力学平衡方程式如下：

综合式（2.11）及式（2.18），得到主变速器换挡同步过程中与输入轴相连部分的动力学方程式：

式中，升挡时K ＝1，降挡时K ＝－1。

主变速器的换挡过程研究，主要是针对同步过程，由于变速器输入轴部分的受力较为简单，故而一般将变速器的输入轴部分作为研究对象。

换挡前后变速器输入轴部分的动能变化量ΔW动为

式中，ω′1 为换挡结束后的变速器输入轴转动角速度，rad／s。

同步过程中，作用在变速器输入轴部分上用于改变其动能的功率及同步器摩擦功率的计算公式为

式中，iG／D，X为目标挡位副变速器的传动比。

在普通路况下，同步过程时间短暂，在此期间车速变化较小，一般认为变速器输出轴转动角速度ω2 在同步过程前后相同，同时也可以认为Ts 和Ti是固定值。则同步器的摩擦功可通过下式进行计算：

将P动、P摩、ω2 等参量代入，推导得

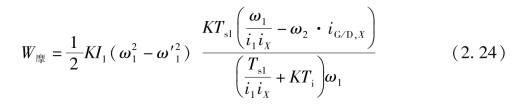
如换挡只在主变速器部分进行，则可以进一步推导得

式中，i当前为当前挡齿轮副的传动比。(www.xing528.com)

由式（2.25）可知，在换挡同步过程中：首先，同步器的摩擦功与换挡时的变速器输入转动角速度ω1 即换挡点有关，换挡点越高，则换挡时的同步器摩擦功越大；其次，同步器的摩擦功和当前挡与目标挡的传动比阶比iX／i当前相关，传动比阶比越大，则摩擦功越大；最后，作用在变速器输入轴部分的阻力矩，也会影响同步器的摩擦功，升挡时K ＝1，阻力矩有利于换挡，降挡时则相反。

在越野路面条件下，车辆滚动阻力较大，变速器输出轴转动角速度ω2 在同步过程前后的变化不能被忽略，因此同步器的摩擦功需要通过对摩擦功率的积分计算获得，如下式：

式中，t4 为同步时间，s。

根据式（2.22）可知，升挡时，在同步过程中如果输出轴转动角速度ω2增加，则摩擦功率减小，同时有利于缩短同步时间，减小换挡过程中同步器摩擦功；如果输出轴转动角速度ω2 减小，则摩擦功率增加，同时会延长同步时间，增加换挡过程中同步器的摩擦功。降挡时则情况刚好相反。

2.副变速器换挡过程动力学模型

副变速器换挡期间，为减少副变速器同步过程的同步惯量，降低同步难度，主变速器一般处于空挡位置，变速器被简化为三个部分：与离合器从动盘相连的主变速器一轴部分、主变速器的二轴部分和与分动箱传动轴相连的副变速器的输出轴部分，其模型如图2.9所示。

图2.9　副变速器升挡模型

图2.9 中，Ti2为轴承摩擦、搅油损失等效到主变速器二轴上的力矩，N·m；Ts3为副变速器同步器作用在二轴部分的摩擦力矩，N·m；Ts4为副变速器同步器作用在输出轴部分的摩擦力矩，N·m；I副为与二轴相连的挡位齿轮、行星排等换算到二轴上的转动惯量，kg·m2；I3 为与副变速器输出轴相连的整车惯量等换算到变速器输出轴上的转动惯量，kg·m2；ω副为主变速器二轴的转动角速度，rad／s；其余各变量含义同上。

升挡时，副变速器同步器主、从动部分的动力学平衡方程式如下：

副变速器换挡时，由于主变速器先换至空挡，因此主变速器上与一轴相连的离合器摩擦片、中间轴等转动惯量均不对副变速器的换挡过程造成影响，副变速器的换挡过程只影响主变速器的二轴及与其相连的挡位齿轮和副变速器的行星排等，其转动惯量较小，同步过程较为容易实现。

以本书试验车辆的变速器为例，副变速器采用气动换挡，由换挡气缸简单的充放气动作实现换挡，操纵简便易行，后文对此不做深入的讨论，只将主变速器的换挡过程作为研究的重点。

3.起步过程动力学模型

车辆起步过程动力学简化模型如图2.10所示。车辆起步时已经挂上起步挡，所以动力传动系统被分为两个自由体：发动机动力输出至离合器主动部分、离合器从动部分至驱动轮。

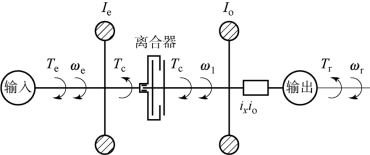
图2.10　车辆起步过程动力学简化模型

设以θ（t）为变量的二自由体运动方程的矩阵形式为

式中，I，C 和K 分别为系统惯性矩阵、阻尼矩阵和刚度矩阵；（t），（t）和θ（t）分别为角加速度、角速度和角位移向量；Md（t）和Ml（t）分别驱动扭矩向量和负载扭矩向量。

根据建模假设，其阻尼矩阵和刚度矩阵为O，因而可以把式（2.29）简化为

式中，（t）＝（t）。

式（2.30）是典型的集中转动惯量的运动方程。

根据式（2.30）分别对图2.10 的车辆动力传动系统简化模型进行分析。

1）发动机至离合器主动部分

对于这部分的构件，发动机的有效输出扭矩Te 为其驱动扭矩，离合器的传递扭矩Tc 为其阻力矩。根据式（2.30）有

2）离合器从动部分至驱动轮

对于这部分构件，离合器所传递的扭矩Tc 为其驱动扭矩，Tr 为驱动轮所受的地面阻力矩。根据式（2.30）有

式（2.31）～式（2.34）组成了动力传动系统模型的基本公式，可以把其用矩阵表示如下：

离合器从开始接合到接合完成的过程可分为三个阶段：无扭矩传递阶段、滑摩阶段和同步阶段，其中滑摩阶段可再分为两个阶段。以上四个阶段的具体情况如下。

（1）无扭矩传递阶段。用于消除离合器主、从动部分的间隙，此阶段：

式中，j 为冲击度，m／s3。

离合器主、从动部分未接合，离合器未传递扭矩，因而不存在冲击，只有当离合器主、从动部分间隙消除后，离合器才会传递扭矩。

（2）滑摩阶段前半段。有扭矩传递但无车速，此时两个自由体的动力学方程分别为

此阶段离合器主、从动部分开始滑摩，但其所传递的扭矩Tc（t）不足以克服阻力矩Tr（t），使车辆移动。

（3）滑摩阶段后半段。离合器继续滑摩，有扭矩传递，车辆出现速度和加速度，此时两个自由体的动力学方程分别为

式中，kg 为计算系数。

可见，此阶段存在冲击，并且与离合器传递扭矩Tc（t）的变化率相关。

（4）同步阶段。此时离合器主、从动部分的滑摩结束，有关系式：

可见，同步阶段的冲击度的大小与发动机输出扭矩的变化率相关。

车辆的纵向冲击度决定了乘员的乘坐舒适性，是起步过程的一个重要控制目标。结合上文中起步过程冲击度的计算公式可知，冲击度出现在滑摩阶段后半段和同步阶段。

在无扭矩传递阶段和滑摩阶段的承接点处，是离合器输出扭矩从无到有的过程，如果离合器输出摩擦扭矩变化较快，即离合器接合速度较快，则容易导致较大的冲击，此处是起步过程控制的第一个关键点。为避免在无扭矩传递阶段和滑摩阶段的承接点处产生较大的冲击度，则需要控制离合器在滑摩阶段初始时刻的接合速度，减缓离合器输出摩擦扭矩的变化率。

通过上文的公式推导可知，滑摩阶段离合器输出的摩擦扭矩由离合器主、从动部分的压紧力决定，而同步阶段离合器输出的扭矩由发动机输出扭矩决定，因此在滑摩阶段和同步阶段的承接点处，即离合器的同步点处，会由于离合器输出扭矩的剧烈变化而导致较大的冲击，此处是起步过程控制的第二关键点，这也在实车试验中得到了验证。为降低离合器同步点处的冲击度，则需要滑摩阶段后半段的离合器输出摩擦扭矩不能超过发动机输出扭矩太多，这是控制离合器同步点处冲击度的有效方法。