锌的热力学特性

1.热容

金属锌的气态分子由单原子所组成。所有单原子气体的热容都有如下的数值：

摩尔定容热容：C_V，m=12.56J/（K·mol） （2-1）

摩尔定压热容：C_p，m=C_V，m+R=20.87J/（K·mol） （2-2）

C_p，m的精确值为20.80J/（K·mol）。升温时系统所吸收的热量全部用来增加分子移动的动能，并且遵循能量均分原则平均地分配在三个不同的方向上（三个自由度）。

气态锌的热容与所有金属蒸气的热容一样，其数值都具有不随温度变化而变化的特点。

气态锌的原子是以无规律的形式运动着的，加热的结果仅仅是增大了它们的动能。而液态的锌原子在近距离范围内具有规则的点阵结构，这种有秩序的排列方式只有在达到较远距离时才会逐渐消失。由于质点间的相互作用，升温的结果不仅增大了原子或离子的振动动能，同时也增大了它们的位能。

液态锌热容具有两个特点：

1）在熔点附近的热容与固态非常相似。锌在692.5K（419℃）时有：

C_V，m（固态）=29.80J/（K·mol） （2-3）

C_p，m（液态）=32.78J/（K·mol） （2-4）两者的差值仅约为3J/（K·mol）。

2）液态锌的C_p，m值随着温度的升高而逐步下降，见表2-2。热容的变化有一定的规律，大致温度每升高100K，C_p，m数值减少0.8J/（K·mol）左右。

对于固体金属，随着温度的升高，C_p，m值将会逐步增大。在达到第一个转变点（第一次相变点或熔点）时，C_p，m的最大值通常可以增大到29～33J/（K·mol）。对所有元素来说，这个最大值几乎是相同或相近的。

表2-2 液态锌摩尔定压热容C_p，m和温度的关系

固态锌在室温298K（25℃）下的摩尔定压热容为25.35J/（K·mol），而在第一个相变点即熔点时的C_p，m值为29.80J/（K·mol）。

固态锌的摩尔定压热容和温度的关系式如下：

C_p，m=21.98+1.13×10^-2T （273～693K） （2-5）

或 C_p，m=22.40+1.00×10^-2T （298～692.5K） （2-6）

根据上述关系式所得的计算结果，其精度可以达到±1%。表2-3是根据关系式计算得到的固态锌在某些温度下的C_p，m值。

表2-3 固态锌在某些温度下的C_p，m值

2.熵

熔化热的大小与金属键的强度有关。金属键的强度越大，相应的熔点就越高，熔化热也就越大。这是因为熔化时所提供的能量应足于破坏金属长程有序的晶格点阵。

熔化温度（K）除熔化热称为熔化熵，即金属在熔化时的熵增ΔS_f。对绝大多数金属来说，尽管熔化热各不相同，但它们的熔化熵却非常接近，一般为9.6～10.0J/（K·mol）。锌的熔化热为6700J/mol，熔化熵为9.65J/（K·mol）。

汽化热的大小也与金属键的强度有关。金属键越强，拆散金属晶格所需的能量就越大，即汽化热就越大，沸点也就越高。汽化热与沸点之间的比值接近于一个常数，这一规则称为特鲁顿规则，这个常数就是汽化熵。锌在沸点（1180K）的汽化熵为97.32J/（K·mol）。

锌在固、液、气态的熵与温度的关系式如下：(www.xing528.com)

固态锌：S⁰_T=-86.88+50.62lgT+1.13×10^-2T（273～692.5K）（2-7）

液态锌：S⁰_T=-137.70+73.18lgT+2.30×10^-3T（2-8）

气态锌：S⁰_T=-40.11+47.94lgT（2-9）

3.蒸气压

蒸气压是金属锌的一项极为重要的热力学数据，锌的一系列物理化学性质都由这个参数所规定。

锌的蒸气压随温度的升高而增大。蒸气压和温度的关系服从指数规律，即蒸气压的增长速度最初很缓慢，当达到约1023K时急剧增大。

液态锌或固态锌与其蒸气共处时属于单组分两相系统。根据相律，这样的系统只有一个自由度，即在一定的温度下只有唯一的、确定的平衡蒸气压与之对应。

液态锌的蒸气压常用Kelley方程计算：

lgp=-6754.5T^-1-1.318lgT-6.01×10^-5T+9.843（2-10）

固态锌的蒸气压则用Barrow-Dodsworth方程计算：

lgp=9.8253-0.1923lgT-0.2623×10^-3T-6862.5T^-1（2-11）在式（2-10）和式（2-11）中，p的单位为atm（1atm=101325Pa）。

在各种不同的温度下，由Kelley方程计算得到的蒸气压数值与实测值非常接近，见表2-4。

表2-4 液态锌的饱和蒸气压

（续）

4.表面张力

表面张力和金属的原子结构有一定的关系。液态金属的表面张力是液体内部质点与表层质点相互作用的内聚力没有达到平衡而产生的。内聚力越大，或者说不平衡的程度越大，相应地表面张力也就越大。

内聚力就是物体内部质点间的相互作用力。对各种金属来说也就是金属键的强度，即原子核和自由电子间的引力。因此，从理论上说，金属的表面张力和它们的熔点、沸点、熔化热及汽化热之间存在着某种对应关系。

金属的表面张力一般都随着温度的升高而下降，这是金属键被削弱了的缘故。液态锌在783K（510℃）时，其表面张力为0.785N/m；当温度上升到913K（640℃）时，它的表面张力则下降为0.761N/m。

表面张力在热浸镀锌中具有实际意义。在热浸镀锌过程中，降低液态锌的表面张力，有助于增加锌液对钢铁表面的润湿性，减少漏镀的发生。液态锌的表面张力除了与温度有关外，还与第二组元的加入有关，因此，可通过改变锌浴温度和在锌浴中添加微量合金元素来达到改变锌浴的表面张力。

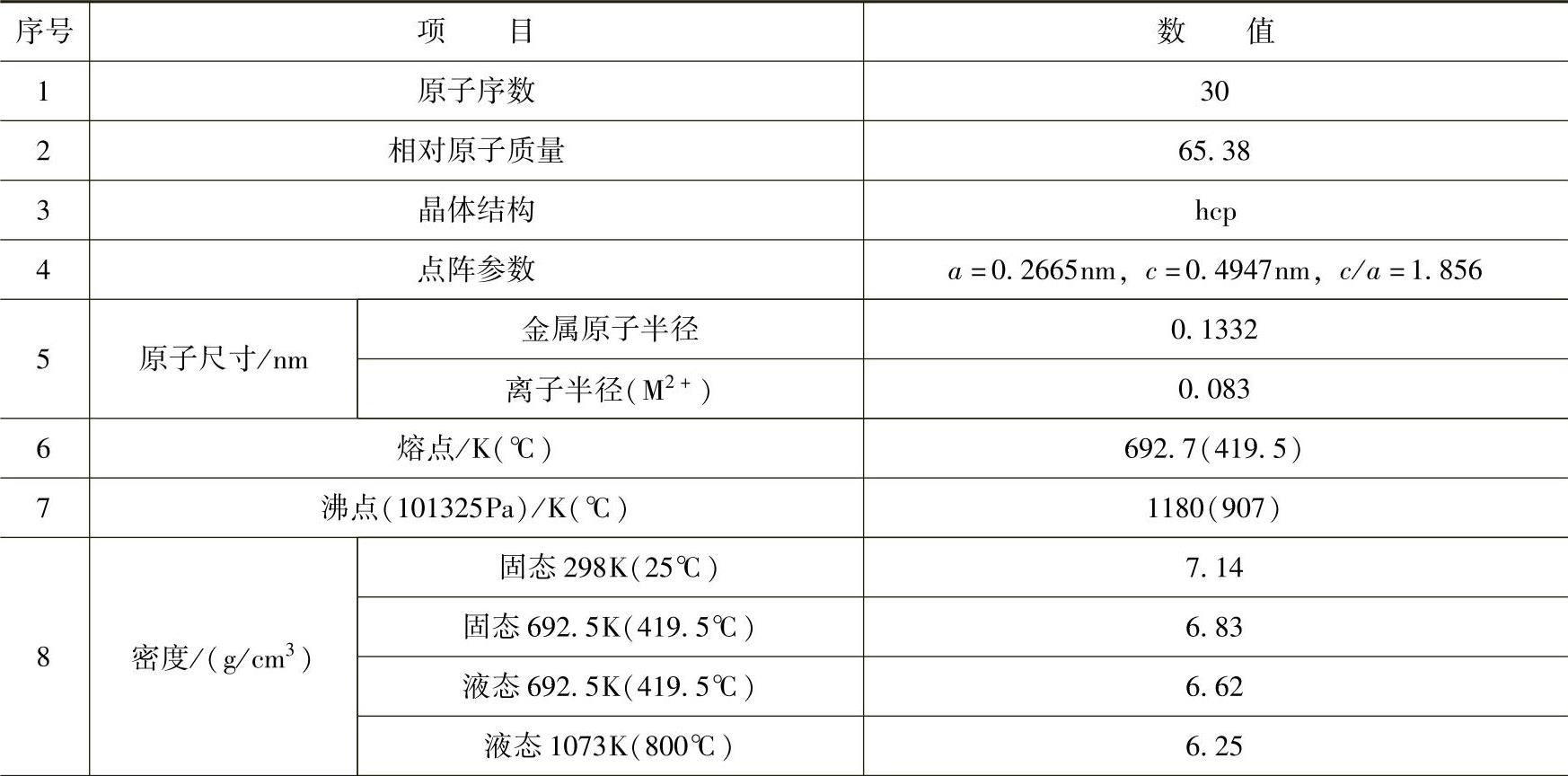
表2-5列出了锌的物理化学参数。

表2-5 锌的物理化学参数

（续）