如何计算以轨条砦为目标的破障任务终点毁伤效能？

基于以上方法和模型，以某破障火箭弹为例，威力场半径为7 m，CEP＝20 m，打击方案选择双瞄点打击，选取y 轴两侧面积相同的矩形的几何中心为瞄点，瞄点坐标分别为A1（-7.875，0），A2（7.875，0），如前文图2 所示。针对所构建的以轨条砦组成的反登陆目标区域执行破障任务时的终点毁伤效能进行计算分析。

分别计算了在达到相同概率时，毁伤不同比例轨条砦目标所需的用弹量以及在期望概率不同时，毁伤相同比例的轨条砦所需的用弹量，针对毁伤比例80%、90%和100%时用弹量-期望概率曲线，以及期望概率85%、90%和95%时用弹量-毁伤比例曲线进行了对比分析。

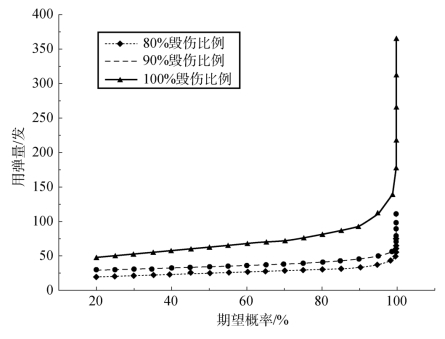
由图4 可以看出，在毁伤比例相同时，用弹量随着期望概率的增加而增大。在期望概率小于95%时，用弹量随期望概率的增加较为平缓，随着期望概率趋近100%，所需用弹量急剧增大，根据曲线趋势，可以预测，当概率无限趋近100%时，所需用弹量也趋于无穷。上述计算结果表明，无论是理论上数学概率统计计算还是工程上的毁伤效能评估计算，概率上的无限趋近100%都是很难实现的。当期望概率趋近100%时，用来衡量终点毁伤效能的指标-用弹量的大小就仅存在数学层面的意义，其结果对于工程上毁伤效能评估的价值意义很小。因此，在火箭弹对集群目标的终点毁伤效能评估中，应基于合理的数学概率理论以及预期作战任务的背景，提出合理的期望毁伤概率。

达到相同期望概率条件下，毁伤比例越高，所需的用弹量也会有明显增加，且在相同期望概率时，毁伤比例80%和毁伤比例90%两种条件下用弹量相差不大，达到100%毁伤比例的用弹量明显高于前两者。

(www.xing528.com)

图4　用弹量与期望概率关系曲线

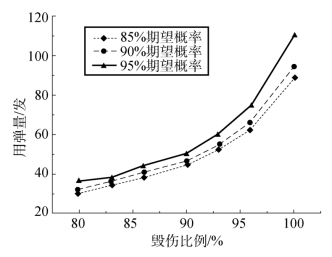
图5　用弹量与毁伤比例关系曲线

由图5 可以看出，在相同期望概率时，用弹量与毁伤比例成正相关，随着毁伤比例越大，所需用弹量越多，且增幅也不断增大。在达到100%毁伤比例时，所需用弹量远远大于毁伤80%时的用弹量；在相同毁伤比例时，期望概率越大，所需用弹量越大，所得规律与图1 所述相同。基于以上数据规律，可以看出，在打击由离散独立目标组成的集群目标时，全部毁伤（毁伤比例100%）所需代价条件相对较大。对于破障任务来说，战术预期是开辟一定宽度的通路，所以，在破障火箭弹的终点毁伤效能评估中，选择80%～95%区间内的毁伤比例具有较高的工程参考价值。

综合来看，除了得到评估模型中最基本的规律性认识，也可以通过数据规律看出，对于压制类武器打击集群目标时，达到数量上100%毁伤所需用弹量相对难以接受，在实战中资源消耗巨大，不具有可操作性。另一方面，基于蒙特卡洛方法的毁伤评估模型决定了期望概率达到100%在数理上无法实现，在实际作战中，也无法做到100%战术行动的成功。计算结果符合理论预期，可以验证所建立的评估模型的合理性。