数值修约原则及实施规范

在测量中，由于存在测量误差，测得值只能是被测量的真值的近似值，因此，在一般情况下，对于一个正确的测量数值，只允许其最后一位数字是可疑的或不可靠的。

1.术语和定义

（1）数值修约 通过省略原数值的最后若干位数字，调整所保留的末位数字，使最后所得到的值最接近原数值的过程，称为数值修约。经数值修约后的数值称为（原数值的）修约值。

（2）修约间隔 修约间隔是指修约值的最小数值单位。修约间隔的数值一经确定，修约值即为该数值的整数倍。

例1：如指定修约间隔为0.1，修约值应在0.1的整数倍中选取，相当于将数值修约到一位小数。

例2：如指定修约间隔为100，修约值应在100的整数倍中选取，相当于将数值修约到“百”数位。

2.数值修约规则

（1）确定修约间隔

1）指定修约间隔为10^-n（n为正整数），或指明将数值修约到n位小数。

2）指定修约间隔为1，或指明将数值修约到“个”数位。

3）指定修约间隔为10ⁿ（n为正整数），或指明将数值修约到10n数位，或指明将数值修约到“十”“百”“千”……数位。

（2）进舍规则 用一句话说：一般均采用“四舍六入五单双奇进偶退”法来选取，其一般规则如下：

1）拟舍弃数字的最左一位数字小于5，则舍去，保留其余各位数字不变。

例：将12.1498修约到个数位，得12；将12.1498修约到一位小数，得12.1。

2）拟舍弃数字的最左一位数字大于5，则进一，即保留数字的末位数字加1。

例：将1268修约到“百”数位，得13×10²（特定场合可写为1300）。“特定场合”是指修约间隔明确时。

3）拟舍弃数字的最左一位数字是5，且其后有非0数字时进一，即保留数字的末位数字加1。

例：将10.5002修约到个数位，得11。

4）拟舍弃数字的最左一位数字为5，且其后无数字或皆为0时，若所保留的末位数字为奇数（1，3，5，7，9）则进一，即保留数字的末位数字加1；若所保留的末位数字为偶数（0，2，4，6，8），则舍去。

例1：修约间隔为0.1（或10^-1）。

拟修约数值 修约值

1.050 10×10^-1（特定场合可写成为1.0）

0.35 4×10^-1（特定场合可写成为0.4）

例2：修约间隔为1000（或10³）。

拟修约数值 修约值

2500 2×10³（特定场合可写成为2000）(www.xing528.com)

3500 4×10³（特定场合可写成为4000）

5）负数修约时，先将它的绝对值按上述规定进行修约，然后在所得值前面加上负号。

例1：将下列数字修约到“十”数位。

拟修约数值 修约值

-355 -36×10（特定场合可写为-360）

-325 -32×10（特定场合可写为-320）

例2：将下列数字修约到三位小数，即修约间隔为10^-3。

拟修约数值 修约值

-0.0365 -36×10^-3（特定场合可写为-0.036）

6）不允许连续修约。

①拟修约数字应在确定修约间隔或指定修约数位后一次修约获得结果，不得多次按上述规则连续修约。

②在具体实施中，有时测试与计算部门先将获得数值按指定的修约数位多一位或几位报出，而后由其他部门判定。

3.计算法则

（1）加减运算 在加减运算中，参与运算的数据保留的小数位数，要比小数位数最少的那个数多保留一位。在计算结果里，应保留的小数位数和小数位数最少的那个数的位数相同。

（2）乘除运算 在乘除运算中，参与运算的数据，以有效位数为准，其余数据可多保留一位。计算结果的有效位数，应与有效位数最少的那个数相同。

（3）乘方、开方运算 在乘方、开方运算中，计算结果的有效位数，应与原始数据相同。

（4）某些数字常数 如π、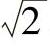、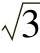等，在参与运算时，也按上述方法确定其有效位数，但为了保证最终运算结果的准确度，可适当多取1或2位。

4.修约的目的

一般情况下，对于一个正确的测量数据，只允许其最后一位数字是可疑的或不可靠的；并不是一个数值小数点后的位数越多，这个数就越准确；也不是在测量过程中，测量结果中保留的位数越多就越准确。位数的多少虽与测量仪器读数有关，但是数值小数点的位置仅与所用单位大小有关，不是决定准确度的标志。

例如，一个重物的质量为64.52kg，可以写作0.06452t或64520g。无论写多少位数，绝对不能把准确度提高到超过仪器的精度。

正确的写法应该是：除最后一位数字是可疑的、不准确的或不可靠的外，其余各位数字都应该是准确的、知道的。

例如，用分度值为0.01mm，规格为75～100mm的外径千分尺测量某零件底板的高度（80±0.02）mm，有的人可能读为80.025mm，有的人读为80.023mm，有的人读为80.027mm；而80.02这个数字是准确的，最后一位数字5、3、7是估读的，或是可疑的。

一般认为，最后一位数字上下可能有一个单位的出入。其绝对误差不大于末位数上的半个单位。

由此可见：测量过程中读数必须进行修约；同时在检测中，出现靠近合格界限的边缘数据时，须进行必要的重复检测，以验证检测的准确性；做好检测原始记录。当检测由一人读数、一人记录时，记录人员要复念一遍所记的数字，以避免数字传递发生差错。