如何进行联合电力系统调频优化？

由于大型电力系统具有许多优点，因而现代电力系统的规模越来越大，出现了几个区域电力系统相互连接起来构成的大型电力系统，即联合电力系统。联合电力系统当然可采用积差调节法对全系统进行调频。但考虑到由于电网容量大，实现起来有困难。如调频厂不位于负荷中心，可能引起联络线上的功率超出允许值，危及系统稳定。因此，可以将联合系统实行分区控制。将每个区域电力系统看成一个区域，每个控制区域的负荷由本区域内的电源和从其他控制区域中经过联络线提供。联络线上交换的功率按一定的约定进行控制，或规定联络线上通过的有功功率的限值，或规定通过的电量的限值，也可以既规定功率限值又规定电量限值等。

为寻求调频规律，先讨论如图5-9（a）中M系统和N系统的频率—交换功率特性。假设交换功率PMN从M系统流向N系统时为正。当M系统负荷增加且N系统负荷不变时，则系统频率下降，M系统和N系统机组要增加出力，使系统频率回升，稳定在略低于原有频率上运行。对负荷不变的N系统来说，使联络线功率PMN减小，即ΔPMN＜0，而频率f有所降低，Δf＜0；对M系统而言，有ΔPMN＜0，Δf＜0。当M系统负荷减小且N系统负荷不变时，两侧系统出力要减小，对负荷不变的N系统来说，有ΔPMN＞0和Δf＞0；对M系统而言，有ΔPMN＞0和Δf＞0。作出负荷不变的N系统的频率—交换功率特性如图5-9（b）所示。同样理由，当M系统的负荷N系统的负荷变化时，作出负荷不变的M系统的频率—交换功率特性如图5-9（b）所示。

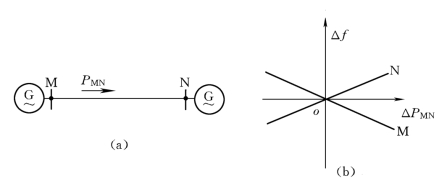
图5-9　联合调频示意图

（a）联合电力系统；（b）频率—交换功率特性

由上述分析可知，M系统或N系统负荷变化时，联络线功率要发生变化，系统频率要发生变化。当另一系统负荷增加时，负荷不变的系统随频率的降低其输出的交换功率将增加。当另一系统负荷减小时，负荷不变的系统随着频率的升高其输出的交换功率将减小。

由图5-9（b）可知，对M系统，ΔPMN与Δf有相反的符号。对N系统，ΔPMN与Δf有相同的符号。则频率—交换功率特性方程式为：

M系统：(www.xing528.com)

N系统：

式中 Δf——频率偏差，Δf=f-fn；

KM、KN——M和N系统频率—交换功率直线特性斜率绝对值。

为了实现分区调频，就要按ΔPMN与Δf来调整，当M系统和N系统按式（5-33）和式（5-34）实现调频时，就能满足本区域系统引起频率偏差时才进行调频的要求，如正常运行时，M系统向N系统输送有功功率，则当M系统负荷增加时而N系统负荷不变时，系统频率要降低，即Δf＜0，同时联络线功率要减小，即ΔPMN＜0。这样，对N系统来说，ΔPMN与Δf关系落在图5-9（b）中第三象限的特性上，自然式（5-34）等式成立，N系统内调频器不动作。对M系统而言，因此进Δf＜0和ΔPMN＜0，式（5-33）不成立，即调频方程的平衡关系破坏，调频器动作，使发电机增加出力。当M系统内机组增加的出力等于负荷增加时，系统频率恢复到额定值，此时，Δf=0、ΔPMN=0，式（5-33）和式（5-34）等式成立，调频器停止动作，联络线中交换功率也保持原有的数值。显然，达到了分区调频的目的。

需要指出，当M系统和N系统的负荷同时变化时，则式（5-33）和式（5-34）的平衡条件同时破坏，M系统和N系统的调频器同时动作，各自调整机组出力，直到式（5-33）和式（5-34）成立时调频才结束。此时有Δf=0、ΔPMN=0，即保持额定频率和联络线交换功率不变。