电力系统负荷的功频特性介绍

当系统频率变化时，整个系统的有功负荷也要随着改变，即

PL=F（f）

这种有功负荷随频率而改变的特性称为负荷的功率——频率特性（简称功频特性），也是负荷的静态频率特性。

电力系统中各种负荷与频率间的关系大致有与频率变化无关的负荷、与频率成正比的负荷、与频率的二次方成比例的负荷、与频率三次方成比例的负荷以及与频率更高次方程比例的负荷。

负荷的功频特性一般可表示为

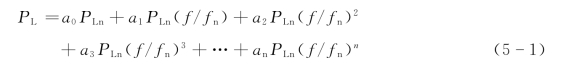
式中 fn——额定频率；

PL——系统频率为f时，整个系统的有功负荷；

PLn——系统频率为额定值fn时，整个系统的有功负荷；

a0，a1，…，an——各类负荷占PLn的比例系数。

若将式（5-1）用标么值形式表示时，则可表示为

显然，当系统频率为额定值时，PL*=1，f*=1，于是有

一般情况下，应用式（5-1）或式（5-2）计算时，通常取到三次方即可，因为系统中与频率高次方成比例的负荷很小，可忽略。(www.xing528.com)

式（5-1）或式（5-2）称为电力系统有功负荷的静态频率特性方程。当系统负荷的组成及性质确定后，负荷频率特性方程也就确定了。因此也可以用曲线来表示，如图5-1所示。

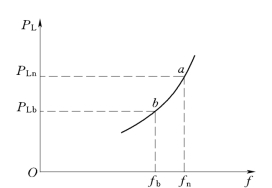
图5-1　负荷的静态频率特性

如图5-1所示，在额定频率fn时，系统负荷功率为PLn，当频率下降到fb时，系统负荷功率由PLn下降到PLb，如果频率升高，负荷功率将增大。也就是说，系统机组输入功率与负荷功率之间失去平衡时，系统中的负荷也参与了调节作用。这种现象称为负荷的频率调节效应。通常用KL*来衡量调节效应的大小，称KL*为负荷的频率调节效应系数。

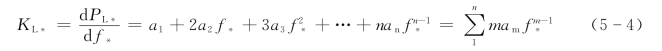
由式（5-4）可知，系统的KL＊值决定于负荷的性质，它与各类负荷所占总负荷的比例有关。

在电力系统运行中，允许频率变化的范围很小，在较小的频率变化范围内，有功负荷与频率的关系曲线接近于直线，如图5-2所示。直线的斜率为

有名值与标么值间的换算关系为

式中 KL*——负荷的频率调节效应系数标么值；

KL——负荷的频率调节效应系数有名值。

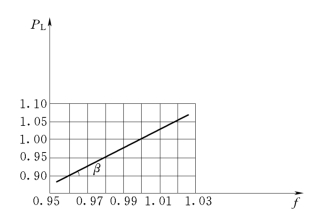
图5-2　有功负荷的静态频率特性