平面与圆球的截交线为圆。由于截平面相对投影面的位置不同,截交线的投影也不同。当截平面垂直、倾斜、平行于投影面时,截交线在该投影面上的投影分别为直线、椭圆和圆(见图8.17)。
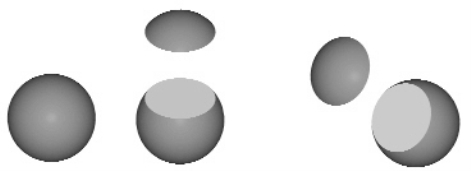
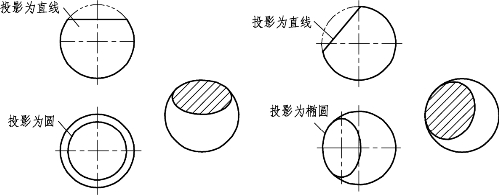
图8.17 球的截交线
例9 如图8.18(a)所示,已知圆球被P、Q两平面截切后的主视图,求作其俯视图和左视图。
解:
(1)分析。
球被水平面P和正垂面Q截切。水平面P与球的截交线圆的水平投影反映实形,其正面投影和侧面投影分别积聚为水平线段。正垂面Q与球的截交线圆的正面投影积聚成直线段,其水平投影和侧面投影均为椭圆。
由于截平面P与Q相交,还应作出其交线EF的投影[见图8.18(b)]。
(2)作图。
①作出完整圆球的俯、左视图[见图8.18(c)]。
②作出水平面P与球的交线——水平圆的水平投影和侧面投影。平面P、Q的交线EF(正垂线)的正面投影e′f′为p′与q′的交点,由此可作出其水平投影ef和侧面投影e″f″[见图
8.18(d)]。
③作出正垂面Q与球的交线。
特殊点:
在主视图中,q′与球的主视图轮廓线相交于点a′和b′,其水平投影a、b和侧面投影a″、b″分别为两个视图中椭圆短轴的端点。其长轴端点的正面投影c′和d′位于a′b′的中点,由此可用纬圆法作出其水平投影c和d(或取cd=a′b′,a′b′为截交线圆的直径,即为椭圆的长轴长度),进而作出侧面投影c″和d″(c″d″=a′b′)[见图8.18(e)]。
从主视图中可看出,G、H为球的俯视图轮廓线上的点,点g′、h′位于q′与水平轴线的交点处,水平投影g、h在球的俯视图轮廓线上,由此可作出其侧面投影g″、h″[见图8.18(f)]。
一般点:
在a′b′线段上定出一些一般点,用纬圆法作出它们的其余投影。(此处略)
用光滑曲线依次将各点连接起来[见图8.18(g)]。(https://www.xing528.com)
④整理。
从主视图上可以看出,位于交线投影e′f′左方的水平圆部分已被正垂面Q截去,位于e′f′上方的椭圆部分也被水平面P截去,这两部分相应的水平投影和侧面投影应画成双点划线或不画。同样,球的俯视图轮廓线的水平投影应只画到点c和d,C和D左端部分的球体已被正垂面Q截去。球的左视图轮廓线的侧面投影应只画到水平面p″,P平面上方的球体也已被截去。
最后检查,描深[见图8.18(h)]。
图8.18(i)为擦去标注和双点划线的三视图。
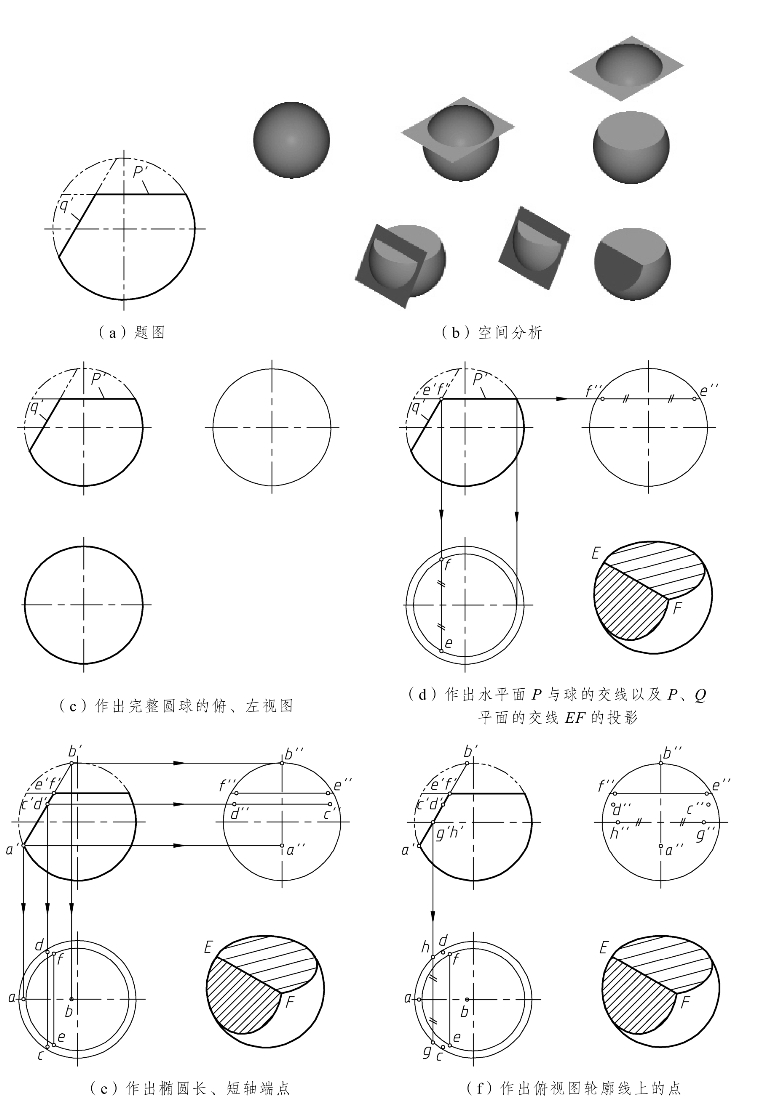
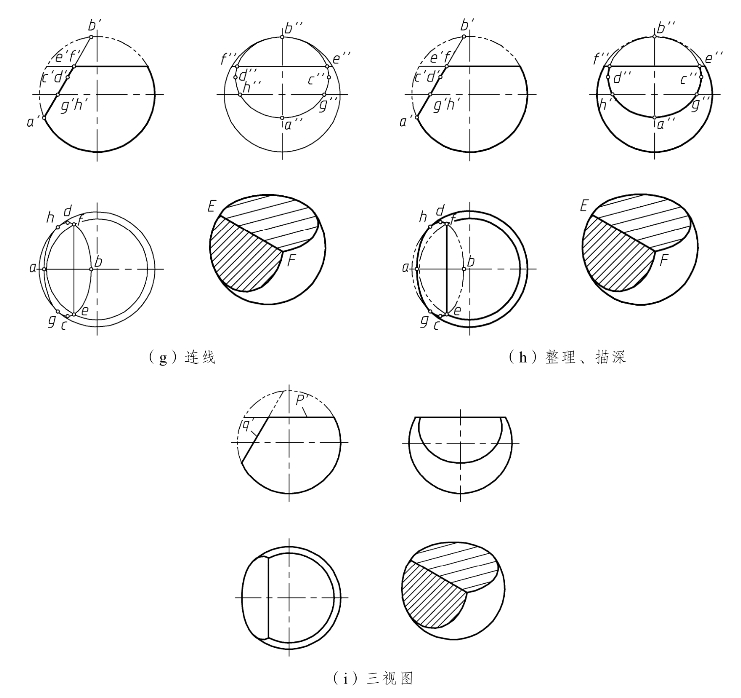
图8.18 例9
例10 如图8.19(a)所示,已知带切口半球的主视图,求作其俯、左视图。
解:
(1)分析。
半球的切口可看作是由一个水平面P和两个侧平面Q、T截切而成。水平面P与半球的交线为水平圆,其水平投影反映圆的实形,另两个投影分别积聚成直线。两个侧平面Q、T与半球的交线为两个侧平半圆,其侧面投影反映半圆的实形,另两个投影分别积聚成直线。由于P、Q、T三个平面并未与球完全相交,因此截交线只是水平圆和侧平半圆的一部分。另外,还需求作水平面P与侧平面Q、T的交线,交线为两条正垂线[见图8.19(b)]。
(2)作图。
①作出完整半球的俯、左视图[见图8.19(c)]。
②作出两侧平面Q、T与半球的交线:在主视图上扩展侧平面Q的正面投影,获取截交线圆弧的半径(长度为a′b′),作出截交线圆弧的水平投影(积聚成左、右两条直线)和侧面投影(重合的圆弧)[见图8.19(d)]。
③作出水平面P与半球的交线:在主视图上扩展水平面P的正面投影,获取截交线圆弧的半径(长度为c′d′),作出截交线圆弧的水平投影(前、后两段圆弧)和侧面投影(积聚成直线)[见图8.19(e)]。
④作出截平面P与Q、T的两条交线EF和GH(正垂线):两条交线的正面投影e′f′、g′h′分别积聚在p′与q′、t′的交点处,其水平投影分别与已作出的侧平圆弧的投影重合,实际上也就是这两个侧平面Q、T的有积聚性的水平投影。由这两条交线的正面投影和水平投影即可作出它们互相重合的侧面投影[见图8.19(f)]。
⑤整理:由于是上半个球,俯视图上的所有投影均可见,画成实线。在左视图上,两条交线的投影因被左半球遮挡而不可见,画成虚线,它们与已作出的两段水平圆弧的侧面投影在同一直线上。水平面P的侧面投影以上的左视图轮廓线应画成双点划线或不画。最后检查、描深[见图8.19(g)]。
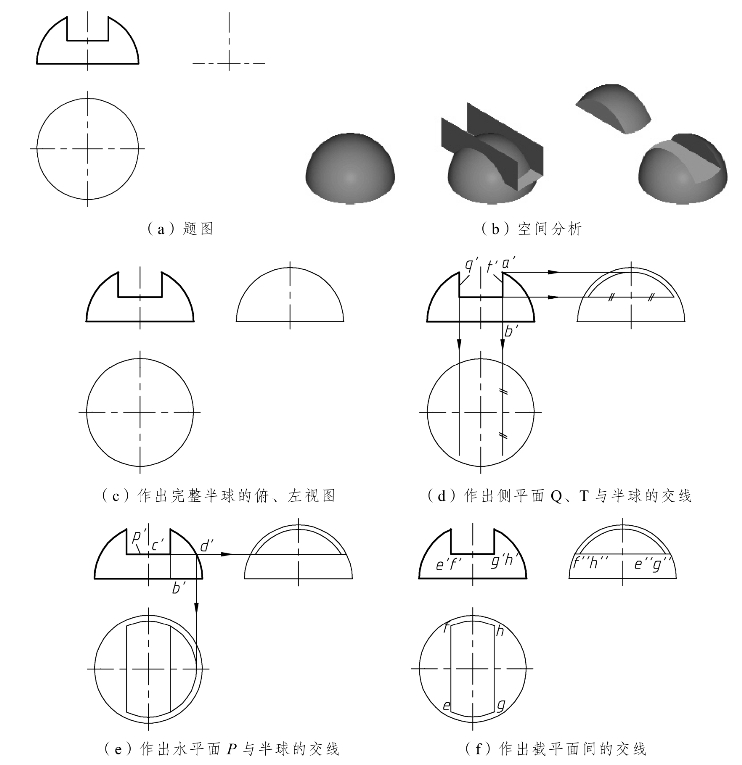
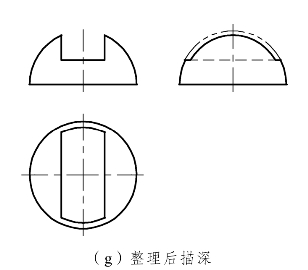
图8.19 例10
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




