相似性度量因子的优化方式

信息熵最初由Hartley提出，假设一条消息由n个符号描述，每个符号有s种不同的可能，这样一条消息共有sn种可能性，其信息量就用sn来度量。为使其线性增加，采用对数形式为:

H=log2sn=nlog2s

(5.1-14)

考虑到实际情况中每种情况的出现概率是不同的，用概率来衡量每种可能性，则信息量由其概率加权得到。例如，某一随机事件共有n种可能，其概率分别为p1，p2，…，pn，则Shannon熵定义为:

(5.1-15)

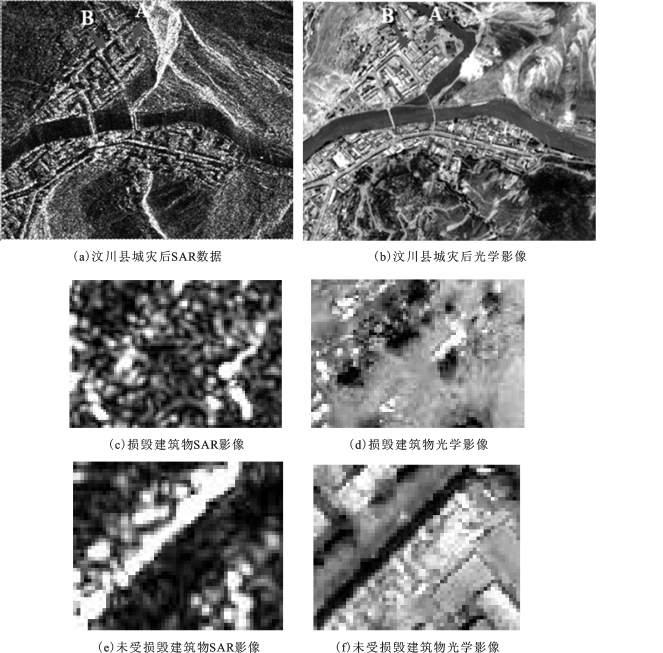
图5.10　汶川地震中汶川县城震后SAR影像与光学影像对比图

Shannon熵具有3种含义：某消息的信息量越大，熵就越大；某事件发生的不确定性越高，熵就越大；某事件概率分布的分散性越大，熵就越大。

互信息量MI描述两个系统(图像)的统计相关性，常被用于医学影像的配准(比如，正常与不正常器官图像的配准)以及遥感图像配准。然而不同模式的图像配准会出现重叠效应等问题，多类形式的MI被提出来，如归一化互信息量、图像梯度互信息量以及区域互信息量(RMI)等。

真实SAR图像记为XR，仿真图像记为XS。两幅经配准的真实和仿真的熵及其联合熵为：

(5.1-16)

(5.1-17)

(www.xing528.com)

(5.1-18)

式中，pR(r)和pS(s)分别为XR以及XR中某灰度值出现的概率，pRS(r,s)是两幅图像相同位置的一对灰度值出现的概率，可由统计直方图直接求得。

互信息量的计算可表示为：

MI(XR,XS)=H(XR)+H(XS)-H(XR,XS)

(5.1-19)

较常用的归一化互信息量NMI(Särndal，1974)可表示为：

(5.1-20)

考虑到两幅相似图像具有相似的像元灰度分布和灰度变化方向，加入图像的梯度值和梯度方向可以减少互信息产生的全局最大值和差值引起的局部极小值。

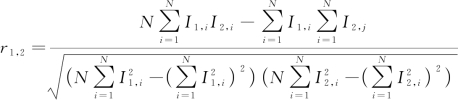
(5.1-21)

由于不同传感器的图像配准会有地理和散射差异，可使用互信息量进行多源图像配准。配准过程包括：①光学图像与SAR图像的粗配准；②真实SAR图像和仿真SAR图像的配准。前者为粗配准过程，确定建筑物中心的位置即可；后者为精配准过程，通过平移真实SAR图像XR，通过计算平移后的图像XR和仿真SAR图像XS的互信息量最大值确定：

(5.1-22)

式中，是MI取得最大值时的平移矢量。互信息量取最大值时两图像配准效果最好。