MRF框架下的区域合并准则优化

假定图像被分割为Q个区域，记为R1，R2，…，RQ；若假设Λ表示图像各区域所有可能的分类结果，即Λ={1,2,…,k}。观测影像f其特征场定义为F={Ft,t∈T}，其中Ft为区域Rt的协方差矩阵。标记场定义为X={Xt,t∈T}，其中Xt为区域Rt标记(Xt∈Λ)。根据最大后验准则(Maximum a Posteriori,MAP)，标记x的取值应使最大后验概率最大：

(4.5-4)

根据贝叶斯公式则上式可以重写为：

(4.5-5)

其中p(f|x)为区域类条件概率密度，先验概率p(x)可根据Hammersley-Clifford定理，采用只考虑二阶的多层逻辑模型，由Gibbs采样获得。

对式(4.5-5)两边取对数可以得到，并将式(4.5-4)代入其中可以得到：

(4.5-6)

其中V(i,j)为势函数，可定义为：

(4.5-7)

其中β一般设置为常数，如果β值设置过大，则会出现过分割的现象。因此本节对β的选择进行了改进：

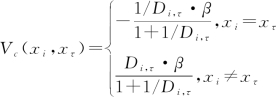
(4.5-8)

Di,τ为当前区域与领域之间的距离，可由如下公式进行计算：

(4.5-9)

从式(4.5-6)可以看出，需要对参数|Σm|进行估计，本节采用了EM算法对参数进行估计。

EM算法分为E步骤和M步骤，具体步骤如下：

(1)E-步骤。

假定N个样本集{C1,C2,…,CN}是独立的，同时其参数集为{Σ1,Σ2,…,ΣM}，其中M表示为分类的类别数。则其似然函数可定义如下：

(4.5-10)

其中：

(4.5-11)(www.xing528.com)

结合式(4.5-10)、式(4.5-11)，式(4.5-10)可重写为：

(4.5-12)

由于EM算法处理的是一种非完全数据，同时由于EM算法受初始值影响较大。本专著初始值设置为：

为属于ωj类像素个数)

(4.5-13)

(2)M-步骤。

最大化公式(4.5-10)，得到新的参数∑：

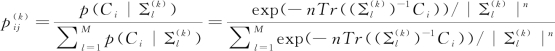
(4.5-14)

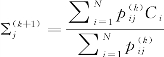
(4.5-15)

随着分类的迭代进行，根据式(4.5-14)、式(4.5-15)更新模型参数。

在式(4.5-6)中，为了平衡特征场和标记场的能量，引入一个加权因子连接二者：

(4.5-16)

本专著中采用的α的初始值为20，其中α(k)=α(0)·0.98k+1。k表示迭代次数。随着迭代进行，特征场能量减弱，标记场能量得以加强，二者共同作用分类结果。

综上所述，结合均值漂移与分层MRF场，本专著提出了一种新的非监督分类算法，其具体算法流程如图4.20所示。

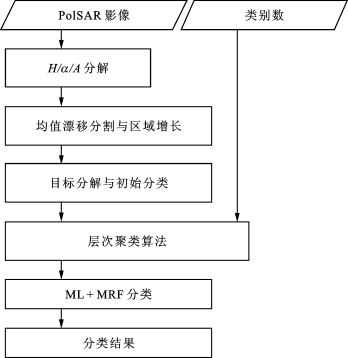
图4.20　算法具体流程

算法步骤如下：

1)通过H/α分解得到解得到极化特征向量，并将这3个极化特征量作为均值漂移过分割地输入特征向量。其具体公式如下:

(4.5-17)

2)采用Mean-Shift算法进行分割，得到过分割区域。采用Edison软件进行，将空域带宽设置为6.5，特征空间域带宽设置为7.5。如果分割区域过小，图像被分割成的区域数目过多，会导致后续的计算量变大，因此有必要对一些小区域进行合并。由区域增长模型(Region Growing Segmentation，RGS)进行区域合并，设置最小区域大小(一般设置为20)。

3)由 H/α/SPAN/A对区域进行初始类，共分为48类，由层次聚类算法对多余的类别进行合并。然后对初始分类结果进行统计，选择训练数据，对不同类别的参数进行统计，对初始分类结果采用基于最大似然准则下的Wishart聚类器进行迭代聚类(迭代次数一般需要2～4次)。

4)由步骤3)得到的初始分类结果作为区域MRF的初始分类结果，由Wishart分布对区域协方差矩阵进行建模，由EM算法进行参数估计，采用可变的权重连接标记场和特征场，由ICM算法求取基于最大后验下的分类结果。