均值漂移算法与区域增长的应用

均值漂移是一种有效的统计迭代算法，基本思想是通过迭代搜索特征空间中样本点最密集的区域,搜索点沿着样本点密度增加的方向收敛到局部密度极大值点。该算法由Fukunaga 等(1975)提出，经Cheng 等(1995)的拓展，在图像平滑、图像分割、目标跟踪等计算机视觉领域得到了成功的应用。其数学描述如下：

假设样本x 是d 维样本空间的总体X={xi|i=1,2,…,n}中的样本，则样本x概率密度函数的Parzen 窗估计为：

(4.5-1)

式中，k(·)称为剖面函数,h为带宽，CK为归一化参数。若对于x∈[0,)，k(·)的导数k′(·)存在，则定义：剖面函数g(·)≡-k′(·)，核函数G(·)≡CGg(‖·‖2)。则由公式(4.5-1)可得概率密度的梯度估计为：

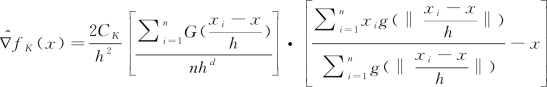
(4.5-2)(www.xing528.com)

其中可令：

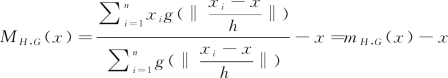
(4.5-3)

从上述式可以看出，第一个括号第一项是用G计算x 处的核密度估计，第二个MH,G(x)是均值漂移向量。一般mH,G(x)处的密度大于x处的密度，因此MH,G(x)总是指向密度梯度增加的方向。算法中可认为x 为均值漂移点当前位置，mH,G(x)为下一次迭代点，MH,G(x)就是两次均值漂移点间的运动矢量。当MH,G(x)大小为零或满足一定停止迭代准则时，均值漂移停止，收敛点为局部密度极大值点，也就是要寻找的密度的模式点。如图4.19所示,图4.19(a)为极化伪彩色图，图4.19(b)为均值漂移算法滤波后的结果图，从目视效果看，图4.19(a)受相干斑噪声影响较大，而图4.19(b)所受的影响较小，目视效果较好。图4.19(c)为经过均值漂移分割后得到的区域图，采用Edison软件进行分割，经分割后得到了一个个相互连通的区域。

图4.19　均值漂移分割结果图