高清成像技术中的合成孔径及压缩方位向

雷达测距只能得到距离向一维像，在方位向(飞行方向)只能靠天线窄波束来分辨不同位置的目标，由于目标远离雷达，天线波束再窄，方位向分辨率也无法达到理想水平。利用合成孔径技术，可等效地获得与合成孔径长度成反比的极窄波束，从而实现方位向的高分辨率成像，这就是合成孔径雷达(SAR)的原理。

如图3.2所示，平台朝方位向飞行的同时，天线朝距离向照射，照射区域的位置和大小由天线的方向图决定，照射区域的长度就是合成孔径的长度，宽度称为成像的条带宽度(Swath)。

所谓合成孔径技术就是将合成孔径内不同位置所接收的信号进行合成，最经典的实现方法就是利用多普勒率调制进行方位向压缩。

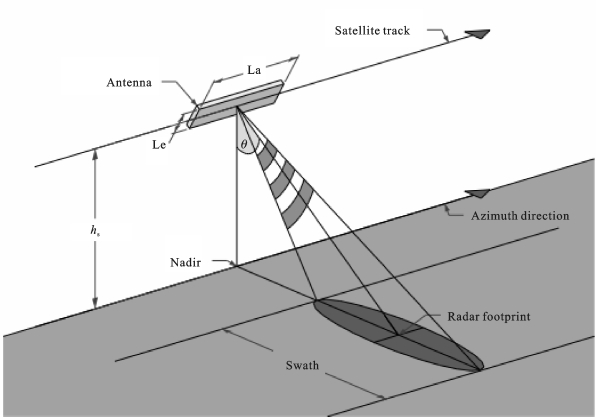
图3.2　侧视雷达成像系统

设雷达以速度v沿方位向飞行，以间隔Tr重复发送LFM矩形脉冲波，定义脉冲重复频率(Pulse Repeat Frequency，PRF)为1/Tr，雷达发射信号可写为：

(3.2-1)

设(x,r)处点目标的散射幅度为σ(x,r)，则该点的回波经过中频后可写为：

(3.2-2)

式中，ϖ表示为方向图增益，R(t)为目标离雷达距离。

首先对该回波信号进行距离向脉冲压缩，则距离向压缩后的信号为：

(3.2-3)

式中，δR[·]表示距离向压缩后的冲击函数，即幅度项。相对于电磁波传播而言，雷达飞行速度要慢得多，可假设在一个脉冲发射到接收期间雷达静止不动，这就是著名的一步一收(Stop-and-Hop)模型。则有：

(3.2-4)

式中，[·]表示取整。就是雷达发射脉冲的时刻,称为慢时间；快时间则定义在一个脉冲收发期间之内，即τ=t-nTr。

若将式(3.2-3)按快、慢时间排列为二维阵列，第一列表示第t个脉冲对应的回波，可重写为：

(3.2-5)

图3.3形象地表示了该信号的结构及其收集过程，重排以后同一目标的回波将按一条抛物线的轨迹排列，这是由于一个合成孔径内雷达到目标的距离变化引起的，这一效应也称为距离徙动(Rang Migration)效应，这一轨迹在n-τ平面上可表示为：(www.xing528.com)

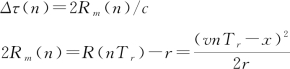
(3.2-6)

式中，Rm(n)称为距离徙动量。

令nxTr=(x/v)，则第一个脉冲发射时刻为距离目标最近的点，也即合成孔径的中心。设合成孔径长度为L，则包含在合成孔径内的脉冲时刻个数为：

(3.2-7)

只有在这些时刻目标才被照射到，这在方向图增益中体现，重写增益函数为：

(3.2-8)

式中，ϖ0(n,r)为仅与目标相对位置有关的方向图增益函数，理想情况下可认为照射区域内均匀辐射，则可以忽略方位向关联，即ϖ0(r)。

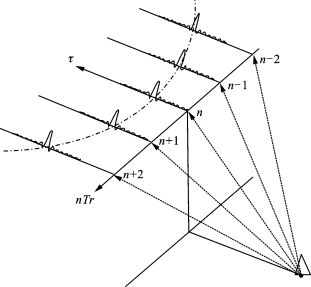
图3.3　一步一收模型与快慢时间重排

若将徙动轨迹上的s1信号峰值排列成一维信号，可写为：

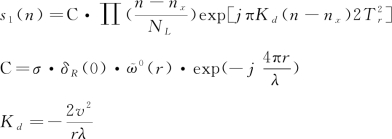
(3.2-9)

式中，C为常数，Kd为多普勒调频率。由于s1是一个LFM矩形脉冲回波信号，于是可采用脉冲压缩技术进行方位向压缩。其带宽也称为多普勒带宽，可写为：

(3.2-10)

对应时间分辨率为1/Bd，故方位向空间分辨率为：

(3.2-11)

可看出，方位向分辨率与合成孔径成反比，与距离和载波波长成正比。