建筑详图中的断面图制作技巧

尽管浮点数的表示和操作对于大多数工程师来说更直观，但浮点数的使用并非没有弊端。首先，浮点表示法可能超出必要的宽度，因此增加了系统花费和功耗。并且，整数硬件明显要比浮点硬件简单，因此可以实现更快的处理速度和更低的功耗。这些也是为什么高容量的便携式应用，尤其是手机，几乎从来不使用浮点DSP的原因。对于这些商品，市场环境决定了低成本和低功耗是主导因素。并且，在定点硬件上实现算法所需要的额外的编程复杂性，能够被大量的个体所分摊。对于一个宽度给定（如32位）的情况，定点数比浮点数（假定使用了合适的缩放比例）拥有更好的解决方案（因此有更低的本底噪声）。这是由于浮点数尾数的位数相比定点数要少所造成的。

定点表示法支持仅使用整数运算硬件来处理小数运算。定点数的二进制小数点被约定在补码的一个固定的位置。典型情况下，补码是一个16位的数值。二进制小数点的位置由Q-number计数法来指明，Qn是指约定有n位位于二进制小数点的右侧。最常用的是Q15和Q12格式，如下：

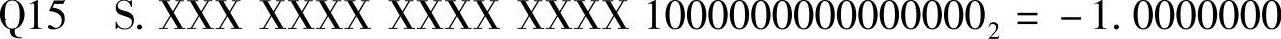
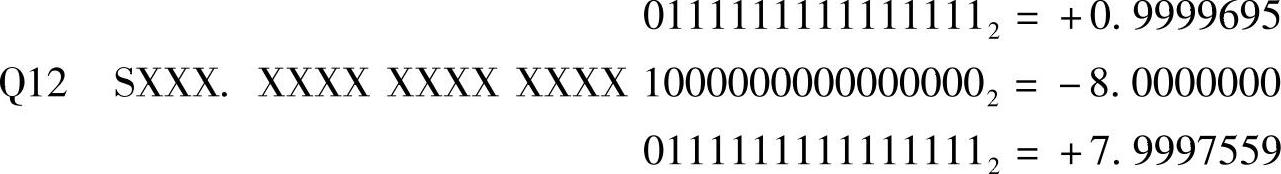
为了确定一个定点数的十进制数值，首先要确定是正数还是负数。符号位S为1表示负数，0表示正数。对于负数，要把它变换为对应的正数，也就是它的补码。最后，把每一位的值乘以对应的权再相加，就可以得到该数值。

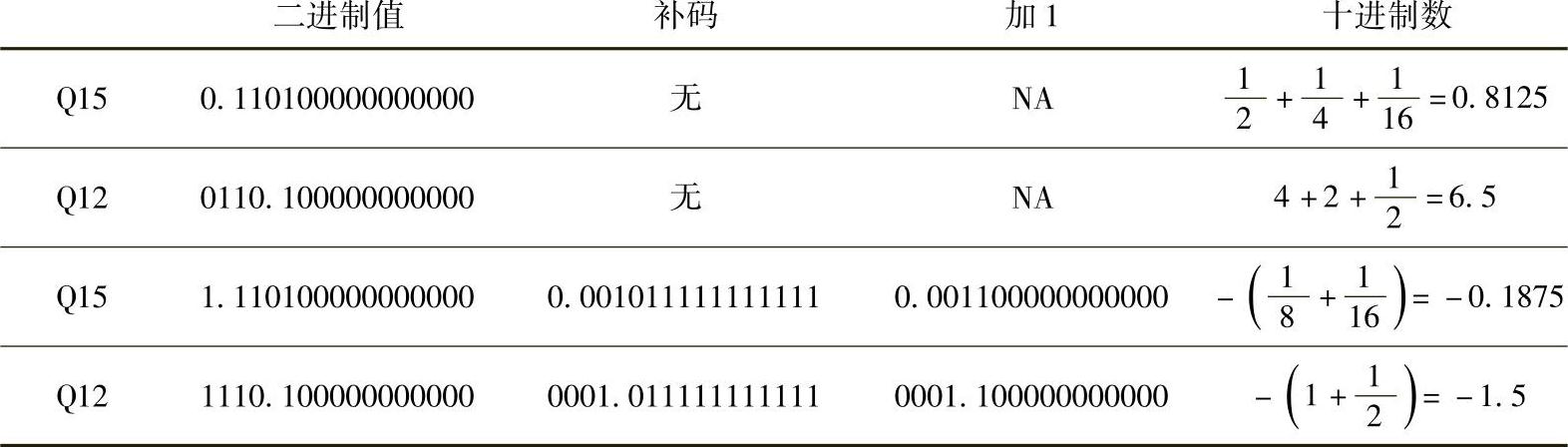
要注意的是，定点数运算要在标准补码整数运算硬件上实现，因此必须直接得到正确的结果，而无需对结果进行修正。对用整型逻辑进行的加法如下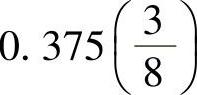和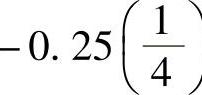的Q15数值应用整型逻辑进行的加法如下：(www.xing528.com)

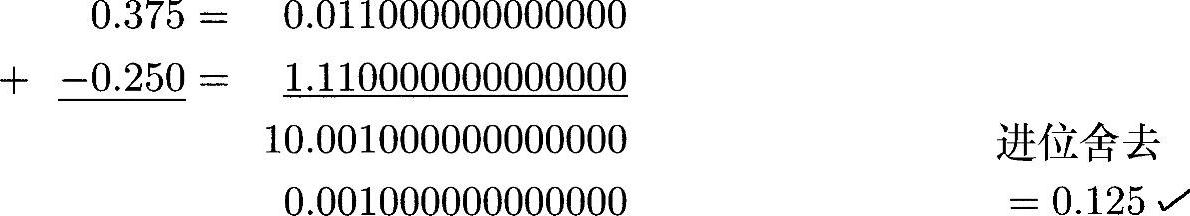
对两个n位数做二进制乘法，乘积有2n位。对两个Q15格式的数做乘法，乘积是一个32位的Q30格式的数，且有一个额外的符号位。要把乘积变回Q15格式，需要将其右移15位并且长度截断为只有16位。注意，负数乘法需要不同的算法，这里不再进行说明。

有一点很有用，在浮点数中，指数支持自动比例缩放，而对于定点数，运算中需要设定比例以防溢出。通常情况下，在信号处理中使用Q15格式，因为除了

（-1）×（-1）的异常情况，两个Q15数的乘法绝对不会溢出Q15数的表示范围。