C.4浮点表示法

在浮点表示法中，数值包括尾数和指数两部分，就像我们通常使用的科学计数法一样。不过，与（尾数₁₀×10^指数10）的形式不同，浮点数是以二进制的形式（尾数₂×10^指数2）存储。一般地，浮点表示法可以使用IEEE单精度和双精度格式[70]，如图C.1所示。

图C.1 IEEE-754中浮点的表示

下面详细讨论一下单精度表示法，双精度表示法从概念上讲比较相似。在单精度表示法中，符号位代表了该数值的符号，0代表正数，1代表负数，可以解释为-1^S。该数值的8位指数部分的偏移量为127（称为“余127”），这样000000002表示-127，111111112（25510）表示128，011111112（12710）表示0。因此，指数因子的取值范围是2^-127～2¹²⁸，不过我们稍后会看到一些特殊情况下的指数保留值。23位的尾数部分为二进制数值1.MMM…MMM，注意是二进制小数，而不是十进制小数。尾数的每一位所代表的数值如下：

通过约定最高位为1（归一化条件下），尾数的范围可以从（1.0）（当所有的M位都为0时）到（2.0-2^-23）（当所有的M位都为1）。浮点数的样本如下：

最后一个，尽管该浮点数很接近0.1，但使用这样的形式，不可能精确表示0.1。实际上，0.1可以由一个无限的二进制序列来精确表示。

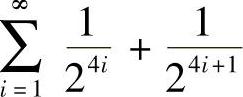
并且，使用它来计算是不准确的。尽管误差可能相当微小，但经过重复计算，可能会导致相当大的累积误差，并且一种形式的量化噪声也会存在于结果中。

如果尾数的最高位约定为1，就不可能精确表示0.0。为了解决这个问题，专门为精确表示0.0指定了一种方式。如果指数和尾数域都是0，IEEE标准定义该值为0.0。

尽管浮点表示法允许更宽的数值范围，在数学计算中依然可能存在其他不准确性。一种可能导致不准确的情况是，把一个很小的数加到一个非常大的数上时。为了加或减两个浮点数，必须要先将它们变换为具有相同的指数值的形式，然后尾数才能相加。加完尾数后，和要进行归一化，尾数的最高有效位应为1，然后调整指数。如果两个数中，一个比另一个大太多，结果可能会不准确。我们用下面的图来表示两个加数。(www.xing528.com)

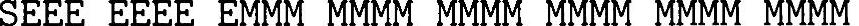
操作数1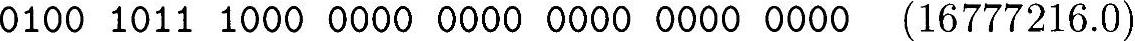操作数2

把第二个加数的指数变换为第一个加数的指数151（100000002）后，尾数的加法会发生下面的情况（指数没有显示）。

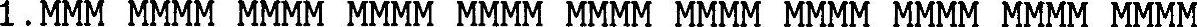
尾数1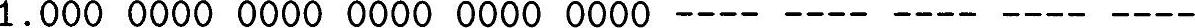

尾数2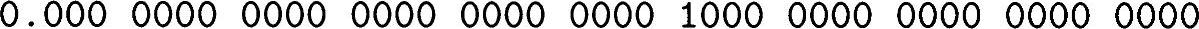

和

和的尾数

为了便于存储，和的尾数必须要被截断为23位。当这样处理之后，我们可以看到和的尾数与第一个加数的尾数相比没有变化，加法没有起作用。更详细的关于计算中数值准确性讨论见参考文献[71，72]。

除了存储归一化数值外，IEEE浮点标准还规定了一些特殊的表示方式，用以表达非标准化数值，以及各种非法数值和错误情况，比如NaN（非数值）。详细讨论参见参考文献[70]。