程序清单15.1：PLL的仿真
程序清单15.1的解释如下。
（1）第5行：定义一个系统的载波频率为12kHz。
（2）第6、7行：定义载波频率和相位的误差。这些误差将加入到仿真中。
（3）第8行：定义系统的采样频率为48kHz。这个采样频率和DSK音频编码的速率是相互匹配的。
（4）第9行：定义仿真中的采样总数。
（5）第10、11行：结合系统的采样频率，这部分代码行指定符号的速率。在二进制相移键控（BPSK）仿真中，这个符号速率和比特率是相同的。要非常强调的是，必须满足奈奎斯特（Nyquist）采样定理的要求。这个要求强调你必须足够快地进行采样以避免输入信号的失真。如果我们实现BPSK信号是使用12kHz的载波信号和一个双极的脉冲序列相乘得到的，因为理想双极脉冲的带宽是无限的，必然会有所失真。
（6）第12、13行：指定和环路滤波器相关的滤波器系数。
（7）第14行：与第16、17行一样，对系统仿真加入一定的噪声。
（8）第16行：一个16位的ADC和DAC的完全范围是+32767～-32768。这个幅度的归一化因子使得输入信号接近允许但不超过ADC的最大范围。
（9）第17行：对相位误差信号反馈进入相位累加器之前进行归一化。因为PLL驱动系统的相位误差接近0，我们希望这个相位误差是一个非常小的数（一个小的弧度数）。
（10）第19、26行：创建一些变量来仿真PLL的每个采样的处理过程。保存一个矢量而不是只当前最近的数值，这样可以高效率地产生相关的图形。
（11）第31、32行。与环路滤波器中单个等效的IIR滤波器实现相关联的系数。这可以通过简单的仿真来确定。在参考文献[64，65]中，环路滤波器是通过并行的形式来实现的，如图15.2所示。
（12）第37、38行：创建一个BPSK基带信号。
（13）第41行：把BPSK基带信号和载波信号进行混频，并加入一些噪声。
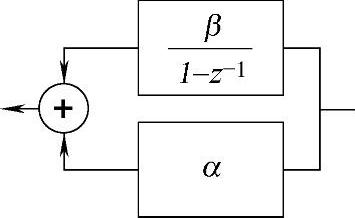
图15.2 环路滤波器 并行实现框图
（14）第42行：计算输入信号“s[n]”的分析信号的输出，幸好Matlab定义通过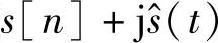
来定义一个解析的信号。这种定义我们在前面有所介绍。在这里我们必须注意“analyticSignal”信号是一个复数。
（15）第46行：计算第一个混频器的输出。
（16）第47行：计算信息信号的估计。(www.xing528.com)
（17）第48、49行：对第二个混频器进行计算并归一化。
（18）第50行：执行环路滤波器的操作。
（19）第51行：将滤波器的最后设置保存到滤波器的起始设置变量，从而保存滤波器的状态。
（20）第52、53行：在相位累加器中计算下一个数值。mod命令保持相位累加器的输出在0～2m的范围内。
（21）第54行：计算本振（LO）的输出数值。一个复指数形式可以使用欧拉公式[8]来当作一个正弦项和一个余弦项。
仿真结果的图形输出虽然没有在程序中出现，但是可以使得我们更详细地了解PLL。由于仿真可以随机地初始化本振的频率和相位误差，并且加入到信号的噪声是随机的，仿真的行为将随着每次运行仿真而不同。可以通过在每次仿真的开始重新初始化Matlab随机数发生器的状态或者设定第16、17、24行的变量等于0，来控制这个随机的过程。Matlab随机数发生器的状态可以通过Matlab命令randn（′state′，0）来重置。
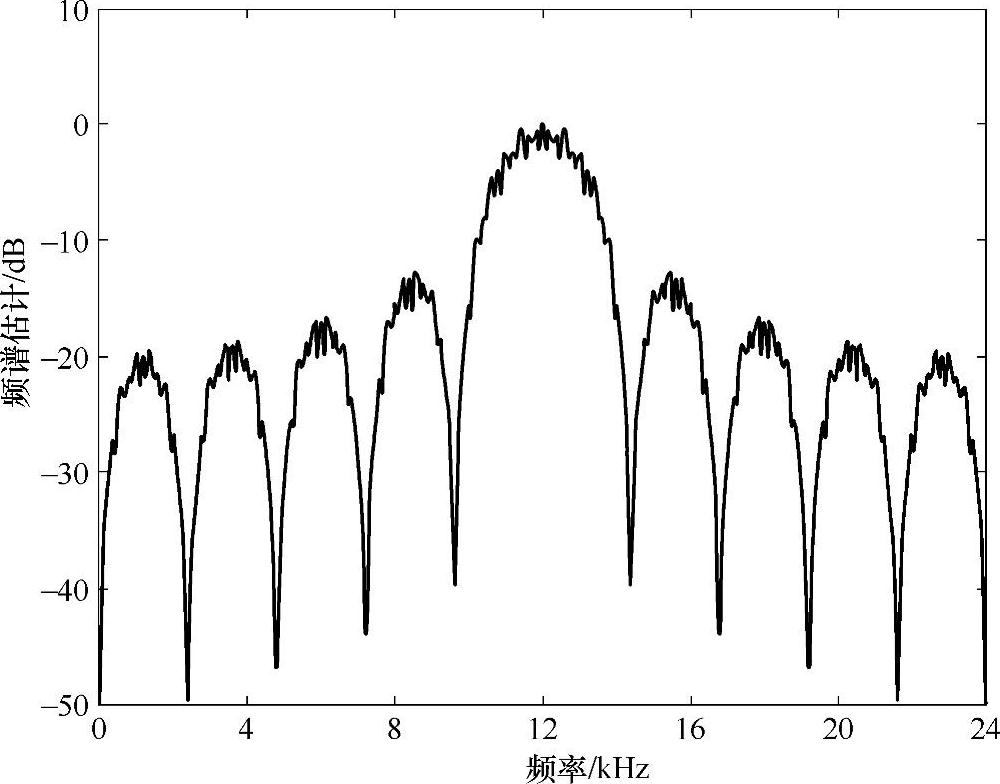
图15.3 BPSK信息符号和12kHz载波混频输出的归一化频谱估计
BPSK信息符号和12kHz载波混频输出的归一化频谱估计如图15.3所示。这个环路滤波器的零点/极点图如图15.4所示。在这个图中，极点位于单位圆上，虽然从图15.5上看不清楚，但是确实导致0Hz处无限大的增益。PLL的正确的起始瞬态输出如图15.6所示。虽然这个行为非常常见。2阶Costas环路对于180°相位转换失效，系统的输出如图15.7所示。在图15.7中，这个恢复的信号和原始的信息信号相比相位差为180°。这种信号误差是灾难性的（例如，BPSK通信系统将导致100%的比特恢复误差）[9]。假设我们使用二进制补码的数值表示，反转所有比特的状态只引发符号的变化，最后一个非常大的频率误差加入到本振，这会在PLL开
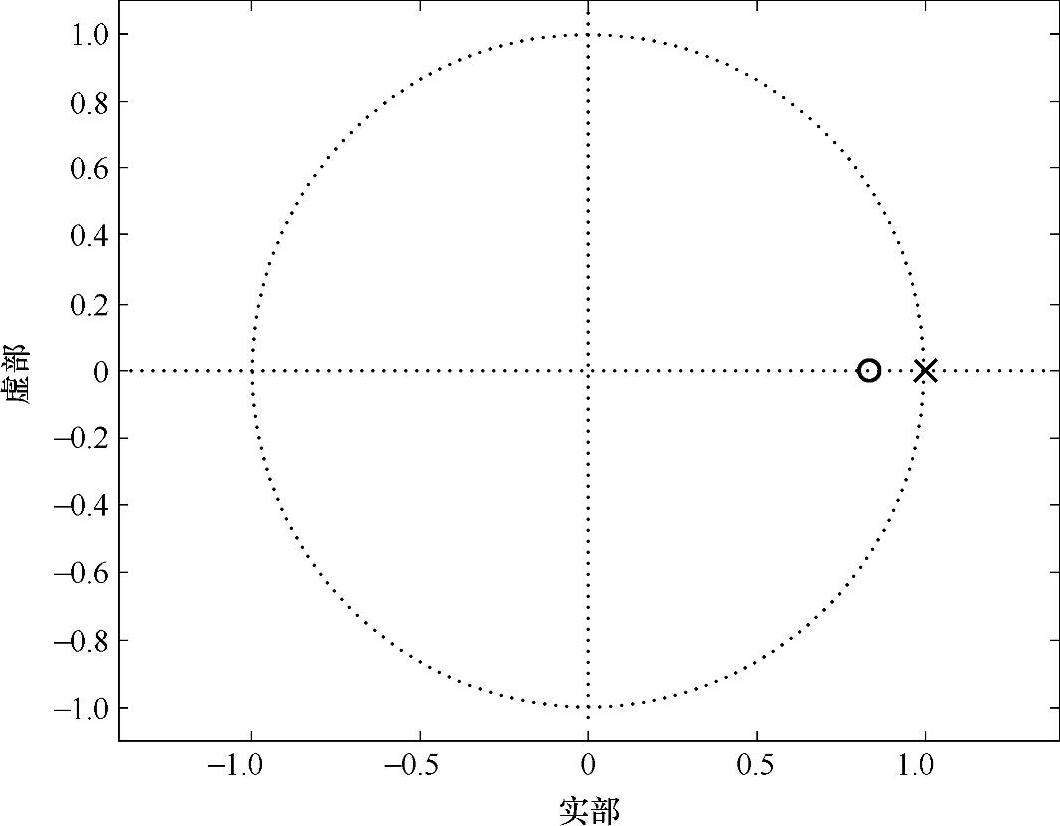
图15.4 环路滤波器的零点/极点图
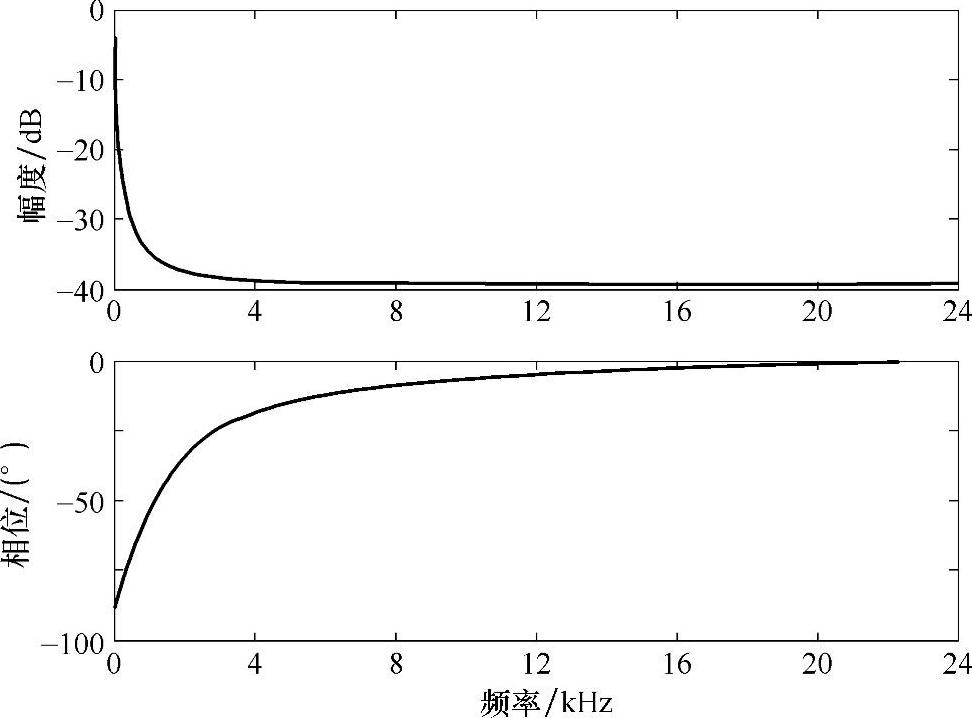
图15.5 环路滤波器的频率响应
始阶段引入非常长的瞬态延时。如图15.8所示，需要300～500个采样周期来使得PLL稳定跟踪输入的信号。在这个仿真中，这是20个采样/符号。这相当于在PLL稳定之前15～25个符号的信息无法得以恢复。根据通信系统使用的场合不同，这个PLL的瞬态的行为可能是灾难性的或者无关紧要的。
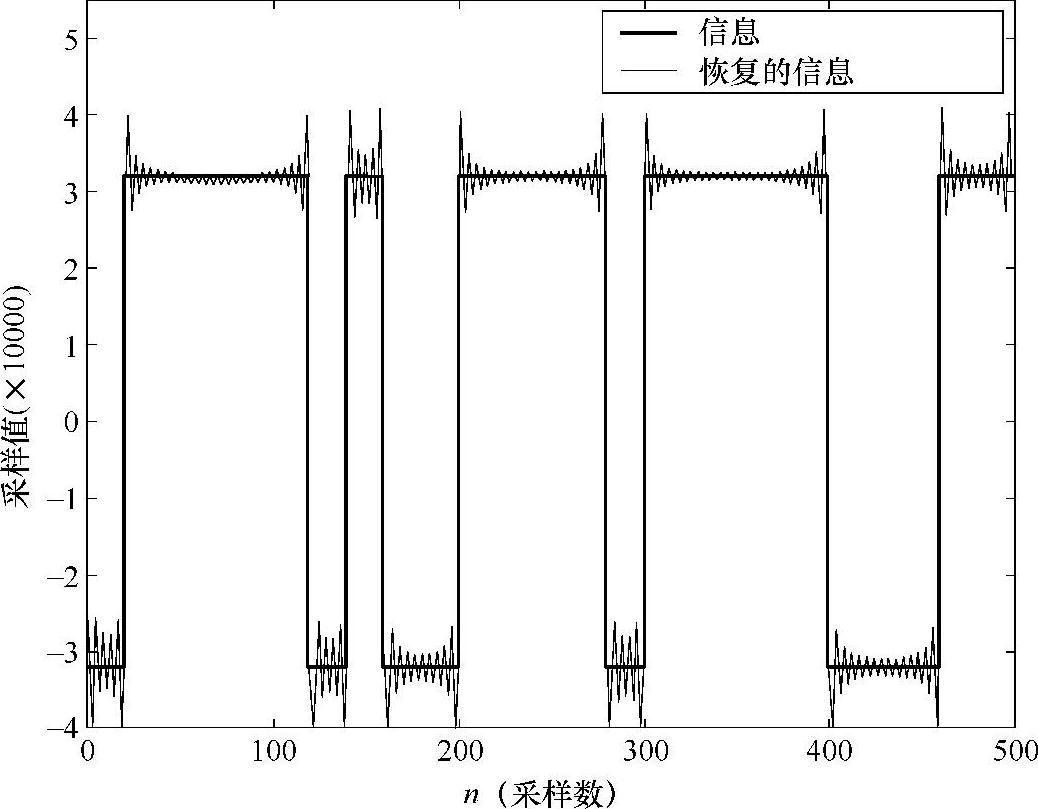
图15.6 PLL的开始阶段的正确的瞬态行为
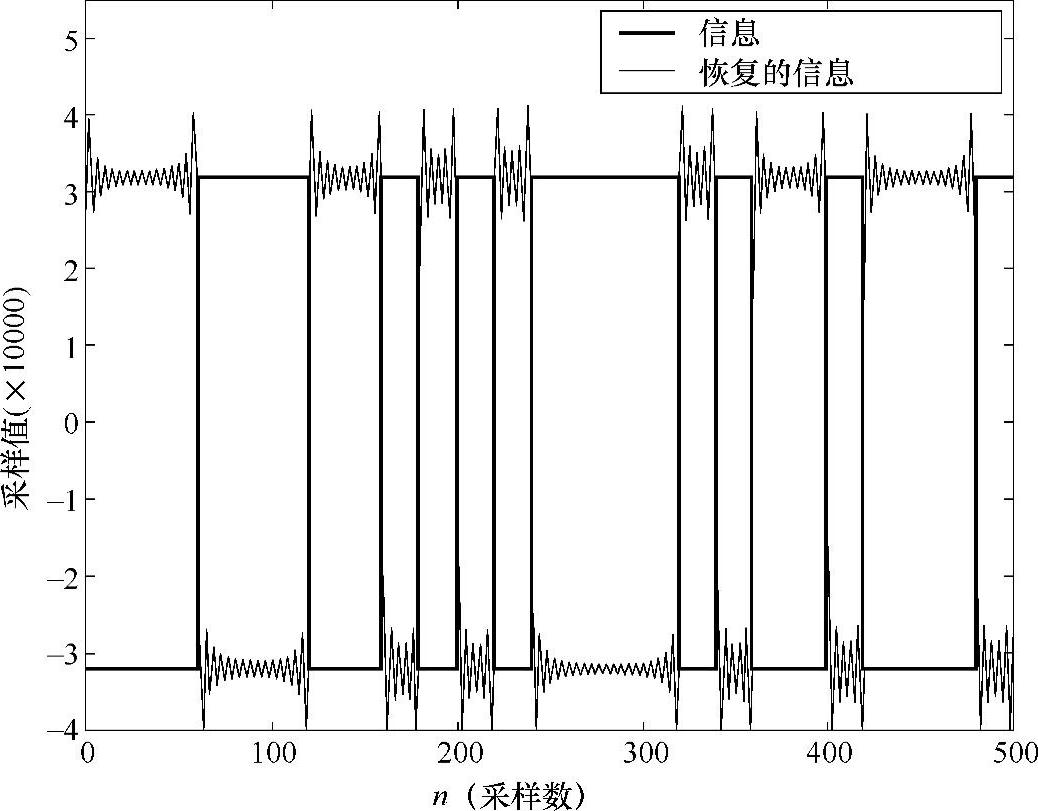
图15.7 具有180°相位误差的PLL起始阶段正确的瞬态波形
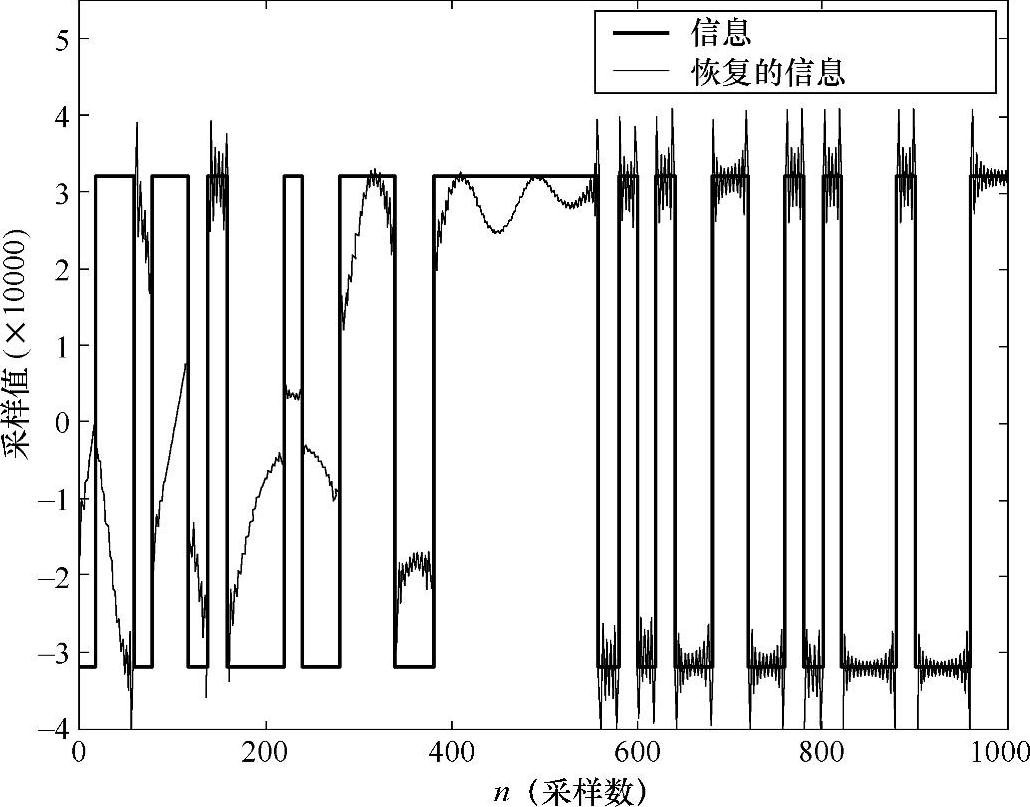
图15.8 更扩展的PLL起始阶段瞬态波形
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
