锁相环基础原理及实现简介

锁相环广泛使用于当前的通信系统中。可以查到很多关于锁相环基础理论的文献。这里，我们只是简要地进行讨论，然后实现一个单一的锁相环的设计——一个离散的2阶Costas环路^[64，65]。这个系统的一个简化的框图如图15.1所示。图中，s[n]是采样的输入信号，m[n]是信息信号的估计，T是采样周期，ω_c是载波的频率。

PLL的基本工作原理解释如下。输入的信号s[n]通过一个实现Hilbert变换（HT）的滤波器来创建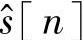。正如本书第14章我们提到的，HT操作的幅频响应是1（除了在0Hz处为0以外），对于正频率引入-90°的相移，对于负频率引入+90°的相移。如果一个信号可以表示成它与它Hilbert变换结果乘以虚数单位j（j=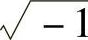）的和的形式，就称它是解析的信号。回忆一下jx=|x|∠90°，所以乘以j相当于对所有的频率成分进行+90°相移。注意，你还需要考虑HT滤波器操作的群延时来对准信号，正如在本书第14章所做的。分析的函数可以用方程的形式定义为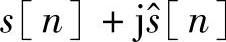。这就是为什么使用实线和虚线来表明框图中处理实数和虚数信号的部分。后面要做的是去除载波信号。

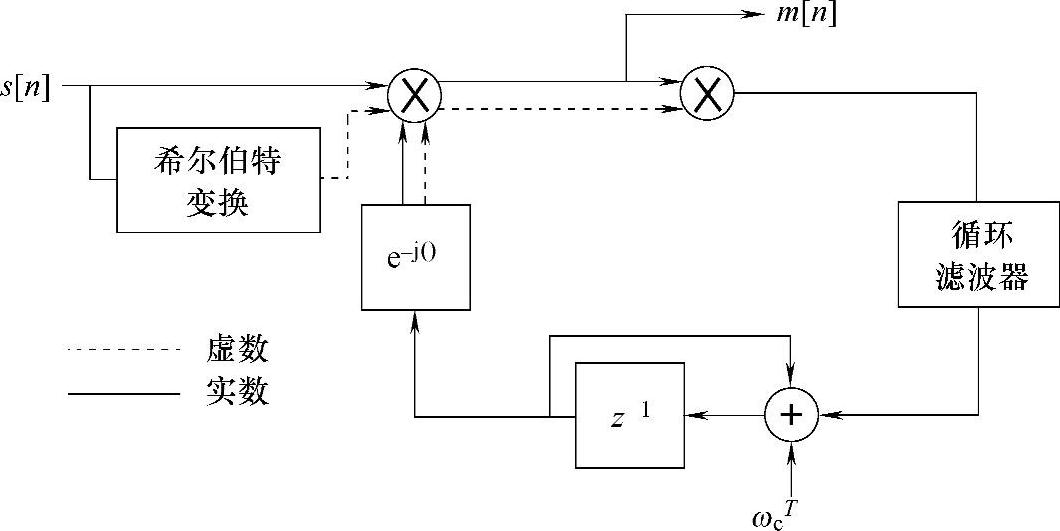
图15.12 阶Costas环路的简化框图

图15.1所示框图中的第一个乘积实际上是一个鉴相器的近似。更具体地说，指数模块e^-j（）的输出是一个正弦和余弦的波形。理想的情况下和输入的载波信号的频率和相位是相同的。这个复数的振荡器在模拟电路中成为本振（Local Oscilla-tor，LO）。乘法器的输出，也可称为混频器，包含信号和本振相位误差的近似。(www.xing528.com)

许多种幅度调制通信信号的正交解调，可以通过混频器输出的实部来恢复原始的信号m[n]。需要一个额外的滤波器来恢复一个更精确的传输信号的估计。二进制相移键控（Binary Phase-Shift Keying，BPSK），或者更通用的M-PSK，正交幅度调制（Quadrature Amplitude Modulation，QAM）可以看做是一种特殊的AM。更多相关的课题可以在本书第16章和第17章中找到。

第一个混频器的实部和虚部的输出是环路滤波器的输入。这个滤波器实际上是一个低通滤波器，它只允许一个本振相位误差反馈回复数振荡器。单个输入到复数振荡器（作为LO）的输入是两个相位累加器的输出。这个累加器将对振荡器的现有的相位加入一个相位增量ω_cT，然后这个相位误差的估计输入到环路滤波器。这个复数的振荡器和相位累加器一起一般被称为压控振荡器（Voltage-Controlled Oscillator，VCO）。

如果本振（LO）的工作频率非常接近输入载波的频率，这个PLL将能够立即去除它们的频率和相位误差。这就是PLL得名的原因。相位误差反馈环路可以在不影响系统的前提下快速地完成这个锁相的任务。