基于Hilbert的AM接收机从接收到的信号中提取真实的包络[63]是基于下面的方程:
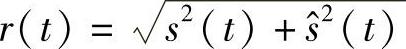
在这个方程中r(t)是AM信号的真实的包络。这个包络可以被表达为r(t)=m(t)+DC,其中m(t)是信息信号,“DC”表示加入到AM接收机中的直流偏置,它将保证m(t)+DC>0。另外,s(t)是接收到的AM信号,s^(t)是这个信号的Hilbert变换。一旦提取了真实的包络信号,通过基于IIR的隔直流滤波器来去除其中的直流项。
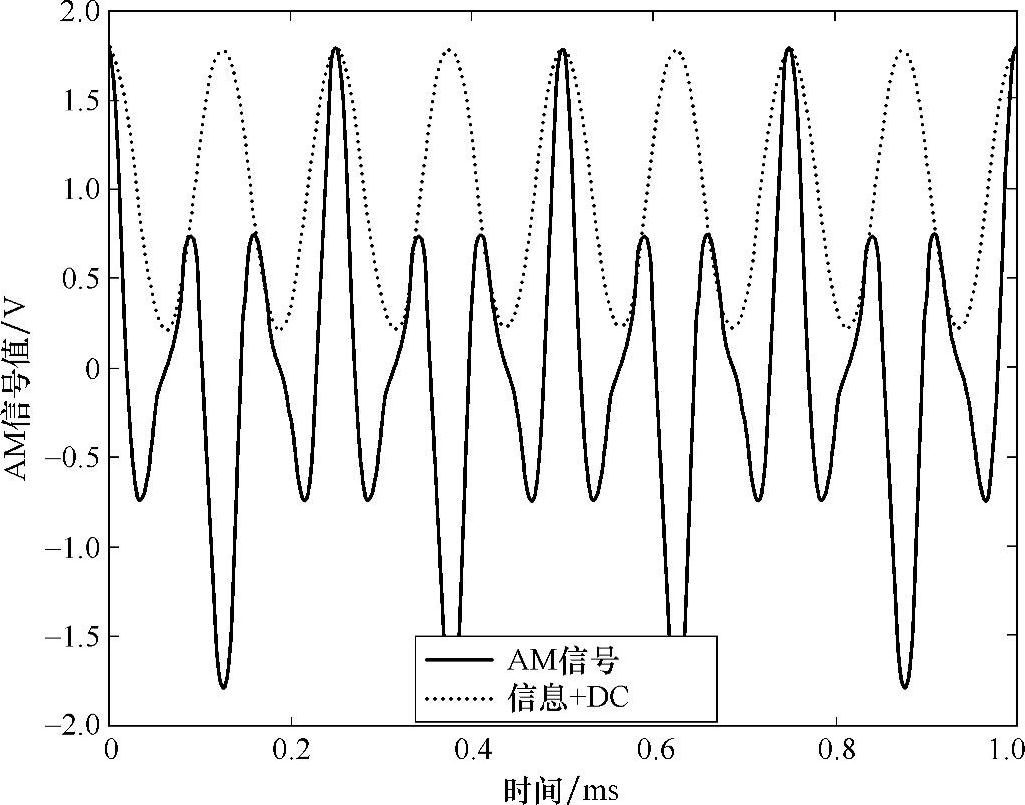
图14.10 AM波形(fmsg=8kHz,fc=12kHz)
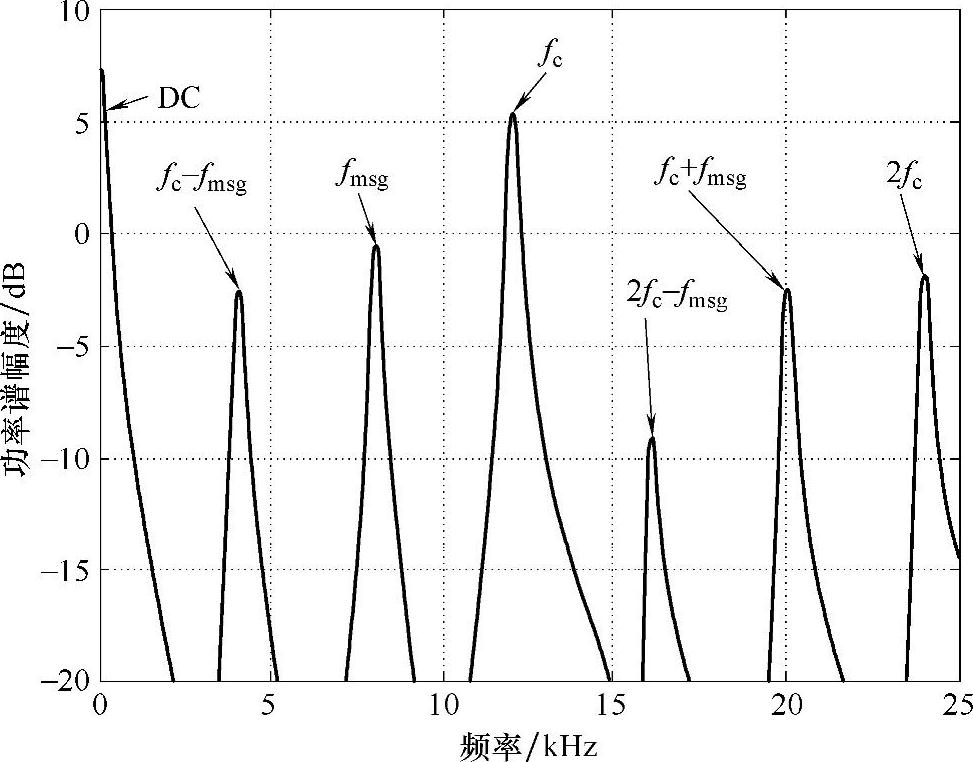
图14.11 AM频谱(fmsg=8kHz,fc=12kHz)
为了创建s^(t),必须使得s(t)通过一个Hilbert变换的系统。一个连续时间的Hilbert变换滤波器的单位脉冲响应定义为
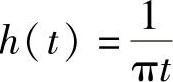
它的频率响应定义为
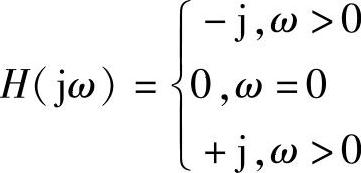
这个频率响应的幅度为1(除了只在0Hz处为0),对于正的频率滤波器引入-90°相移,对于负的频率滤波器引入+90°的相移。这个相移滤波器可以通过一个FIR数字滤波器来实现或者通过FFT/相移/IFFT的操作来实现。本章我们使用一个基于FIR滤波器的方法来近似Hilbert变换。
为了使用Matlab设计一个基于FIR的Hilbert变换滤波器,我们使用remez命令[6]。下面的例子显示了如何使用这个命令。
程序清单14.1;使用Matlab设计一个Hilbert变换滤波器
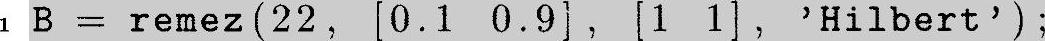
 (https://www.xing528.com)
(https://www.xing528.com)
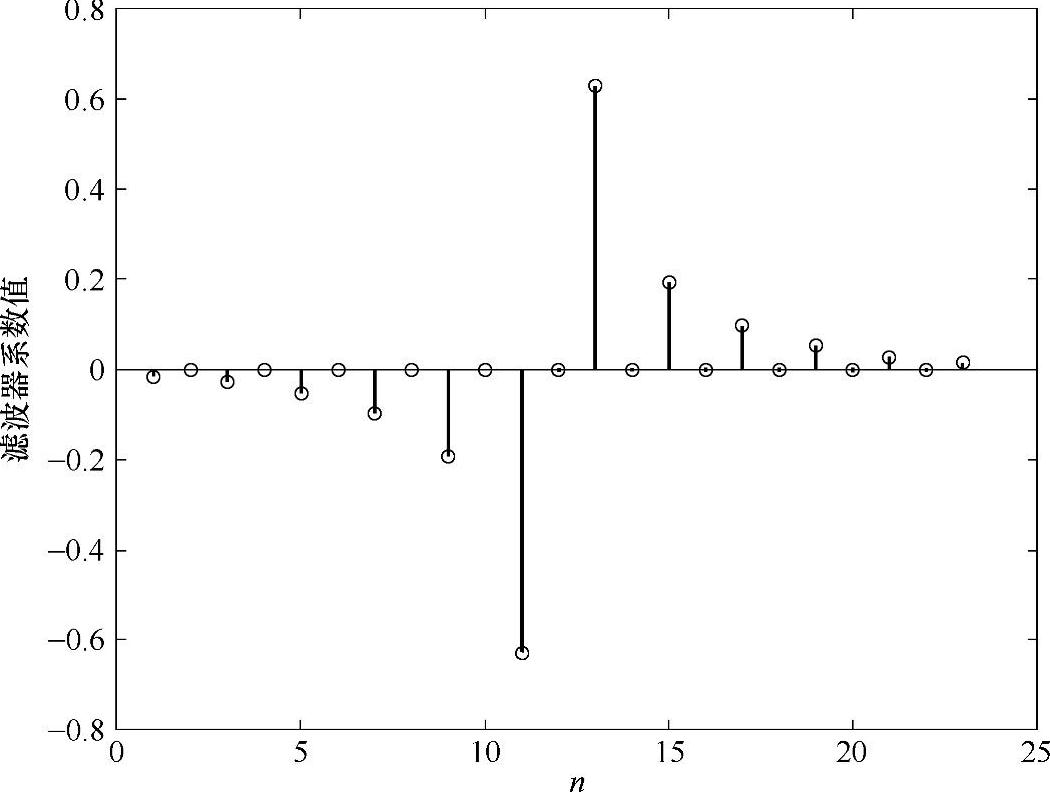
图14.12 22阶FIR Hilbert变换滤波器系数的棍图
在这个程序中,变量“B”存储了23个滤波器的系数;滤波器的阶数是22;0.1和0.9是归一化频率的开始和截止频率,在这之间的频率范围我们希望获得幅频响应为常数。“[11]”表示在这两个归一化频率处的幅度,“Hilbert”告诉Matlab软件中设计了一个Hilbert变换滤波器。存储计算结果的系数“B”的棍图如图14.12所示。我们注意到这里的Hilbert变换滤波器具有归一化频率域上的一个对称的带宽,中心频率位于FS/4,我们看到滤波器的系数中每隔一个出现一个0。这个滤波器的系数是关于中心点奇对称的。这些特点可以用来减少DSP CUP[7]的计算量。
指定Hilbert的设计参数和你想变换的信号的特点紧密相关。图14.13所示为阶数逐渐提高的3个不同的滤波器。每个滤波器具有相同的带宽要求。对于给定的频率范围,更高的阶数,可以获得通带中更为平坦的特性。从图14.14所示曲线可以看到随着滤波器阶数的提高,滤波器的纹波逐渐减少,但是这个纹波是不可能完全避免的。
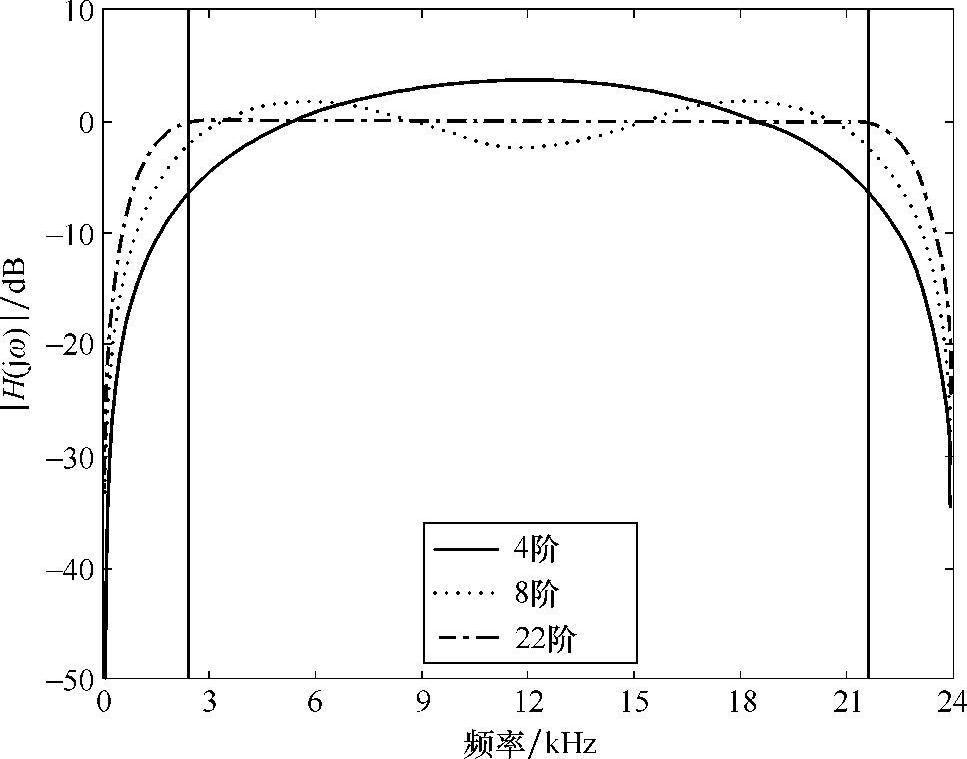
图14.13 3个Hilbert变换滤波器的幅度响应图
一个采样(离散)系统可以用s[n]和r[n]来代替包络提取方程中的s(t)和r(t)。与提取实际包络信号相关的框图如图14.15所示。我们注意到需要对未滤波的信号延时一个滤波器的群延时,以便未滤波的信号s[n]和滤波后的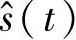 是对齐的。这个群延时是与线性相位的FIR滤波器相关的(例如Hilbert变换滤波器),它等于滤波器阶数的1/2。对于一个22阶的滤波器的例子,群延时是11个采样时间。因为输入信号到这个滤波器已经通过使用直接Ⅰ型(DF-Ⅰ)技术来存储,不需要额外的输出采样缓冲器来延时s[n]信号。
是对齐的。这个群延时是与线性相位的FIR滤波器相关的(例如Hilbert变换滤波器),它等于滤波器阶数的1/2。对于一个22阶的滤波器的例子,群延时是11个采样时间。因为输入信号到这个滤波器已经通过使用直接Ⅰ型(DF-Ⅰ)技术来存储,不需要额外的输出采样缓冲器来延时s[n]信号。
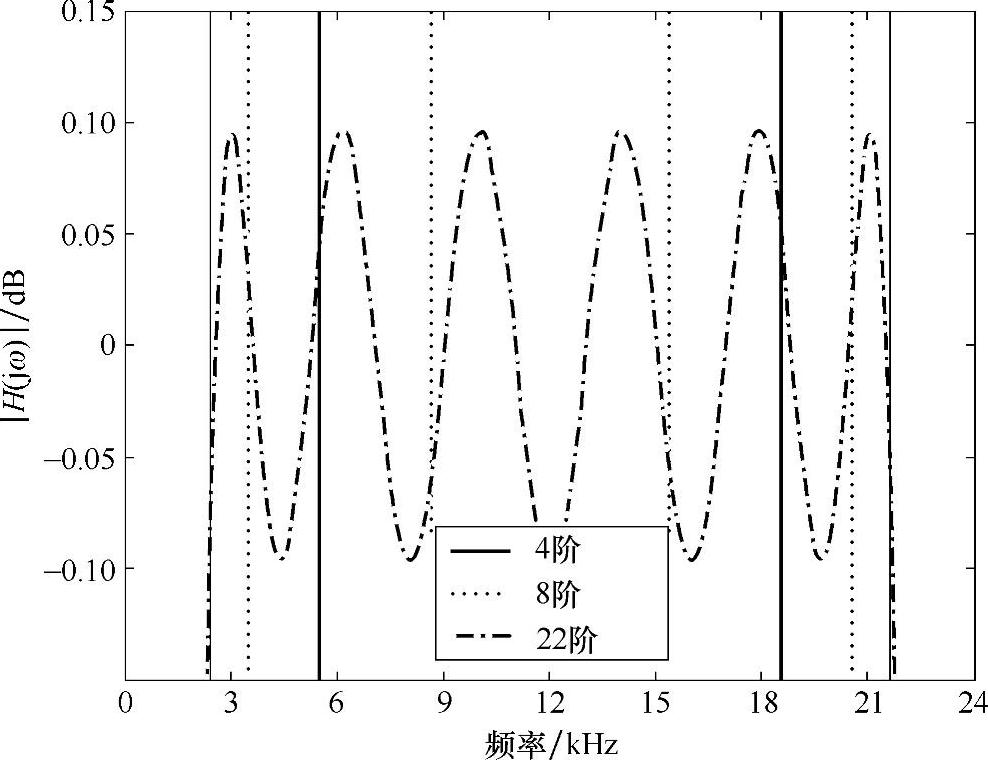
图14.14 22阶Hilbert变换滤波器的频率响应的放大图(可以清晰显示通带纹波)
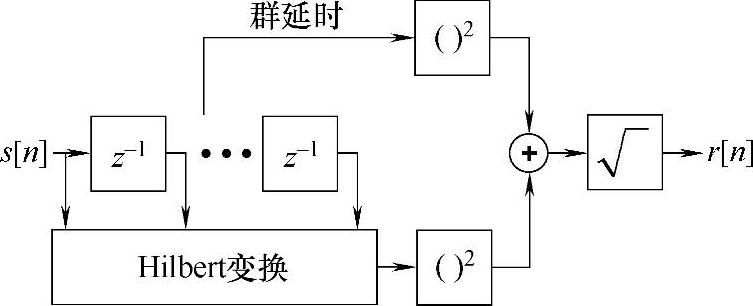
图14.15 AM信号的真实包络检波原理图
最后,r[n]必须去除相关的直流成分。这是通过一个陷波滤波器来实现的,它的阻带频率设定为0Hz。这个滤波器将零点位于单位圆的z=1的位置,这个零点决定了阻带的带宽,一个基点位于实数轴上且非常接近于零点(z=0.95)。这使得阻带的边缘非常陡峭。这个系统的传输函数如下:
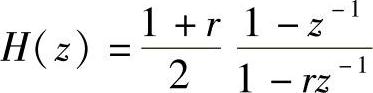
在这个方程中,r表示极点的位置(我们前面是用的例子中r=0.95),(1+r)/2项对高频(通带)增益归一化到1(0dB)。和这个系统相关的差分方程可以推导如下:
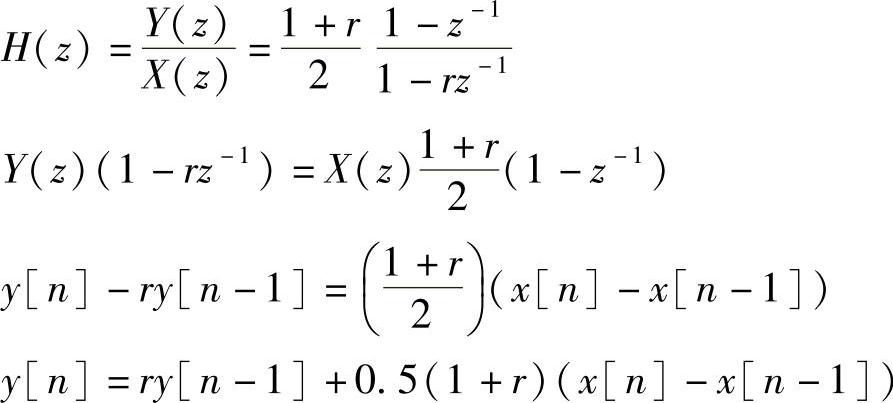
现在我们已经有足够的资料来实现如图14.15所示的一个AM解调器。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




