周期信号在DSP中的应用

周期信号有一个基本时间循环，通常被叫做周期。在这个周期中整个信号都确定了，接下来每一个周期都是重复的。对于连续时间信号来说，为完整定义这个信号，基本周期T₀是最少的时间要求；我们将看到与之关联的基本频率是f₀=1/T₀。一个周期信号可以包含多种频率而不仅仅是单一的基本频率。最简单的周期信号是正弦信号，因为它只包含了一个单一的频率。用这个正弦波形做例子，基本周期的概念意味着这个正弦必须符合这个等式

sin（2πf₀t+ϕ）=sin（2πf₀t+2πf₀T₀+ϕ）=sin（2πf₀（t+T₀）+ϕ）式中f₀为正弦信号的频率（Hz）；t为时间（s）；ϕ为某一任意的相位（rad）；T₀为周期^[15]。对于T₀来说和2π弧度的全周期的关系为，2πf₀T₀≡2π。这意味着，如我们前面论述的一样，f₀=1/T₀。注意，T₀必须是正数且为实数。这些看起来好像是没有意义的讨论，当从连续时间转换到离散时间表示时证明是很有用的。

对于我们正弦波形的一个离散时间版本，间隔T_S采样一次（T_S=1/F_S），并且我们用nT_S来代替变量t，这里n=0，1，2，…。这样我们获得了许多采样值。一个离散时间信号的周期N将用单位采样表示，并且就我们的正弦波形例子来说必

须符合下面的等式

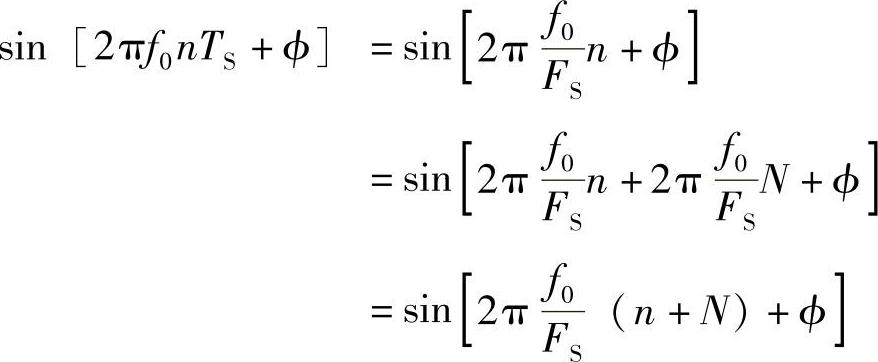
式中2π（f₀/F_S）为归一化的离散角频率（弧度/采样频率）。如果这个离散时间信号是周期的，那么对于某一个整数N在采样点n处的值一定等于在采样点n+N处的值。这意味着2π（f₀/F_S）N≡2πk，其中k是另一个任意整数。重新排列这个等式结果为(www.xing528.com)

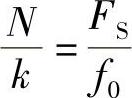
因为N和k都是整数，这个比值F_S/f₀必定是有理数，对于离散时间信号来说是周期的。换句话说，如果没有N和k的整数值解这一等式，那么信号的采样形式就不是周期性的。采样处理导致许多时间连续的周期性信号不能产生周期性的离散时间信号。

定义一个离散时间信号的信息不是必须惟一的，我们能够定义一个周期性信号在任何一点开始。图5.1所示为1kHz正弦信号的连续时间和离散时间的部分波形图，可以帮助理解这个概念。图5.1a所示为连续时间正弦信号，水平轴（时间轴）标示在图的上部。另外，周期（T=1ms）也标示出来。为计算采样周期，我们必须计算时间的离散时间表示为

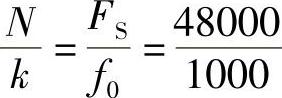
显而易见的结果是N=48和k=1。图5.1b所示为1kHz正弦信号（F_S=48kHz）的离散时间（采样）表示起始的48个采样点（即n=0，1，2，…，47），从t=0开始。了解图5.1b接下来的采样非常重要，这里N=47，不等于在n=0处的值。下一个采样（在n=48处）将等于n=0处的值。如果提供一个完整的离散时间周期，通过在选定的周期中复制这信号能够使这个信号成为“连续的”。这个概念的演示如图5.1c所示，这里48个连续的采样点被复制并被连接在一起成为两个完整的周期。重复这个连接处理将允许你产生任意长度形式的信号。图5.1d～f的例子是同一个信号，这个信号被定义的起始采样处理位置在n=20、30、40的采样点位置，各自给出了信号接下来的N=48个采样点。